Disjoint Set Union
Problem One : 维护区间连通块
F - Range Connect MST (atcoder.jp)
暴力模拟的话,就是基于 Kruskal 的思想,按 c c c 从小到大排序,对于每次询问,枚举检查 j ∈ [ l , r ] j\in [l,r] j∈[l,r] ,只要 j j j 与 n + i n+i n+i 不连通,就连一条边。
我们用并查集优化,并查集维护 1 ∼ n 1\sim n 1∼n 这些点,把他们维护为一个连通分量,祖先节点为最右边的节点,这样对于每次询问,对于 [ l , r ] [l,r] [l,r] 的每个连通分量,跟 n + i n+i n+i 连边即可,最后把他们全部 merge 起来。
O ( Q ( log Q + α ( N ) ) O(Q(\log Q+\alpha(N)) O(Q(logQ+α(N)) 。
tips :
DSU(Disjoint Set Union) 的时间复杂度通常被表示为 O(α(N)),其中 α 是阿克曼函数的反函数。阿克曼函数 A(m,n) 是一个非常快增长的函数,而它的反函数 α(N) 增长得非常缓慢,几乎可以认为是常数。
#include<bits/stdc++.h>
using namespace std;
#define int long longint const N = 2e5 + 10;int n, q;
struct info{int l, r, c;bool operator < (const info &T) const{return c < T.c;}
}infos[N];int p[N];
int find(int x){if(x == p[x]) return x;return p[x] = find(p[x]);
}
void merge(int x, int y){x = find(x), y = find(y);if(x != y) p[x] = y;
}
void solve(){cin >> n >> q;for(int i = 1; i <= n; i ++){p[i] = i;}for(int i = 1; i <= q; i ++){int l, r, c;cin >> l >> r >> c;infos[i] = {l, r, c};}int res = 0;sort(infos + 1, infos + q + 1);for(int i = 1; i <= q; i ++){auto [l, r, c] = infos[i];int j = find(l); res += c; while(j < r){int t = find(j + 1); merge(j, t);j = t; res += c;} }for(int i = 1; i <= n; i ++){if(find(i) != find(1)){res = -1;}}cout << res << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
Problem Two : 带权并查集维护到根节点最大距离
A-LCT_2024牛客暑期多校训练营4 (nowcoder.com)
Note the unusual memory limit for this problem.
Given a rooted tree with n \textstyle n n nodes and n − 1 \textstyle n-1 n−1 edges. The i \textstyle i i-th edge can be described by ( a i , b i ) \textstyle (a_i, b_i) (ai,bi), which represents an edge connecting node a i \textstyle a_i ai and node b i \textstyle b_i bi, where node a i \textstyle a_i ai is the parent of node b i \textstyle b_i bi.
There are n − 1 \textstyle n-1 n−1 queries. The i \textstyle i i-th query contains an integer c i \textstyle c_i ci, asking for the length of the longest simple path starting from node c i \textstyle c_i ci in the graph (forest) formed by the first i \textstyle i i edges. It is guaranteed that there does not exist j \textstyle j j such that 1 ≤ j ≤ i \textstyle 1 \leq j \leq i 1≤j≤i and b j = c i \textstyle b_j = c_i bj=ci, i.e., c i \textstyle c_i ci is the root of a tree in the forest.
给 n n n 个点,添加 n − 1 n-1 n−1 条边,每次询问某个树根代表的树的最大深度,并查集路径压缩维护每个点到根节点的距离以及每棵树的最大深度。
#include<bits/stdc++.h>
using namespace std;
#define int long longint const N = 1e6 + 10;int n, p[N], d[N], mx[N];int find(int x){if(x == p[x]) return x;int t = find(p[x]);d[x] += d[p[x]];return p[x] = t;
}void merge(int x, int y){int fx = find(x), fy = find(y);if(fx != fy){p[x] = fy;d[x] = d[y] + 1;mx[fy] = max(mx[fy], d[y] + mx[fx] + 1);}
}void solve(){cin >> n;for(int i = 1; i <= n; i ++){p[i] = i;d[i] = 0;mx[i] = 0;}for(int i = 1; i < n; i ++){int a, b, c;cin >> a >> b >> c;merge(b, a);cout << mx[find(c)] << ' ';}cout << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;cin >> T;while (T --){solve();}return 0;
}
Problem Three : 维护前缀和判定关系
4286. 多少个答案是错误的 - AcWing题库
有一个长度为 N 的整数序列。
下面会按顺序给出 M 个对该序列的描述,每个描述给定三个整数 l,r,s,表示该序列的第 l 个元素至第 r 个元素相加之和为 s。
对于每个描述,你需要判断该描述是否会与前面提到的描述发生冲突,如果发生冲突,则认为该描述是错误的。
如果一个描述是错误的,则在对后续描述进行判断时,应当将其忽略。
请你计算一共有多少个描述是错误的。
我们将每次查询区间元素之和转化为查询前缀和关系。
对于 l , r , s l,r,s l,r,s ,如果 l l l 与 r r r 的前缀和关系确定,那么 p r e f i x r − p r e f i x l − 1 prefix_r-prefix_{l-1} prefixr−prefixl−1 就应该等于 s s s 。
如果当前前缀和关系尚未确定,那么维护这次关系 l , r , s l,r,s l,r,s 。
注意要维护 n + 1 n+1 n+1 个点。
关于 : 为什么对于每个 l , r l,r l,r ,不直接维护 l , r l,r l,r 的关系,表示 r r r 到 l l l 的距离呢 ?
实际上确定区间 l , r l,r l,r 的关系,只需要知道 r r r 与 l − 1 l-1 l−1 是否存在关系即可,例如
1 5 1 3 4 5 1\;5 \\ 1\;3 \\ 4\; 5 151345
这种询问, 4 5 4\;5 45 只需要知道 5 5 5 跟 3 3 3 是否存在关系即可,因此我们每次维护 r r r 跟 l − 1 l-1 l−1 的关系即可。
#include<bits/stdc++.h>
using namespace std;
#define int long longint const N = 2e5 + 10;int n, m;
int p[N], d[N];int find(int x){if(x == p[x]) return x;int t = find(p[x]);d[x] += d[p[x]];return p[x] = t;
}void solve(){cin >> n >> m;for(int i = 0; i <= n; i ++){p[i] = i;d[i] = 0;}int res = 0;while(m --){int l, r, s;cin >> l >> r >> s;l --;if(find(l) == find(r)){res += (s != d[r] - d[l]);}else{int pl = find(l), pr = find(r);if(pl < pr){p[pr] = pl;d[pr] = -d[r] + s + d[l]; }else{p[pl] = pr;d[pl] = d[r] - s - d[l];}}}cout << res << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
Problem Four : 维护前缀和判定关系
239. 奇偶游戏 - AcWing题库
跟上一题的本质相同,还是维护前缀和之间的关系,不过我们这次的距离对 2 2 2 取模,仅维护到根节点的奇偶性即可, 0 0 0 表示偶数。 1 1 1 表示奇数。尚未确定的查询维护出来,否则检查给出的奇偶性是否符合已有的奇偶性。
#include<bits/stdc++.h>
using namespace std;
#define int long longint n, m;struct Query{int l, r, tp;
}q[5100];unordered_map<int, int> p, d;
int find(int x, unordered_map<int, int> &mp){if(x == mp[x]) return x;int t = find(mp[x], mp);(d[x] += d[mp[x]]) %= 2;return mp[x] = t;
}void solve(){cin >> n >> m;for(int i = 1; i <= m; i ++){int l, r;string s;cin >> l >> r >> s;l --;q[i] = {l, r, s == "odd" ? 1 : 0};p[l] = l, p[r] = r;d[l] = d[r] = 0;} for(int i = 1; i <= m; i ++){auto& [l, r, tp] = q[i];int pl = find(l, p), pr = find(r, p);if(pl == pr){if(((d[r] - d[l]) % 2 + 2) % 2 != tp){cout << i - 1 << '\n';return ;}}else{p[pr] = pl;d[pr] = ((d[l] + tp - d[r]) % 2 + 2) % 2;}}cout << m << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
Problem Five : 判定关系
4288. 研究虫子 - AcWing题库
这题比较简单,之所以拿出来,是加深并查集检查关系正确与否的思想。
关系尚不确定的,并查集维护关系。关系可以确定的,根据题目要求进行检查。
#include<bits/stdc++.h>
using namespace std;
#define int long longint n, m;
int p[2100], d[2100];int find(int x){if(x == p[x]) return x;int t = find(p[x]);(d[x] += d[p[x]]) %= 2;return p[x] = t;
}void solve(int yyy){cin >> n >> m;for(int i = 1; i <= n; i ++){p[i] = i;d[i] = 0;}bool fg = false;while(m --){int a, b;cin >> a >> b;int pa = find(a), pb = find(b);if(pa != pb){p[pb] = pa;d[pb] = ((1 + d[a] - d[b]) % 2 + 2) % 2;}else{if(((d[a] - d[b]) % 2 + 2) % 2 != 1){fg = true;}}}cout << "Scenario #"<<yyy<<":\n";cout << (fg ? "Suspicious bugs found!" : "No suspicious bugs found!") << '\n';cout << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;cin >> T;for(int i = 1; i <= T; i ++){solve(i);}return 0;
}
Problem Six : 判定树 - 无向图
4290. 小希的迷宫 - AcWing题库
给你 m m m 条无向边,构成无向图,判定图是不是树的形式
满足以下两个性质即可 :
-
连通性 : 树根只有一个
-
无环性 : 并查集判定是否有回路
(注意还要定义空图是不是树)
#include<bits/stdc++.h>
using namespace std;
#define int long long
int const N = 1e5 + 10;
int a, b, p[N];int find(int x){if(x == p[x]) return x;return p[x] = find(p[x]);
}// t 数组用于维护 p 数组初始化
// 输入 n 次之后一定不是树,所以开 N << 1
int cnt = 0, t[N << 1]; void solve(){bool fg = true;for(int i = 1; i <= 100000; i ++){p[i] = i;}while(cin >> a >> b){if(a == -1 && b == -1){return ;}if(a == 0 && b == 0){ for(int i = 1; fg && i < cnt; i ++){if(find(t[i]) != find(t[i + 1])){fg = false;}}cout << (fg ? "Yes" : "No") << '\n';for(int i = 1; i <= cnt; i ++){p[t[i]] = t[i];}cnt = 0;fg = true;continue ;}if(fg == false) continue ; // 不再维护, 已经不合法t[++ cnt] = a, t[++ cnt] = b;if(find(a) == find(b)) fg = false;else p[find(b)] = find(a);}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
Problem Seven : 判定树 - 有向图
3409. 这是一棵树吗 - AcWing题库
给你 m m m 条有向边,判定是否是树
需要满足以下性质 :
-
除了根节点以外,所有点入度均为 1 1 1
-
整个图连通 或者 没有环
只满足性质 1 1 1 ,可能是外向基环树 + 有根树构成的森林,所以还要判定连通性,保证只有一颗树,就没有外向基环树了。
或者直接当成无向边判环,把外向基环树判掉。
判环 Code :
#include<bits/stdc++.h>
using namespace std;
#define int long long
int in[10010], p[10010];
int find(int x){if(x == p[x]) return x;return p[x] = find(p[x]);
}
void solve(){int a, b, cnt = 1;fill(in + 1, in + 10001, -1);for(int i = 1; i <= 10000; i ++){p[i] = i;}while(cin >> a >> b){if(a == -1 && b == -1) return ;if(a == 0 && b == 0){int s0 = 0, s1 = 0, s2 = 0;for(int i = 1; i <= 10000; i ++){p[i] = i;if(in[i] == -1) continue ;if(in[i] == 0) s0 ++;else if(in[i] == 1) s1 ++;else s2 ++;}
// cout << s0 << ' ' << s1 << ' ' << s2 << '\n';if((s2 || s0 != 1) && ((!s0 && !s1 && !s2) == false)){cout << "Case " << cnt << " is not a tree.\n";}else{cout << "Case " << cnt << " is a tree.\n";}fill(in + 1, in + 10001, -1);
// for(int i = 1; i <= 10000; i ++) in[i] = 0;cnt ++;continue ;}int pa = find(a), pb = find(b);if(pa == pb) in[b] = 2;else p[pb] = pa;if(in[b] == -1) in[b] = 0;if(in[a] == -1) in[a] = 0;if(a == b) in[b] = 2; // 自环的处理in[b] ++;}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
// 只有一个 in[] = 0, else = 1
判联通性 Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
int in[10010], p[10010];
int find(int x){if(x == p[x]) return x;return p[x] = find(p[x]);
}
void solve(){int a, b, cnt = 1;fill(in + 1, in + 10001, -1);for(int i = 1; i <= 10000; i ++){p[i] = i;}while(cin >> a >> b){if(a == -1 && b == -1) return ;if(a == 0 && b == 0){int s0 = 0, s1 = 0, s2 = 0;int fsP = -1;for(int i = 1; i <= 10000; i ++){if(in[i] == -1) continue ;fsP = (fsP == -1 ? i : fsP);if(in[i] == 0) s0 ++;else if(in[i] == 1) s1 ++;else s2 ++;}for(int i = 1; i <= 10000; i ++){if(in[i] == -1) continue ;if(find(i) != find(fsP)){s2 = 1000;}}
// cout << s0 << ' ' << s1 << ' ' << s2 << '\n';if((s2 || s0 != 1) && ((!s0 && !s1 && !s2) == false)){cout << "Case " << cnt << " is not a tree.\n";}else{cout << "Case " << cnt << " is a tree.\n";}for(int i = 1; i <= 10000; i ++){p[i] = i;}fill(in + 1, in + 10001, -1);
// for(int i = 1; i <= 10000; i ++) in[i] = 0;cnt ++;continue ;}int pa = find(a), pb = find(b);if(pa == pb) {}//in[b] = 2;else p[pb] = pa;if(in[b] == -1) in[b] = 0;if(in[a] == -1) in[a] = 0;if(a == b) in[b] = 2; // 自环的处理in[b] ++;}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
// 只有一个 in[] = 0, else = 1
Problem Eight : 带权并查集维护距离
4287. 导航噩梦 - AcWing题库
4 4 4 个方向有 4 4 4 个距离,带权并查集维护两种距离, d x dx dx 维护横轴距离, d y dy dy 维护纵轴距离,对于每个查询,对应的曼哈顿距离 ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ |x_1-x_2|+|y_1-y_2| ∣x1−x2∣+∣y1−y2∣ 的 x x x 之差与 y y y 之差是相互独立的,我们分别进行查询即可。
#include<bits/stdc++.h>
using namespace std;
#define int long longint const N = 40010;
int const M = 40010;int n, m, k;
struct info{int a, b, l;char d;vector<pair< pair<int, int>, int> > ask;
}infos[M];int ans[N];int p[N], dx[N], dy[N];int find(int x){if(x == p[x]) return x;int t = find(p[x]);dx[x] += dx[p[x]];dy[x] += dy[p[x]];return p[x] = t;
}void solve(){cin >> n >> m;for(int i = 1; i <= n; i ++){p[i] = i;dx[i] = 0;dy[i] = 0;}for(int i = 1; i <= m; i ++){int a, b, c;char x;cin >> a >> b >> c >> x;infos[i] = {a, b, c, x};}cin >> k;for(int i = 1; i <= k; i ++){int a, b, I;cin >> a >> b >> I;infos[I].ask.push_back({ {a, b}, i});}for(int i = 1; i <= m; i ++){auto &[a, b, d, x, vc] = infos[i];{int pa = find(a), pb = find(b);if(pa != pb){p[pb] = pa;dx[pb] = dx[a] + (x == 'E' ? d : (x == 'W' ? -d : 0)) - dx[b];dy[pb] = dy[a] + (x == 'N' ? d : (x == 'S' ? -d : 0)) - dy[b];}}if(vc.size()){for(auto& [pr, id] : vc){auto& [a, b] = pr;int pa = find(a), pb = find(b);ans[id] = (pa == pb ? abs(dx[b] - dx[a]) + abs(dy[b] - dy[a]) : -1); }}}for(int i = 1; i <= k; i ++) cout << ans[i] << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); solve();return 0;
}
Problem Nine : 并查集维护连通分量信息
可以用并查集维护集合 m a x max max ,集合 m i n min min 等等集合信息。
本题是维护集合 m a x max max 的编号,如果有多个 m a x max max ,取最小编号。
注意这种维护只有祖先节点的值有意义,所以我们在 find 祖先节点的过程中不需要维护 m a x max max 信息,因为他们已经位于同一个连通块。
进行合并的时候,指定一个祖先节点,将另一个祖先的 m a x max max 与之比较,维护 m a x max max 信息。
因为并查集删边很难,加边简单。所以先全删除要删除的边,然后维护并查集,倒着加边,根据需要输出信息即可。
#include<bits/stdc++.h>
using namespace std;
#define int long longint const N = 10010;
int const M = 20010;
int const Q = 50010;struct Edge{int a, b;
}edges[M];
set<pair<int, int> > st;
int n, m, q;
int v[N];
struct Query{int tp;int a, b;
}querys[Q];int p[N], d[N];// 注意这种维护只有祖先结点的值有意义
// 所以已经位于同一个连通块的点不用维护
int find(int x){if(x == p[x]) return x;return p[x] = find(p[x]);
}
int cal(int a, int b){if(v[a] == v[b]) return min(a, b);else if(v[a] > v[b]) return a;return b;
}
void merge(int a, int b){int pa = find(a), pb = find(b);if(pa != pb){p[pb] = pa;d[pa] = cal(d[pa], d[pb]);}
}void solve(){for(int i = 1; i <= n; i ++){cin >> v[i];p[i] = i;d[i] = i;}st.clear();cin >> m;for(int i = 1; i <= m; i ++){int a, b;cin >> a >> b;if(a > b) swap(a, b);edges[i] = {++ a, ++ b};}cin >> q;for(int i = 1; i <= q; i ++){string op;int a, b;cin >> op;if(op == "query"){cin >> a; querys[i] = {0, ++ a};}else{cin >> a >> b;if(a > b) swap(a, b);querys[i] = {1, ++ a, ++ b};st.insert({a, b});}}for(int i = 1; i <= m; i ++){auto& [a, b] = edges[i];if(st.count({a, b}) == false){// cout << "merge: " << a << ' ' << b << '\n'; merge(a, b);}}std::vector<int> ans;for(int i = q; i >= 1; i --){int tp = querys[i].tp;if(tp == 0){int a = querys[i].a, pa = find(a);if(v[d[pa]] > v[a]){ans.push_back(d[pa] - 1);}else{ans.push_back(-1);}}else{int a = querys[i].a, b = querys[i].b;// cout << "Merge: " << i << ' ' << a << ' ' << b << '\n';// cout << d[find(a)] << '\n';merge(a, b);}}for(auto i = ans.rbegin(); i != ans.rend(); i ++){cout << (*i) << '\n';}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); int fg = 0;while(cin >> n){if(!fg) fg = 1;else cout << '\n';solve(); }return 0;
}
下面是对拍时用到的代码 :
int cnt = 0;
pair<int, int> edge[1000];
set<pair<int, int> > st;int main(){// 生成随机数种子,利用 timeb 生成毫秒级别随机数struct _timeb T;_ftime(&T);srand(T.millitm); int n = Data(2, 5);cout << n << '\n';for(int i = 1; i <= n; i ++){cout << Data(1, 10) << " \n"[i == n];}int m = Data(1, n * (n - 1) / 2);cout << m << '\n';for(int i = 1; i <= m; i ++){int a, b;while(true){a = Data(1, n);b = Data(1, n); if(a > b) swap(a, b);if(a == b) continue ;if(st.count({a, b}) == false) break;}-- a, -- b;st.insert({a, b});edge[++ cnt] = {a, b};cout << a << ' ' << b << '\n';}int q = Data(1, 5);cout << q << '\n';for(int i = 1; i <= q; i ++){int op = Data(1, 2);if(cnt == 0 && op == 1) op = 0;if(op == 1){cout << "destroy ";int e = Data(1, cnt);cout << edge[e].first << ' ' << edge[e].second << '\n';swap(edge[e], edge[cnt]);cnt --;}else{cout << "query ";int a = Data(1, n);-- a;cout << a << '\n';}}return 0;
}
Problem Ten : 并查集判定关系
258. 石头剪子布 - AcWing题库
这题题面有问题,我修改成了下面这个,并且提交了工单。
输出格式
每组测试用例输出一行结果。
如果只能有一个人是裁判,则输出他的编号和确定他是唯一裁判的轮数。
如果裁判的人选多于 1 个,则输出
Can not determine。如果必须存在多名裁判或者必须没有裁判,则输出
Impossible。具体格式可参考样例。
做法如下 :
枚举每个人是否可能是裁判,如果当前枚举的人不可能是裁判,记录确定他一定不是裁判时的编号。
最后查看裁判人选, ≥ 2 \geq 2 ≥2 时无法判定谁是裁判。
= 1 =1 =1 说明只有一个人可能是裁判,假设这个人编号为 j j j, 只要确定其他人全部不是就可以了,假设第 i i i 个人第 t i t_i ti 轮被确定不是裁判, r e s = max i ≠ j t i res=\max_{i\neq j} t_i res=maxi=jti
= 0 =0 =0 说明只有一个裁判的情况,所有关系都不合法,也就是说必须有多个裁判。
至于必须没有裁判的情况,这是不可能的,如果没有裁判不发生冲突,此时我们任意指定一个人为裁判都合法,所以不可能必须没有裁判。
#include<bits/stdc++.h>
using namespace std;
#define int long longint n, m;struct Info{int a, b, dis;
}infos[2100];int p[510], d[510];int find(int x){if(x == p[x]) return x;int t = find(p[x]);d[x] = (d[x] + d[p[x]]) % 3;return p[x] = t;
}void merge(int a, int b, int dis){int pa = find(a), pb = find(b);p[pb] = pa;d[pb] = ((dis + d[a] - d[b]) % 3 + 3) % 3;
} void solve(){for(int i = 1; i <= m; i ++){string s;int pos;cin >> s;for(int j = 0; j < s.size(); j ++){if(isdigit(s[j]) == false){pos = j;break;}}int a = stoi(s.substr(0, pos));int b = stoi(s.substr(pos + 1));int dis = (s[pos] == '=' ? 0 : (s[pos] == '<' ? 2 : 1));++ a, ++ b;infos[i] = {a, b, dis};} vector<int> v, pos;for(int judge = 1; judge <= n; judge ++){for(int i = 1; i <= n; i ++){p[i] = i;d[i] = 0;}bool fg = true;for(int i = 1; i <= m; i ++){auto& [a, b, dis] = infos[i];if(a == judge || b == judge) continue ;int pa = find(a), pb = find(b);if(pa != pb){merge(a, b, dis);}else{if(((d[b] - d[a]) % 3 + 3) % 3 != dis){pos.push_back(i);fg = false;break;} }}if(fg){v.push_back(judge);}} if(v.size() >= 2){puts("Can not determine"); }else if(v.size() == 1){int res = ((size_t)pos.size() ? *max_element(pos.begin(), pos.end()) : 0);printf("Player %lld can be determined to be the judge after %lld lines\n", v[0] - 1, res);}else{puts("Impossible"); }
}signed main(){// ios::sync_with_stdio(false);// cin.tie(0), cout.tie(0); while(cin >> n >> m){solve(); }return 0;
}
需要对拍数据可以用下面的,加上 0 0 表示结尾
#include<bits/stdc++.h>
using namespace std;// 0 <= rand()%(a+1) <= a
// k <= rand()%(a+1) <= a+k
// windows : rand() 生成的随机数在 0~32767 之间
/*生成一个 1 <= a <= 1,000,000 long long Random(long long mod){long long ans = 2147483647;return ans * rand() % mod + 1;}取 mod = 1, 000, 000
*/ // [k, k+mod-1]
long long Random(long long k, long long mod){long long ans = 2147483647;return ans * rand() % mod + k;
}long long Data(long long l, long long r){return Random(l, r - l + 1);
}int main(){// 生成随机数种子,利用 timeb 生成毫秒级别随机数struct _timeb T;_ftime(&T);srand(T.millitm); int n, m;n = Data(2, 5);m = Data(1, 10);cout << n << ' ' << m << '\n';for(int i = 1; i <= m; i ++){int op = Data(1, 3);int a = Data(1, n), b = Data(1, n);while(a == b){a = Data(1, n);b = Data(1, n);}if(a > b) swap(a, b);-- a, -- b;char x;if(op == 1){x = '=';}else if(op == 2){x = '<';}else{x = '>';}string res = to_string(a) + x + to_string(b);cout << res << '\n';}cout <<"0 0";return 0;
}
Problem Eleven : 并查集维护位置信息
145. 超市 - AcWing题库
超市里有 N 件商品,每件商品都有利润 pi 和过期时间 di,每天只能卖一件商品,过期商品不能再卖。
求合理安排每天卖的商品的情况下,可以得到的最大收益是多少。
没想出来,感觉要贪心,看看题解吧。
做法一 :
我们倒着枚举天数,对于每种天数,把当前能卖的放进来,因为是倒着枚举,那么以后这些商品都可以卖,我们当然优先卖最大的,大根堆维护一下。
每组测试用例 : O ( n log n ) O(n \log n) O(nlogn)
int n;
vector<int> goods[N];void solve(){for(int i = 1; i <= 10000; i ++){goods[i].clear();}for(int i = 1; i <= n; i ++){int p, d;cin >> p >> d;goods[d].push_back(p);}int ans = 0;priority_queue<int> q;for(int i = 10000; i >= 1; i --){for(auto &p : goods[i]){q.push(p);}if(q.size()){ans += q.top();q.pop();}}cout << ans << '\n';
}
做法二 :
做法一的本质,实际上就是对于每个利润大的商品,把它安排尽量晚的卖出。那么我们并查集维护能卖的位置即可,对于 p p p 如果使用了,就把他跟 p − 1 p-1 p−1 合并。
O ( n + α ( n ) ) O(n+\alpha(n)) O(n+α(n))
#include<bits/stdc++.h>
using namespace std;
#define int long longint n;
int const N = 1e4 + 10;
int p[N]; // 维护每个位置的能用的最左边位置struct node{int p, d;bool operator < (const node & T) const {return p > T.p;}
}goods[N];int find(int x){if(x == p[x]) return x;return p[x] = find(p[x]);
}void merge(int a, int b){int pa = find(a), pb = find(b);if(pa != pb){if(pa < pb) p[pb] = pa;else p[pa] = pb;}
}void solve(){for(int i = 0; i <= 10000; i ++){p[i] = i;}for(int i = 1; i <= n; i ++){int p, d;cin >> p >> d;goods[i] = {p, d};}sort(goods + 1, goods + n + 1);int ans = 0;for(int i = 1; i <= n; i ++){auto &[p, d] = goods[i];int pos = find(d);if(pos){ans += p;merge(pos, pos - 1);}}cout << ans << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); while(cin >> n){solve();}return 0;
}
Problem Twelve : 并查集维护关系
kuangbin 专题里我留到最后一题,耗时最久的一题。
实际不是很难,但自己的 DP 出了点小问题,找了好久,对拍一开始没写对,又浪费了很长时间。
如果 a a a 说 b b b 是天使,
假设 a a a 是天使,那么 b b b 也是天使 ;假设 a a a 是魔鬼,那么 b b b 也是魔鬼
如果 a a a 说 b b b 是魔鬼,
假设 a a a 是魔鬼,那么 b b b 是天使 ;假设 a a a 是天使,那么 b b b 是魔鬼。
所以不难看出,回答 y e s yes yes 是 a a a 与 b b b 是同类 ,回答 n o no no 时 a a a 与 b b b 是异类。
所以我们用并查集维护。
维护之后,会得到很多互不连通的并查集,每个并查集与根节点距离为 0 0 0 的设有 x x x 个,距离为 1 1 1 设有 y y y 个, D P DP DP 求一下选出 p 1 p1 p1 个人的方案数,如果为 1 1 1 ,回溯输出天使编号 ;否则输出魔鬼编号。
#include<bits/stdc++.h>
using namespace std;
#define int long longint n, m, p1, p2;struct info{int x, y, dis;
}infos[1100];int p[610], d[610]; int find(int x){if(x == p[x]) return x;int t = find(p[x]);d[x] = (d[x] + d[p[x]]) % 2;return p[x] = t;
}pair<int, int> bk[610]; // 每个连通块的 0 1 数量
vector<int> same[610];
vector<int> dif[610];
map<int, int> mp;
int cnt = 0;
void debug_print(vector<vector<int> > &f) {cout << "Union-Find state:\n";for (int i = 1; i <= n; i++) {cout << "Node " << i << ": parent = " << p[i] << ", distance = " << d[i] << '\n';}cout << "BK array:\n";for (int i = 1; i <= cnt; i++) {cout << "Block " << i << ": 0's = " << bk[i].first << ", 1's = " << bk[i].second << '\n';}cout << "DP table:\n";for (int i = 0; i <= cnt; i++) {for (int j = 0; j <= p1; j++) {cout << f[i][j] << ' ';}cout << '\n';}
}void solve(){n = p1 + p2;cnt = 0;mp.clear();for(int i = 1; i <= n; i ++){p[i] = i;d[i] = 0;bk[i] = {0, 0};same[i].clear();dif[i].clear();}for(int i = 1; i <= m; i ++){int x, y;string s;cin >> x >> y >> s;infos[i] = {x, y, s == "no"};// cout << x << ' ' << y << ' ' << (s == "no") << '\n';}for(int i = 1; i <= m; i ++){auto &[x, y, tp] = infos[i];if(x == y) continue ;int px = find(x), py = find(y);if(px != py){p[py] = px;d[py] = ((d[x] + tp - d[y]) % 2 + 2) % 2;}else{int t = ((d[x] - d[y]) % 2 + 2) % 2;if(t != tp){cout << "break\n";return ;}}}// cout << find(1) << ' ' << find(2) << '\n';// cout << d[1] << ' ' << d[2] << '\n';for(int i = 1; i <= n; i ++){if(find(i) == i){mp[i] = ++ cnt;}}for(int i = 1; i <= n; i ++){int pi = find(i), id = mp[pi];if(d[i] == 0){bk[id].first ++;same[id].push_back(i);}else{bk[id].second ++;dif[id].push_back(i);}}// f[i][j] 表示考虑到第 i 个连通块, 划分出来 p1 个天使的方案数vector<vector<int> > f(cnt + 1, vector<int> (p1 + 1, 0));f[0][0] = 1;if(bk[1].first <= p1) f[1][bk[1].first] ++ ;if(bk[1].second <= p1) f[1][bk[1].second] ++ ;for(int i = 1; i < cnt; i ++){int fs = bk[i + 1].first, sc = bk[i + 1].second;for(int j = 0; j <= p1; j ++){if(f[i][j]){if(j + fs <= p1){f[i + 1][j + fs] += f[i][j];if(f[i + 1][j + fs] > 1e9) f[i + 1][j + fs] = 1e9;}if(j + sc <= p1){f[i + 1][j + sc] += f[i][j];if(f[i + 1][j + sc] > 1e9) f[i + 1][j + sc] = 1e9;}}}}// debug_print(f);// cout << "f[1][0] : " << f[1][0] << '\n';// cout << "f[1][1] : " << f[1][1] << '\n';// cout << "f[2][1] : " << f[2][1] << '\n';// for(int i = 1; i <= n; i ++){// cout << i << ' ' << find(i) << '\n';// }// cout << "cnt: ";// cout << cnt << '\n';// for(int i = 1; i <= cnt; i ++){// cout << bk[i].first << ' ' << bk[i].second << '\n';// }// cout << f[cnt][p1] << '\n';// if(p1 != p2 && f[cnt][p1] == 1){if(f[cnt][p1] == 1){vector<int> choose(cnt + 1);int now = p1;for(int i = cnt; i >= 1; i --){int fs = bk[i].first, sc = bk[i].second;if(now >= fs && f[i - 1][now - fs] == 1){now -= fs;// cout << fs << '\n';choose[i] = (fs);}else if(now >= sc && f[i - 1][now - sc] == 1){now -= sc;// cout << sc << '\n';choose[i] = (sc);}}vector<int> res;for(int i = 1; i <= cnt; i ++){int t = choose[i];// cout << "t: " << t << '\n';if(t == bk[i].first){for(int j = 0; j < same[i].size(); j ++){res.push_back(same[i][j]);}}else{for(int j = 0; j < dif[i].size(); j ++){res.push_back(dif[i][j]);}}}sort(res.begin(), res.end());for(auto &x : res) cout << x << '\n';cout << "end\n";}else{cout << "no\n";}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0); while(cin >> m >> p1 >> p2, m || p1 || p2){solve();}return 0;
}
// 要求唯一确定每个居民的身份
// f[i][j] 表示考虑到第 i 个并查集, 得到 j 个天使的方案数对拍数据 (不保证给定关系不发生冲突) :
#include<bits/stdc++.h>
using namespace std;// 0 <= rand()%(a+1) <= a
// k <= rand()%(a+1) <= a+k
// windows : rand() 生成的随机数在 0~32767 之间
/*生成一个 1 <= a <= 1,000,000 long long Random(long long mod){long long ans = 2147483647;return ans * rand() % mod + 1;}取 mod = 1, 000, 000
*/ // [k, k+mod-1]
long long Random(long long k, long long mod){long long ans = 2147483647;return ans * rand() % mod + k;
}long long Data(long long l, long long r){return Random(l, r - l + 1);
}int main(){// 生成随机数种子,利用 timeb 生成毫秒级别随机数struct _timeb T;_ftime(&T);srand(T.millitm); // set<pair<int, int> > est;// est.insert({1, 2});// cout <<est.count({1,2})<<'\n';// cout <<est.count({2,1})<<'\n';int t = Data(1, 2);while(t --){int n, m, p1, p2;set<pair<int, int> > st = set<pair<int, int> > ();p1 = Data(1, 3);p2 = Data(1, 3);n = p1 + p2;m = Data(1, n * (n - 1) / 2);cout << m << ' ' << p1 << ' ' << p2 << '\n';while(m --){int x, y;while(true){x = Data(1, p1 + p2);y = Data(1, p1 + p2);if(x > y) swap(x, y);if(st.count({x, y})) continue;else break;}st.insert({x, y});int c = Data(1, 2);if(x == y) c = 2;cout << x << ' ' << y << ' ';if(c == 1) cout << "no\n";else cout << "yes\n";}}cout <<"0 0 0";return 0;
} 相关文章:

Disjoint Set Union
Problem One : 维护区间连通块 F - Range Connect MST (atcoder.jp) 暴力模拟的话,就是基于 Kruskal 的思想,按 c c c 从小到大排序,对于每次询问,枚举检查 j ∈ [ l , r ] j\in [l,r] j∈[l,r] ,只要 j j j 与 …...

手写 Hibernate ORM 框架 05-基本效果测试
手写 Hibernate 系列 手写 Hibernate ORM 框架 00-hibernate 简介 手写 Hibernate ORM 框架 00-环境准备 手写 Hibernate ORM 框架 01-注解常量定义 手写 Hibernate ORM 框架 02-实体 Bean 定义,建表语句自动生成 手写 Hibernate ORM 框架 03-配置文件读取, 数…...

Unity材质球自动遍历所需贴图
Unity材质球自动遍历所需贴图 文章目录 Unity材质球自动遍历所需贴图一、原理二、用法1.代码:2.使用方法 一、原理 例如一个材质球名为:Decal_Text_Cranes_01_Mat , 然后从全局遍历出:Decal_Text_Cranes_01_Albedo赋值给材质球的…...

C++那些事之结构化绑定
C那些事之结构化绑定 在聊结构化绑定之前,有几个面试问题,看看你会不会? 如何使用结构化绑定访问自定义类的私有成员?如何使用结构化绑定修改自定义类的成员呢? 这几个题目估计没几个人能答上来,题目与答案…...

ECRS工时分析软件:工业工程精益生产的智慧引擎
在工业工程学的广阔领域中,程序分析一直扮演着至关重要的角色。其中,ECRS四大原则——取消、合并、重排、简化,作为程序分析的核心,旨在通过优化生产过程,实现成本的节省和精益生产的目标。如今,随着科技的…...

大语言模型的核心岗位及其要求
一、核心岗位 研究科学家(Research Scientist): 负责制定研究计划,探索新算法和模型架构。数据科学家(Data Scientist): 进行数据收集、分析和预处理。机器学习工程师(Machine Lear…...

【屏驱MCU】RT-Thread 文件系统接口解析
本文主要介绍【屏驱MCU】基于RT-Thread 系统的文件系统原理介绍与代码接口梳理 目录 0. 个人简介 && 授权须知1. 文件系统架构1.1 虚拟文件系统目录架构 2. menuconfig 分析3. 代码接口分析3.1 DFS框架挂载目录3.2 【FAL抽象层】分区表和设备表3.3 如何将【文件路径】挂…...

进程管理工具top ps
概述 top 和 ps 是 Linux 系统中两个非常重要的用于管理和监控进程的命令工具。以下是它们的主要功能和区别: 1. 动静 2. 整体 & 详细 top: 动态视图:top 提供了一个实时动态更新的视图,能够持续显示系统中当前正在运行的进程…...

2年社招冲击字节,一天三面斩获offer
在工作满两年的时间选择了求变,带着运气和实力以社招身份重新看今天的互联网环境,从结果看还是复合预期的。 整个面试的流程还挺快的。周中让招聘专员给投递了简历。问什么时候面试,申请了一个周日,直接安排三面。下周周中就开启…...

oppo,埃科光电25届秋招,快手25届技术人才专项计划等几千家企业岗位内推
oppo,埃科光电25届秋招,快手25届技术人才专项计划等几千家企业岗位内推 ①【OPPO】25届秋招开启! 内推简历优先筛选! 【岗位类别】AI/算法类,软件类,硬件类,工程技术类,品牌策划类&a…...
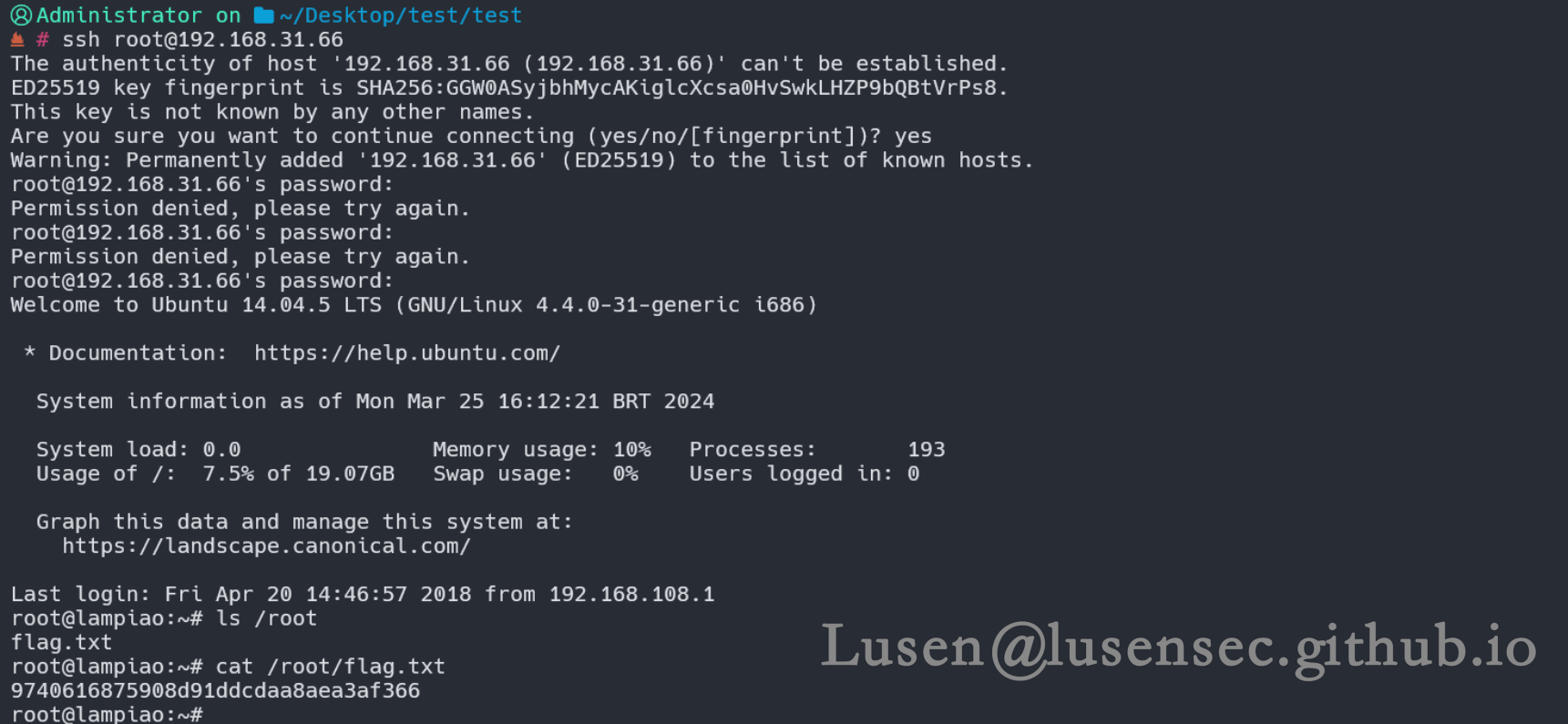
【Vulnhub系列】Vulnhub Lampiao-1 靶场渗透(原创)
【Vulnhub系列靶场】Vulnhub Lampiao-1靶场渗透 原文转载已经过授权 原文链接:Lusen的小窝 - 学无止尽,不进则退 (lusensec.github.io) 一、主机发现 二、端口扫描 三、web框架 四、web渗透 1、信息收集 2、目录扫描 获得版本信息7.56 3、获取shell …...

MySQL:ORDER BY 排序查询
通过 ORDER BY 条件查询语句可以查询到符合用户需求的数据,但是查询到的数据一般都是按照数据最初被添加到表中的顺序来显示。 基本语法 在MySQL中,排序查询主要通过ORDER BY子句实现。其基本语法如下: SELECT column1, column2, ... FR…...

UML类图 详解
总目录 前言 作为一个程序员,我们经常会使用UML来绘制各种图(UML中定义了用例图、类图、时序图、协作图等九种),类图就是其中常用图之一。设计模式中经常会用到的是类图,本文主要是学习UML类图相关资料后的汇总笔记&a…...

【IEEE出版 | 高录用率 | 快速检索 | 有ISBN号!】2024年智能计算与数据挖掘国际学术会议 (ICDM 2024,9月20-22)
智能计算与数据挖掘是当今信息技术领域的研究热点,并在众多领域都有着广泛的应用,如金融、医疗、教育、交通等。随着大数据时代数据量爆炸式增长,如何从海量数据中提取有价值的信息,一直是需要迭代解决的问题。 2024年智能计算与…...

DaoCloud配置不同环境的流水线(Q)
在DaoCloud自动化部署时,不知道如何分别构建生产,测试环境镜像。 Dockfile文件里有 ARG BUILD_ENV"uat" RUN npm run build:${BUILD_ENV} 这样两行代码来区分环境打包的,ARG是用于指定传递给构建运行时的变量,可是…...

基础的Shell命令
Shell命令有很多,以下是一些常用的Shell命令及其简要说明: 1. cd: 切换当前工作目录。 2. ls: 列出目录内容。 3. pwd: 显示当前工作目录的路径。 4. mkdir: 创建新目录。 5. rm: 删除文件或目录。 6. cp: 复制文件或目录。 7. mv: 移动文件或目录…...

量子仿真speedUp的经验
不用CPU的话,好的电脑配置对于jax的编译会更快 GPU编译速度明显最快...

电测量数据交换DLMS∕COSEM组件第61部分:对象标识系统(OBIS)(下)
GB/T 17215.6的本部分规定了对象标识系统(OBIS)的总体结构并将测量设备中的所有常用数据项映射到其标识代码。OBIS为测量设备中的所有数据都提供唯一的标识符,不仅包括测量值,而且还包括仪表设备的配置或获取测量设备运行状态的抽象数据。 5.抽象对象(A=0) 5.1通用和服…...

【Java】重生之String类再爱我一次---练习题(012)
目录 ♦️练习一:用户登录 ♦️练习二:遍历字符串 ♦️练习三:统计字符次数数 ♦️练习四:拼接字符串 ♦️练习五:反转字符串 ♦️练习六:金额转换 ♦️练习七:手机号屏蔽 ♦️练习一&am…...

NSSCTF-GDOUCTF 2023新生赛
[GDOUCTF 2023]hate eat snake 考察:js代码审计 打开题目,发现需要坚持60秒,那么简单的一个思路就是修改得分的变量>60即可 办法1:修改变量 右键查看源代码,之后发现有一个snake.js的文件,ctrlf搜索i…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
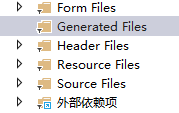
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...

Linux信号保存与处理机制详解
Linux信号的保存与处理涉及多个关键机制,以下是详细的总结: 1. 信号的保存 进程描述符(task_struct):每个进程的PCB中包含信号相关信息。 pending信号集:记录已到达但未处理的信号(未决信号&a…...
