dp:221. 最大正方形
221. 最大正方形

看到这个题目真能立马想到dp吗?貌似很难,即使知道是一个dp题也很难想到解法。
直观来看,使用bfs以一个点为中点进行遍历,需要的时间复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2)
但是可以很容易发现,如果求以一个点为角 构成的最大正方形,可以通过其他周围的点作为角来快速找到这个点的最大正方形。
我们用数组存以该点为右下角,左下角,左上角,右上角的最大正方形,可以通过周围的转移,然后求出以它为“中心”构成的最大正方形。于是有如下代码
class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int n = matrix.size();int m = matrix[0].size();if(n == 1 && m == 1) return matrix[0][0];vector<vector<vector<int>>> dp(n, vector<int>(m, vector<int>(4, 0)));int ans = 0;for(int j = 0; j < m; ++ j){dp[0][j][0] = dp[0][j][1]= dp[0][j][2] = dp[0][j][3] = matrix[0][j];}for(int i = 1; i < n - 1; ++ i){dp[i][0][0] = dp[i][0][1] = dp[i][0][2] = dp[i][0][3] = matrix[i][0];for(int j = 1; j < m - 1; ++ j){dp[i][j][0] = min(dp[i - 1][j][0], min(dp[i - 1][j - 1][0], dp[i][j - 1][0])) + 1;dp[i][j][1] = min(dp[i - 1][j][1], min(dp[i - 1][j + 1][1], dp[i][j + 1][1])) + 1;····}//最后一列}//最后一行return ans * ans;}
};
但是实际上,以该点为右下角就足以解决这个问题,因为对于任何一个最大正方形而言,它一定有一个右下角,那么找到这个右下角能构成的最大正方形就是这个正方形了。
class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int n = matrix.size();int m = matrix[0].size();if(n == 1 && m == 1) return matrix[0][0] - '0';vector<vector<int>> dp(n, vector<int>(m, 0));int ans = 0;for(int i = 0; i < m; ++ i){dp[0][i] = matrix[0][i] - '0';ans = max(ans, dp[0][i]);}for(int i = 1; i < n; ++ i){dp[i][0] = matrix[i][0] - '0';ans = max(ans, dp[i][0]);for(int j = 1; j < m; ++ j){if(matrix[i][j] == '0') dp[i][j] = 0;else dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;ans = max(ans, dp[i][j]);}}return ans * ans;}
};
相关文章:

dp:221. 最大正方形
221. 最大正方形 看到这个题目真能立马想到dp吗?貌似很难,即使知道是一个dp题也很难想到解法。 直观来看,使用bfs以一个点为中点进行遍历,需要的时间复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2) 但是可以很容易发现,…...

花10分钟写个漂亮的后端API接口模板!
你好,我是田哥 在这微服务架构盛行的黄金时段,加上越来越多的前后端分离,导致后端API接口规范变得越来越重要了。 比如:统一返回参数形式、统一返回码、统一异常处理、集成swagger等。 目的主要是规范后端项目代码,以及…...
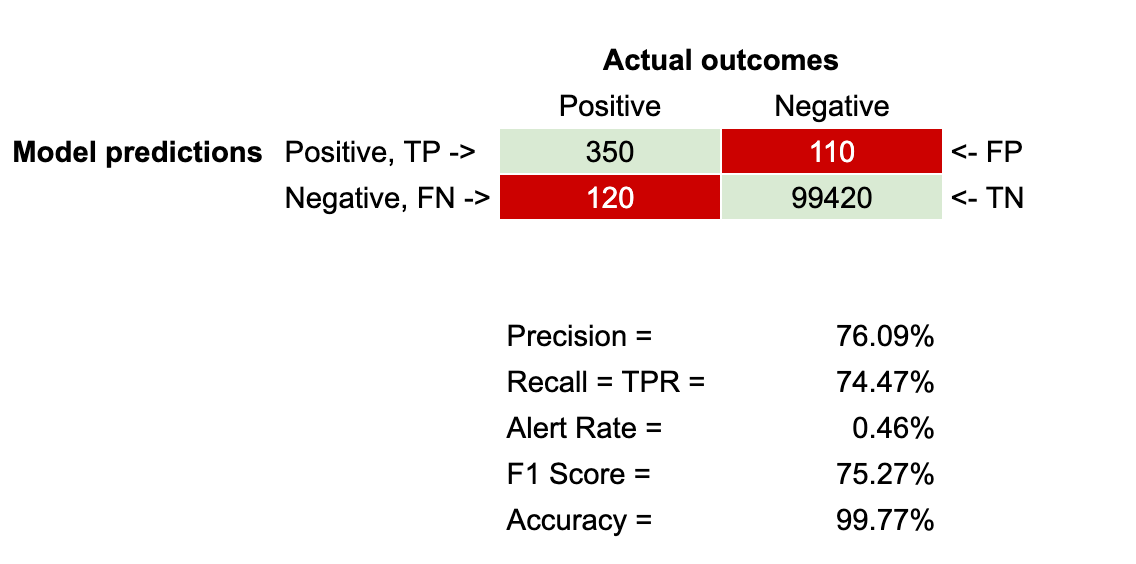
评估分类机器学习模型的指标
欢迎来到雲闪世界。一旦我们训练了一个监督机器学习模型来解决分类问题,如果这就是我们工作的结束,我们会很高兴,我们可以直接向他们输入新数据。我们希望它能正确地对所有内容进行分类。然而,实际上,模型做出的预测并…...

农机自动化:现代农业的未来趋势
随着人口的增长和农业生产的需求不断增加,提高农业生产效率成为现代农业的重要目标。农机自动化作为一种新兴技术,可以大幅度提升农机的使用效率和生产能力。农机自动化是指利用先进的传感技术、数据处理和人工智能技术,使农机能够自动完成农…...

25考研操作系统复习·1.1/1.2/1.3 操作系统的基本概念/发展历程/运行环境
目录 操作系统的基本概念 概念(定义) 功能和目标 资源的管理者 向上层提供服务 给普通用户的 给软件/程序员的 对硬件机器的拓展 操作系统的特征 操作系统的发展历程 操作系统的运行环境 操作系统的运行机制 中断和异常 中断的作用 中断的…...

如何培养学生的创新意识和实践能力
培养学生的创新意识和实践能力是一个复杂而系统的过程,涉及多个方面的努力和措施。以下是一些具体的做法: 一、培养学生的创新意识 提供创新环境: 为学生创造一个开放、自由、支持创新的学习环境,让他们能够自由地表达自己的想法…...
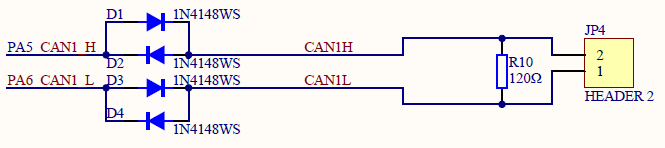
四、GD32 MCU 常见外设介绍(15)CAN 模块介绍
CAN是控制器局域网络(Controller Area Network)的简称,它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的,并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 CAN总线协议已经成为汽车计算机控…...

AIGC大模型产品经理高频面试大揭秘‼️
近期有十几个学生在面试大模型产品经理(薪资还可以,详情见下图),根据他们面试(包括1-4面)中出现高频大于3次的问题汇总如下,一共32道题目(有答案)。 29.讲讲T5和Bart的区…...

【嵌入式笔记】【C语言】struct union
结构体(Struct)定义: struct 结构体名 {member1; // 成员1,可以是任何基本数据类型或复合类型member2; // 成员2... };//例如: struct Point {float x;float y;...
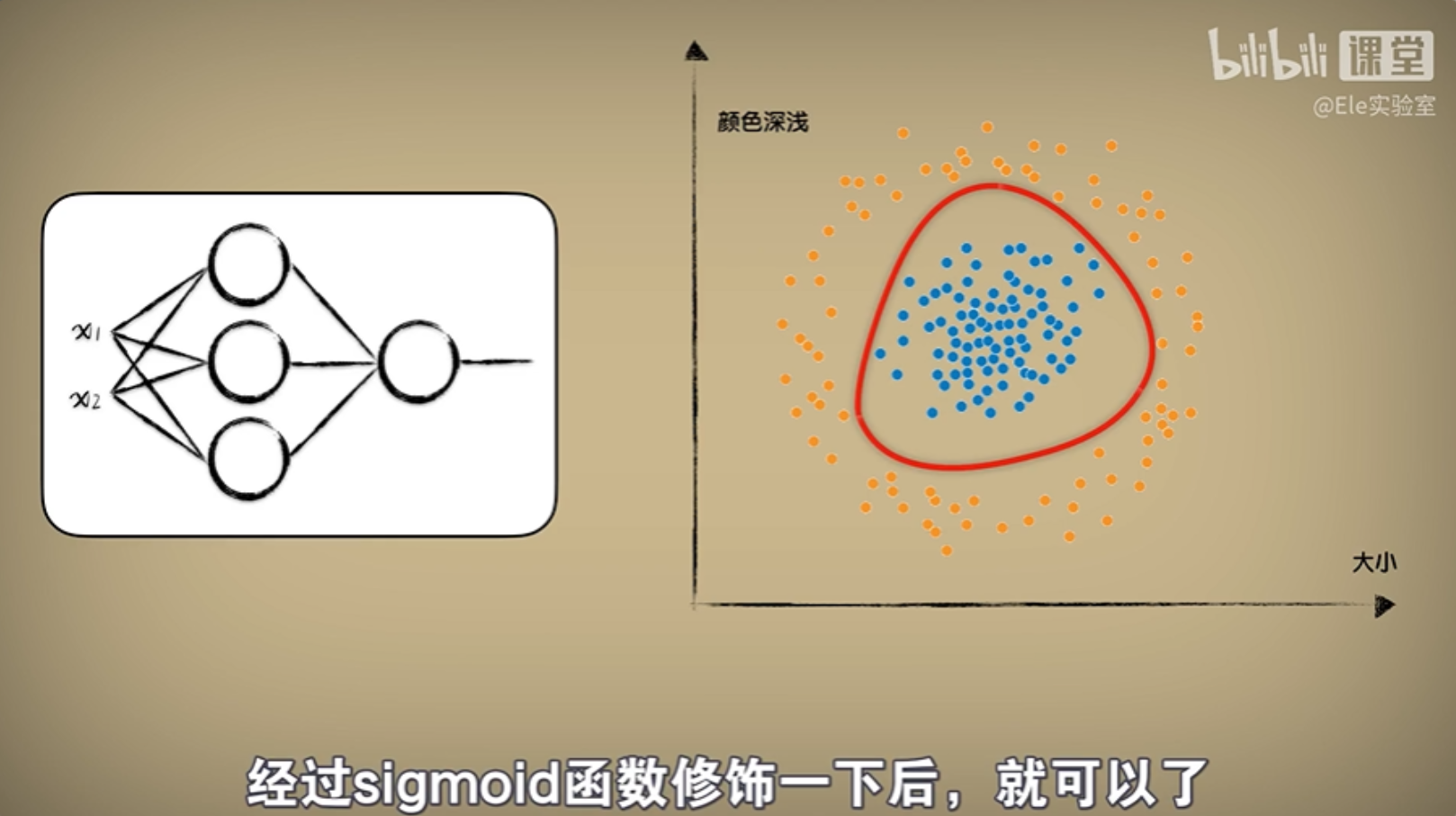
【初学人工智能原理】【9】深度学习:神奇的DeepLearning
前言 本文教程均来自b站【小白也能听懂的人工智能原理】,感兴趣的可自行到b站观看。 代码及工具箱 本专栏的代码和工具函数已经上传到GitHub:1571859588/xiaobai_AI: 零基础入门人工智能 (github.com),可以找到对应课程的代码 正文 深度…...

[RoarCTF 2019]Easy Calc1
打开题目 查看源码,看到 看到源代码有 calc.php,构造url打开 看到php审计代码, 由于页面中无法上传num,则输入 num,在num前加入一个空格可以让num变得可以上传,而且在进行代码解析时,php会把前…...
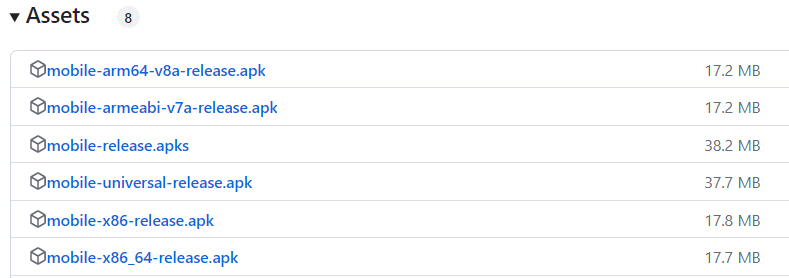
安卓APK安装包arm64-v8a、armeabi-v7a、x86、x86_64有何区别?如何选择?
在GitHub网站下载Android 安装包,Actions资源下的APK文件通常有以下版本供选择: 例如上图是某Android客户端的安装包文件,有以下几个版本可以选择: mobile-release.apk(通用版本,体积最大)mobi…...

【AI大模型】通义千问:开启语言模型新篇章与Function Call技术的应用探索
文章目录 前言一、大语言模型1.大模型介绍2.大模型的发展历程3.大模型的分类a.按内容分类b.按应用分类 二、通义千问1.通义千问模型介绍a.通义千问模型介绍b.应用场景c.模型概览 2.对话a.对话的两种方式通义千问API的使用 b.单轮对话Vue页面代码:Django接口代码 c.多…...

详细教程 MySQL 数据库 下载 安装 连接 环境配置 全面
数据库就是储存和管理数据的仓库,对数据进行增删改查操作,其本质是一个软件。 首先数据有两种,一种是关系型数据库,另一种是非关系型数据库。 关系型数据库是以表的形式来存储数据,表和表之间可以有很多复杂的关系&a…...

门控循环单元GRU
目录 一、GRU提出的背景:1.RNN存在的问题:2.GRU的思想: 二、更新门和重置门:三、GRU网络架构:1.更新门和重置门如何发挥作用:1.1候选隐藏状态H~t:1.2隐藏状态Ht: 2.GRU: 四、底层源码…...

程序员修炼之路
成为一名优秀的程序员,需要广泛而深入地学习多个领域的知识。这些课程不仅帮助建立扎实的编程基础,还培养了问题解决、算法设计、系统思维等多方面的能力。以下是一些核心的必修课: 计算机基础 计算机组成原理:理解计算机的硬件组…...

PHP时间相关函数
时间、日期 time()获取当前时间戳(10位)microtime(true)返回一个浮点时间戳data(格式,时间戳)日期格式化 $time time(); echo date(Y-m-d H:i:s, $time);strtotime&am…...

python进阶——python面向对象
前言 Python是一种面向对象的编程语言,可在Python中使用类和对象来组织和封装代码。面向对象编程(OOP)是一种编程范例,它将数据和操作数据的方法封装在一个对象内部,通过对象之间的交互来实现程序的功能。 1、面向对象…...

【无标题】vue2鼠标悬停(hover)时切换图片
在Vue 2中,要实现鼠标悬停(hover)时切换图片的功能,你不能直接在模板的:src绑定中处理这个逻辑,因为Vue的模板不支持条件渲染的复杂逻辑(如基于鼠标状态的动态图片切换)。但是,你可以…...
- 分析法)
每天一个数据分析题(四百五十九)- 分析法
故障树分析法经常与哪些方法联合使用? A. 头脑风暴法 B. 五问法 C. 配对法 D. 引力法 数据分析认证考试介绍:点击进入 题目来源于CDA模拟题库 点击此处获取答案 数据分析专项练习题库 内容涵盖Python,SQL,统计学…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
