使用太极taichi写一个只有一个三角形的有限元
公式来源
https://blog.csdn.net/weixin_43940314/article/details/128935230
GAME103
https://games-cn.org/games103-slides/
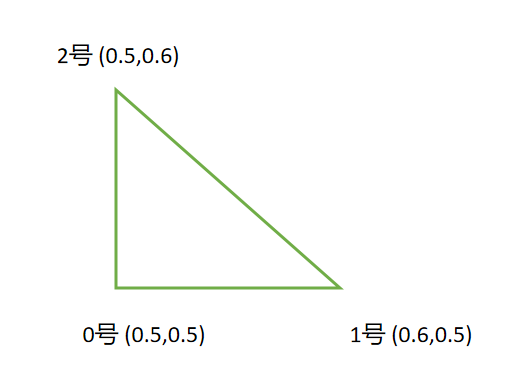
初始化我们的三角形
全局的坐标范围为0-1
我们的三角形如图所示
@ti.kernel
def init():X[0] = [0.5, 0.5]X[1] = [0.5, 0.6]X[2] = [0.6, 0.5]x[0] = X[0] + [0, 0.01]x[1] = X[1]x[2] = X[2]
X是rest pos
x是current pos
这里给一个小的增量是为了看出来被拉了,否则产生不了弹性力
公式抄录
[f1f2]=−ArefFS[X10X20]−T\begin{bmatrix} \mathbf{f_1} & \mathbf{f_2} \end{bmatrix}= -A^{ref} \mathbf{F} \mathbf{S } \begin{bmatrix} \mathbf{X_{10}} & \mathbf{X_{20}} \end{bmatrix}^{-T} [f1f2]=−ArefFS[X10X20]−T
F=[x10x20][X10X20]−1F=\begin{bmatrix} x_{10} & x_{20} \end{bmatrix}\begin{bmatrix} X_{10} & X_{20} \end{bmatrix}^{-1} F=[x10x20][X10X20]−1
S=2μG+λtrace(C)IS = 2 \mu G + \lambda trace(C) I S=2μG+λtrace(C)I
G=12(FTF−I)G = \frac{1}{2} (F^T F -I) G=21(FTF−I)
0. 设定一下材料参数
dim=2
n_particles = 3
n_elements = 1
area = 0.1*0.1*0.5
dt = 1e-4
E, nu = 1e3, 0.33 # Young's modulus and Poisson's ratio
mu, lam = E / 2 / (1 + nu), E * nu / (1 + nu) / (1 - 2 * nu) # Lame parameters
1 计算F
根据上面的公式,我们要先算F
@ti.kernel
def substep():#compute deformation gradientfor i in range(n_elements):Dm =ti.Matrix([[x[1][0]-x[0][0], x[2][0]-x[0][0]], [x[1][1]-x[0][1], x[2][1]-x[0][1]]])Dm_inv[i] = Dm.inverse()Ds = ti.Matrix([[X[1][0]-X[0][0], X[2][0]-X[0][0]], [X[1][1]-X[0][1], X[2][1]-X[0][1]]])F[i] = Ds @ Dm_inv[i]
2 计算格林应变
#compute green strain
for i in range(n_elements):G[i] = 0.5 * (F[i].transpose() @ F[i] - ti.Matrix([[1, 0], [0, 1]]))
3 计算PK1
#compute second Piola Kirchhoff stress
for i in range(n_elements):S[i] = 2 * mu *G[i] + lam * (G[i][0,0]+G[i][1,1]) * ti.Matrix([[1, 0], [0, 1]])
4 计算粒子上的力
#compute force(先暂且就计算一个三角形的力,后面再考虑多个三角形的情况)
force_matrix = F[0] @ S[0] @ Dm_inv[0].transpose() * area
force[1] = ti.Vector([force_matrix[0, 0], force_matrix[1, 0]])
force[2] = ti.Vector([force_matrix[0, 1], force_matrix[1, 1]])
force[0] = -force[1] - force[2]
5 加个重力
#gravityfor i in range(n_particles):force[i][1] -= 0.16 时间积分 同时处理边界条件
#time integration(with boundary condition)eps = 0.01for i in range(n_particles):vel[i] += dt * force[i]#boundary conditioncond = (x[i] < eps) & (vel[i] < 0) | (x[i] > 1) & (vel[i] > eps)for j in ti.static(range(dim)):if cond[j]:vel[i][j] = 0 x[i] += dt * vel[i]
完整的程序
# ref: https://blog.csdn.net/weixin_43940314/article/details/128935230import taichi as ti
import numpy as npti.init(arch=ti.cpu, debug=True)dim=2
n_particles = 3
n_elements = 1
area = 0.1*0.1*0.5
# lam = 1
# mu = 1
dt = 1e-4
E, nu = 1e3, 0.33 # Young's modulus and Poisson's ratio
mu, lam = E / 2 / (1 + nu), E * nu / (1 + nu) / (1 - 2 * nu) # Lame parametersx = ti.Vector.field(dim, dtype=float, shape=n_particles) #deformed position
force = ti.Vector.field(dim, dtype=float, shape=n_particles)
vel = ti.Vector.field(dim, dtype=float, shape=n_particles)
X = ti.Vector.field(dim, dtype=float, shape=n_particles) #undeformed position
S = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #Second Piola Kirchhoff stress
F = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #deformation gradient
G = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements) #green strain@ti.kernel
def init():X[0] = [0.5, 0.5]X[1] = [0.5, 0.6]X[2] = [0.6, 0.5]x[0] = X[0] + [0, 0.01]x[1] = X[1]x[2] = X[2]Dm_inv = ti.Matrix.field(n=dim, m=dim, dtype=float, shape=n_elements)
@ti.kernel
def substep():#compute deformation gradientfor i in range(n_elements):Dm =ti.Matrix([[x[1][0]-x[0][0], x[2][0]-x[0][0]], [x[1][1]-x[0][1], x[2][1]-x[0][1]]])Dm_inv[i] = Dm.inverse()Ds = ti.Matrix([[X[1][0]-X[0][0], X[2][0]-X[0][0]], [X[1][1]-X[0][1], X[2][1]-X[0][1]]])F[i] = Ds @ Dm_inv[i]# print(F[0])#compute green strainfor i in range(n_elements):G[i] = 0.5 * (F[i].transpose() @ F[i] - ti.Matrix([[1, 0], [0, 1]]))#compute second Piola Kirchhoff stressfor i in range(n_elements):S[i] = 2 * mu *G[i] + lam * (G[i][0,0]+G[i][1,1]) * ti.Matrix([[1, 0], [0, 1]])#compute force(先暂且就计算一个三角形的力,后面再考虑多个三角形的情况)force_matrix = F[0] @ S[0] @ Dm_inv[0].transpose() * areaforce[1] = ti.Vector([force_matrix[0, 0], force_matrix[1, 0]])force[2] = ti.Vector([force_matrix[0, 1], force_matrix[1, 1]])force[0] = -force[1] - force[2]# print(force[0])#gravityfor i in range(n_particles):force[i][1] -= 0.1#time integration(with boundary condition)eps = 0.01for i in range(n_particles):vel[i] += dt * force[i]#boundary conditioncond = (x[i] < eps) & (vel[i] < 0) | (x[i] > 1) & (vel[i] > eps)for j in ti.static(range(dim)):if cond[j]:vel[i][j] = 0 x[i] += dt * vel[i]def main():init()gui = ti.GUI('my', (1024, 1024))while gui.running:for e in gui.get_events():if e.key == gui.ESCAPE:gui.running = Falseelif e.key == 'r':init()for i in range(30):substep()vertices_ = np.array([[0, 1, 2]], dtype=np.int32)particle_pos = x.to_numpy()a = vertices_.reshape(n_elements * 3)b = np.roll(vertices_, shift=1, axis=1).reshape(n_elements * 3)gui.lines(particle_pos[a], particle_pos[b], radius=1, color=0x4FB99F)gui.circles(particle_pos, radius=5, color=0xF2B134)gui.show()if __name__ == '__main__':main()

相关文章:

使用太极taichi写一个只有一个三角形的有限元
公式来源 https://blog.csdn.net/weixin_43940314/article/details/128935230 GAME103 https://games-cn.org/games103-slides/ 初始化我们的三角形 全局的坐标范围为0-1 我们的三角形如图所示 ti.kernel def init():X[0] [0.5, 0.5]X[1] [0.5, 0.6]X[2] [0.6, 0.5]x[0…...
进程,线程
进程是操作系统分配资源的基本单位,线程是CPU调度的基本单位。 PCB:进程控制块,操作系统描述程序的运行状态,通过结构体task,struct{…},统称为PCB(process control block)。是进程管理和控制的…...

第03章_基本的SELECT语句
第03章_基本的SELECT语句 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 1. SQL概述 1.1 SQL背景知识 1946 年,世界上第一台电脑诞生,如今,借由这台电脑发展…...

干货 | 简单了解运算放大器...
运算放大器发明至今已有数十年的历史,从最早的真空管演变为如今的集成电路,它在不同的电子产品中一直发挥着举足轻重的作用。而现如今信息家电、手机、PDA、网络等新兴应用的兴起更是将运算放大器推向了一个新的高度。01 运算放大器简述运算放大器&#…...
C++定位new用法及注意事项
使用定位new创建对象,显式调用析构函数是必须的,这是析构函数必须被显式调用的少数情形之一!, 另有一点!!!析构函数的调用必须与对象的构造顺序相反!切记!!&a…...

【Android笔记75】Android之翻页标签栏PagerTabStrip组件介绍及其使用
这篇文章,主要介绍Android之翻页标签栏PagerTabStrip组件及其使用。 目录 一、PagerTabStrip翻页标签栏 1.1、PagerTabStrip介绍 1.2、PagerTabStrip的使用 (1)创建布局文件...

【Kafka】【二】消息队列的流派
消息队列的流派 ⽬前消息队列的中间件选型有很多种: rabbitMQ:内部的可玩性(功能性)是⾮常强的rocketMQ: 阿⾥内部⼀个⼤神,根据kafka的内部执⾏原理,⼿写的⼀个消息队列中间 件。性能是与Kaf…...

现代 cmake (cmake 3.x) 操作大全
cmake 是一个跨平台编译工具,它面向各种平台提供适配的编译系统配置文件,进而调用这些编译系统完成编译工作。cmake 进入3.x 版本,指令大量更新,一些老的指令开始被新的指令集替代,并加入了一些更加高效的指令/参数。本…...
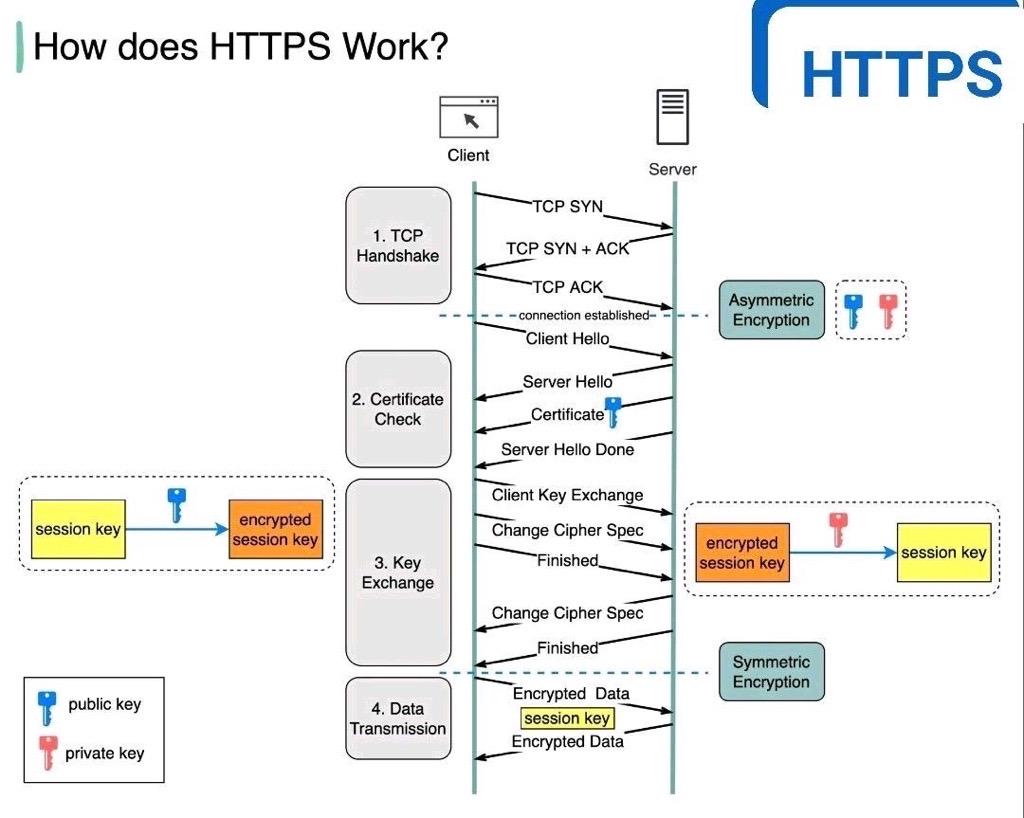
how https works?https工作原理
简单一句话: https http TLShttps 工作原理:HTTPS (Hypertext Transfer Protocol Secure)是一种带有安全性的通信协议,用于在互联网上传输信息。它通过使用加密来保护数据的隐私和完整性。下面是 HTTPS 的工作原理:初始化安全会…...

Docker的资源控制管理
目录 一、CPU控制 1、设置CPU使用率上限 2、设置CPU资源占用比(设置多个容器时才有效) 3、设置容器绑定指定的CPU 二、对内存使用进行限制 1、创建指定物理内存的容器 2、创建指定物理内存和swap的容器 3、 对磁盘IO配额控制(blkio&a…...

MMSeg无法使用单类自定义数据集训练
文章首发及后续更新:https://mwhls.top/4423.html,无图/无目录/格式错误/更多相关请至首发页查看。 新的更新内容请到mwhls.top查看。 欢迎提出任何疑问及批评,非常感谢! 摘要:将三通道图像转为一通道图像,…...

Redis使用方式
一、Redis基础部分: 1、redis介绍与安装比mysql快10倍以上 *****************redis适用场合**************** 1.取最新N个数据的操作 2.排行榜应用,取TOP N 操作 3.需要精确设定过期时间的应用 4.计数器应用 5.Uniq操作,获取某段时间所有数据排重值 6.实时系统,反垃圾系统7.P…...
 枪械名 红字效果 元素属性 清图评分 Boss战评分 泛用性评分 特殊性评分 最终评级 掉落点 掉率 图片 瘟疫传播)
无主之地3重型武器节奏评分榜(9.25) 枪械名 红字效果 元素属性 清图评分 Boss战评分 泛用性评分 特殊性评分 最终评级 掉落点 掉率 图片 瘟疫传播
无主之地3重型武器节奏评分榜(9.25) 枪械名 红字效果 元素属性 清图评分 Boss战评分 泛用性评分 特殊性评分 最终评级 掉落点 掉率 图片 瘟疫传播者 发射巨大能量球,能量球会额外生成追踪附近敌人的伴生弹 全属性 SSS SSS SSS - T0 伊甸6号-…...

什么是编程什么是算法
1.绪论 编程应在一个开发环境中完成源程序的编译和运行。首先,发现高级语言开发环境,TC,Windows系统的C++,R语言更适合数学专业的学生。然后学习掌握编程的方法,在学校学习,有时间的人可以在网上学习,或者购买教材自学。最后,编写源程序,并且在开发环境中实践。 例如…...

【c++】函数
文章目录函数的定义函数的调用值传递常见样式函数的声明函数的分文件编写函数的作用: 将一段经常使用的代码封装起来,减少重复代码。 一个较大的程序,一般分为若干个程序块,每个模板实现特定的功能。 函数的定义 返回值类型 函数…...

[golang gin框架] 1.Gin环境搭建,程序的热加载,路由GET,POST,PUT,DELETE
一.Gin 介绍Gin 是一个 Go (Golang) 编写的轻量级 http web 框架,运行速度非常快,如果你是性能和高效的追求者,推荐你使用 Gin 框架.Gin 最擅长的就是 Api 接口的高并发,如果项目的规模不大,业务相对简单,这…...
【开源】祁启云网络验证系统V1.11
简介 祁启云免费验证系统 一个使用golang语言、Web框架beego、前端Naive-Ui-Admin开发的免费网络验证系统 版本 当前版本1.11 更新方法 请直接将本目录中的verification.exe/verification直接覆盖到你服务器部署的目录,更新前,请先关闭正在运行的验…...

震源机制(Focal Mechanisms)之沙滩球(Bench Ball)
沙滩球包含如下信息: a - 判断断层类型,可根据球的颜色快速判断 b - 判断断层的走向(strike),倾角(dip) c - 确定滑移角/滑动角(rake) 走向 ,倾角,滑移角 如不了解断层的定义,可以先阅读:震…...

C++入门:多态
多态按字面的意思就是多种形态。当类之间存在层次结构,并且类之间是通过继承关联时,就会用到多态。C 多态意味着调用成员函数时,会根据调用函数的对象的类型来执行不同的函数。1、纯虚函数声明如下: virtual void funtion1()0; 纯…...
(C++实现))
华为OD真题_工位序列统计友好度最大值(100分)(C++实现)
题目描述 工位由序列F1,F2…Fn组成,Fi值为0、1或2。其中0代表空置,1代表有人,2代表障碍物。 1、某一空位的友好度为左右连续老员工数之和 2、为方便新员工学习求助,优先安排友好度高的空位 给出工位序列,求所有空位中友好度的最大值。 输入描述 第一行为工位序列:F1,F…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
