数据结构之数组
写在前面
看下数组。
1:巴拉巴拉
数组是一种线性数据结构,使用连续的内存空间来存储数据,存储的数据要求有相同的数据类型,并且每个元素占用的内存空间相同。获取元素速度非常快,为O(1)常量时间复杂度,所以数组在我们工作直接或者是间接的用到还是比较多的。
2:代码
定义接口:
package com.dahuyou.datastructure.arraylist;public interface List<E> {/*** Appends the specified element to the end of this list (optional* operation).* <p>* 追加元素到尾部!*/boolean add(E e);/*** Removes the element at the specified position in this list (optional* operation). Shifts any subsequent elements to the left (subtracts one* from their indices). Returns the element that was removed from the* list.** 删除指定位置的元素**/E remove(int index);/*** Returns the element at the specified position in this list.** 返回指定位置的元素*/E get(int index);}
实现类,这里不贴所有代码了,只看下重要的方法。
- add
@Override
public boolean add(E e) {// 确保内部容量int minCapacity = size + 1;if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);}// 判断扩容操作,即将满时扩容,扩容为原来的1.5倍,直接通过oldCapacity + (oldCapacity >> 1)移位操作完成,效率高if (minCapacity - elementData.length > 0) {int oldCapacity = elementData.length;int newCapacity = oldCapacity + (oldCapacity >> 1);if (newCapacity - minCapacity < 0) {newCapacity = minCapacity;}elementData = Arrays.copyOf(elementData, newCapacity);}// 添加元素elementData[size++] = e;return true;
}
这里在两种情况下会进行扩容,第一次插入元素时扩容到10,之后元素满时扩容到原来的1.5倍,这里使用了移位运算,效率更高。
- remove
@Override
public E remove(int index) {E oldValue = (E) elementData[index];int numMoved = size - index - 1;if (numMoved > 0) {// 从原始数组的某个位置,拷贝到目标对象的某个位置开始后n个元素System.arraycopy(elementData, index + 1, elementData, index, numMoved);}elementData[--size] = null; // clear to let GC do its workreturn oldValue;
}
注意这里删除元素并不是通过一个一个的交换元素来实现的,而是直接通过native方法java.lang.System#arraycopy:
public static native void arraycopy(Object src, int srcPos,Object dest, int destPos,int length);
因为是底层直接操作内存,所以效率更高。
测试:
package com.dahuyou.datastructure.arraylist;public class TT {public static void main(String[] args) {List<String> list = new ArrayList<>();list.add("01");list.add("02");list.add("03");list.add("04");list.add("05");list.add("06");list.add("07");list.add("08");list.add("09");list.add("10");list.add("11");list.add("12");System.out.println(list);list.remove(9);System.out.println(list);}}
运行:
ArrayList{elementData=[01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, null, null, null], size=12}
ArrayList{elementData=[01, 02, 03, 04, 05, 06, 07, 08, 09, 11, 12, null, null, null, null], size=11}Process finished with exit code 0
写在后面
参考文章列表
相关文章:

数据结构之数组
写在前面 看下数组。 1:巴拉巴拉 数组是一种线性数据结构,使用连续的内存空间来存储数据,存储的数据要求有相同的数据类型,并且每个元素占用的内存空间相同。获取元素速度非常快,为O(1)常量时间复杂度,所…...

springboot集成sensitive-word实现敏感词过滤
文章目录 敏感词过滤方案一:正则表达式方案二:基于DFA算法的敏感词过滤工具框架-sensitive-wordspringboot集成sensitive-word步骤一:引入pom步骤二:自定义配置步骤三:自定义敏感词白名单步骤四:核心方法测…...

C++ 之动手写 Reactor 服务器模型(一):网络编程基础复习总结
基础 IP 地址可以在网络环境中唯一标识一台主机。 端口号可以在主机中唯一标识一个进程。 所以在网络环境中唯一标识一个进程可以使用 IP 地址与端口号 Port 。 字节序 TCP/IP协议规定,网络数据流应采用大端字节序。 大端:低地址存高位,…...

qt 在vs2022 报错记录
1,qt.network.ssl: QSslSocket::connectToHostEncrypted: TLS initialization failed 需要把SSL 相关的库加入进去,如ssleay32.dll,libeay32.dll。 2,在一个文件中已定义,编译器在链接时,在多处报 已在.*…...

【人工智能】TensorFlow和机器学习概述
一、TensorFlow概述 TensorFlow是由Google Brain团队开发的开源机器学习库,用于各种复杂的数学计算,特别是在深度学习领域。以下是对TensorFlow的详细概述: 1. 核心概念 张量(Tensor):TensorFlow中的基本…...

SQLALchemy 的介绍
SQLALchemy 的介绍 基本概述主要特点使用场景安装与配置安装 SQLAlchemy配置 SQLAlchemy示例:使用 SQLite 数据库连接到其他数据库 结论 总结 SQLAlchemy是Python编程语言下的一款开源软件,它提供了SQL工具包及对象关系映射(ORM)工…...
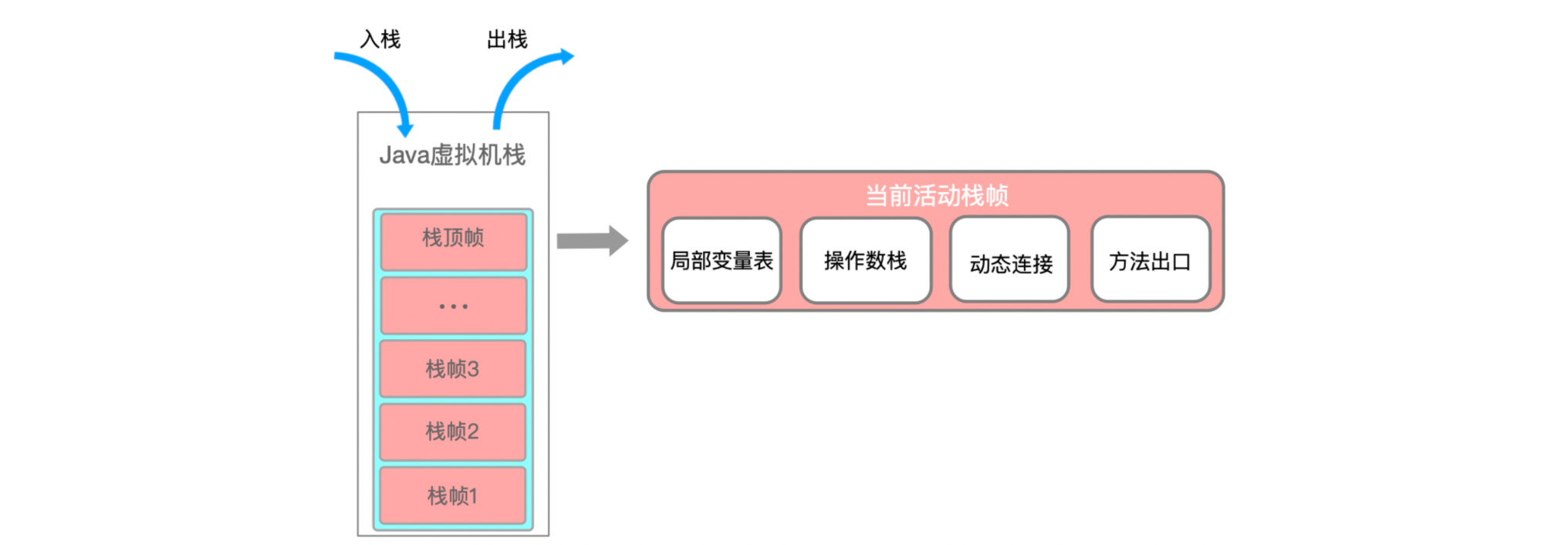
Java虚拟机:运行时内存结构
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 035 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

微信小程序子组件调用父组件的方法
来源:通义千文2.5 步骤 1: 定义父组件中的方法 首先,在父组件中定义一个方法(如 handleClick),并准备一个用于接收子组件传来的数据的方法。 父组件(Parent.wxml) html<!-- parent.wxml …...

【数据结构】TreeMap和TreeSet
目录 前言TreeMap实现的接口内部类常用方法 TreeSet实现的接口常用方法 前言 Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。 一般把搜索的数据称为关键字(Key), 和关键字对应的称为…...

前端react集成OIDC
文章目录 OpenID Connect (OIDC)3种 授权模式 【服务端】express 集成OIDC【前端】react 集成OIDCoidc-client-js库 原生集成react-oidc-context 库非组件获取user信息 OAuth 2.0 协议主要用于资源授权。 OpenID Connect (OIDC) https://openid.net/specs/openid-connect-core…...

JavaWeb—XML_Tomcat10_HTTP
一、XML XML是EXtensible MarkupLanguage的缩写,翻译过来就是可扩展标记语言。所以很明显,XML和HTML一样都是标记语言,也就是说它们的基本语法都是标签。 可扩展:三个字表面上的意思是XML允许自定义格式。但这不代表你可以随便写; 在XML基…...

中介者模式在Java中的实现:设计模式精解
中介者模式在Java中的实现:设计模式精解 中介者模式(Mediator Pattern)是一种行为型设计模式,用于定义一个中介者对象,以封装一系列对象之间的交互,从而使对象之间的交互不再直接发生,减少了系…...

PyQt编程快速上手
Python GUI安装 GUI就是图形用户界面的意思,在Python中使用PyQt可以快速搭建自己的应用,使得自己的程序看上去更加高大上,学会GUI编程可以使得自己的软件有可视化的结果。 如果你想用Python快速制作界面,可以安装PyQt:…...

Docker Swarm管理
Docker Swarm管理 前置知识点 Docker Swarm 是 Docker 公司 2014年出品的基于 Docker 的集群管理调度工具,能够将多台主机构建成一个Docker集群,并结合Overlay网络实现容器调度的互访 用户可以只通过 Swarm API 来管理多个主机上的 Docker Swarm 群集包…...

Python | Leetcode Python题解之第335题路径交叉
题目: 题解: class Solution:def isSelfCrossing(self, distance: List[int]) -> bool:n len(distance)# 处理第 1 种情况i 0while i < n and (i < 2 or distance[i] > distance[i - 2]):i 1if i n:return False# 处理第 j 次移动的情况…...

Ubuntu视频工具
1. VLC VLC Media Player(VLC多媒体播放器),最初命名为VideoLAN客户端,是VideoLAN品牌产品,是VideoLAN计划的多媒体播放器。它支持众多音频与视频解码器及文件格式,并支持DVD影音光盘,VCD影音光…...

HBase snapshot+replication 测试
一、背景 画像标签服务(CDP)是核心服务,被公司其他系统如现金、电商、风控等核心业务调用。异常的话,影响范围大。 二、目标 存量数据测试通过 snapshot 迁移。增量数据测试通过 replication 同步。 三、测试 方案二测试&#x…...

代码随想录算法训练营第四十一天|图论基础、深度优先搜索理论基础、98. 所有可达路径、797. 所有可能的路径
图论基础 图的种类:有向图 和 无向图,加权有向图, 加权无向图 无向图中有几条边连接该节点,该节点就有几度。 在有向图中,每个节点有出度和入度。出度:从该节点出发的边的个数。入度:指向该节…...

STM32学习笔记09-SPI通信
目录 SPI通信简介 硬件电路 移位示意图 SPI基本时序单元 SPI时序 W25Q64简介 硬件电路 W25Q64框图 Flash操作注意事项 SPI外设简介 SPI框图 SPI基本结构 主模式全双工连续传输 非连续传输 软件/硬件波形对比 SPI应用 软件SPI读写W25Q64 硬件SPI读写W25Q64 SP…...

树------二叉树
什么是树: 树是一种特殊的结构,由多个节点连接构成,并且不包含回路,也可以认为树是不包含回路的无向连通图,具体如下图所示。 当我们要确定一棵树的形态时,要指定一个根节点,没有父亲节点的节点…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
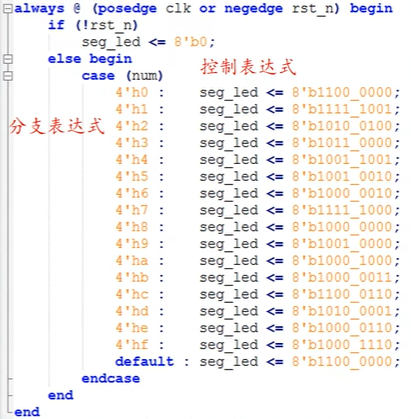
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...
