Matlab傅里叶谱方法求解二维波动方程
傅里叶谱方法求解基本偏微分方程—二维波动方程
二维波动方程
将一维波动方程中的一维无界弦自由振动方程推广到二维空间上, 就得到了描述无界 (−∞<x,y<∞)(-\infty<x, y<\infty)(−∞<x,y<∞) 弹性薄膜的波动方程:
∂2u∂t2=a2(∂2∂x2+∂2∂y2)u(1)\frac{\partial^2 u}{\partial t^2}=a^2\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u \tag{1} ∂t2∂2u=a2(∂x2∂2+∂y2∂2)u(1)
取 a=1a=1a=1, 初始条件为:
u∣t=0=e−20[(x−0.4)2+(y+0.4)2]+e−20[(x+0.4)2+(y−0.4)2],∂u∂t∣t=0=0(2)\left.u\right|_{t=0}=\mathrm{e}^{-20\left[(x-0.4)^2+(y+0.4)^2\right]}+\mathrm{e}^{-20\left[(x+0.4)^2+(y-0.4)^2\right]},\left.\quad \frac{\partial u}{\partial t}\right|_{t=0}=0 \tag{2} u∣t=0=e−20[(x−0.4)2+(y+0.4)2]+e−20[(x+0.4)2+(y−0.4)2],∂t∂ut=0=0(2)
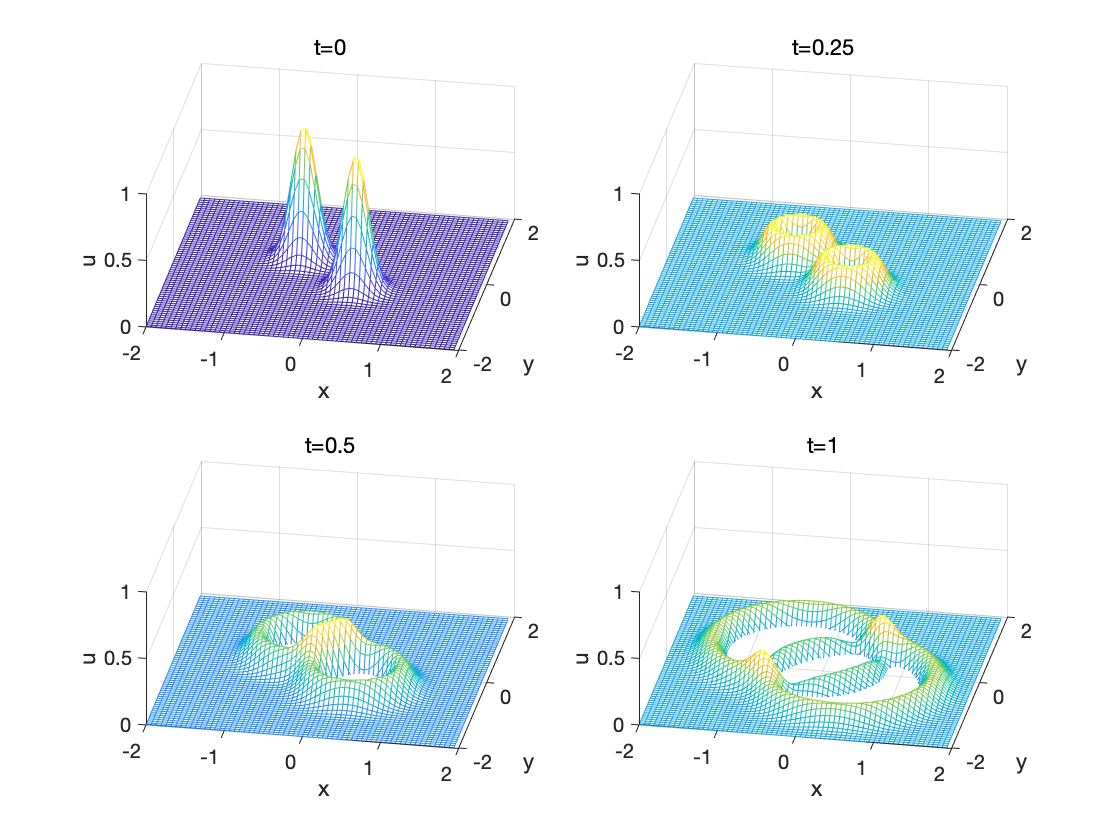
可以这样理解上述初始条件的物理意义: 两手抓住弹性薄膜的两个位置, 分别提起, 使薄膜上形成两个峰, 在 t=0t=0t=0 时刻突然松手。根据生活常识可以预料到, 这两个位置的薄 膜将来回振动, 与此同时, 产生的波向四周传播, 而且波与波会在相遇处叠加。
为便于求解, 引入函数 vvv 对式 (1)(1)(1) 进行降阶, 得:
{∂u∂t=v∂v∂t=a2(∂2∂x2+∂2∂y2)u(3)\left\{\begin{array}{l} \frac{\partial u}{\partial t}=v \\ \frac{\partial v}{\partial t}=a^2\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) u \end{array}\right. \tag{3} {∂t∂u=v∂t∂v=a2(∂x2∂2+∂y2∂2)u(3)
对上式等号两边做傅里叶变换, 得到常微分方程组:
{∂u~^∂t=v^^∂v^^∂t=−a2(kx2+ky2)u^^(4)\left\{\begin{array}{l} \frac{\partial \hat{\tilde{u}}}{\partial t}=\hat{\hat{v}} \\ \frac{\partial \hat{\hat{v}}}{\partial t}=-a^2\left(k_x^2+k_y^2\right) \hat{\hat{u}} \end{array}\right. \tag{4} {∂t∂u~^=v^^∂t∂v^^=−a2(kx2+ky2)u^^(4)
接下来用 ode45 求解即可, 代码如下:
主程序代码如下:
clear all; close all;L=4;N=64;
x=L/N*[-N/2:N/2-1];y=x;
kx=(2*pi/L)*[0:N/2-1 -N/2:-1];ky=kx;
[X,Y]=meshgrid(x,y);
[kX,kY]=meshgrid(kx,ky);
K2=kX.^2+kY.^2;
% 初始条件
u=exp(-20*((X-0.4).^2+(Y+0.4).^2))+exp(-20*((X+0.4).^2+(Y-0.4).^2));
ut=fft2(u);vt=zeros(N);uvt=[ut(:); vt(:)];
% 求解
a=1;t=[0 0.25 0.5 1];
[t,uvtsol]=ode45('wave2D',t,uvt,[],N,K2(:),a);
% 画图
for n=1:4subplot(2,2,n)mesh(x,y,ifft2(reshape(uvtsol(n,1:N^2),N,N))),view(10,45)title(['t=' num2str(t(n))]),axis([-L/2 L/2 -L/2 L/2 0 1])xlabel x,ylabel y,xlabel x,zlabel u
end文件 wave1D.m 代码如下:
function duvt=wave2D(t,uvt,dummy,N,K2,a)
ut=uvt(1:N^2);vt=uvt(N^2+[1:N^2]);
duvt=[vt;-a^2*K2.*ut];
end
程序输出结果如图所示, 它反映了弹性薄膜上的波向四周传播的过程。
相关文章:

Matlab傅里叶谱方法求解二维波动方程
傅里叶谱方法求解基本偏微分方程—二维波动方程 二维波动方程 将一维波动方程中的一维无界弦自由振动方程推广到二维空间上, 就得到了描述无界 (−∞<x,y<∞)(-\infty<x, y<\infty)(−∞<x,y<∞) 弹性薄膜的波动方程: ∂2u∂t2a2(∂2∂x2∂2∂y2)u(1)\frac…...

【深度学习】卷积神经网络
1 卷积神经网络(CNN)可以做什么? 检测任务分类与检索超分辨率重构:将图像训练的更清晰医学任务等无人驾驶人脸识别 2 用GPU:图像处理单元 比CPU块一百倍以上 3 卷积神经网络与传统神经网络的区别 传统神经网络&…...
【C++】六个默认成员函数——取地址重载,const成员函数
🍅 初始化和清理 拷贝复制 目录 ☃️1.取地址重载 ☃️2.const取地址操作符重载 这两个运算符一般不需要重载,使用编译器生成的默认取地址的重载即可,只有特殊情况,才需要重载,比如想让别人获取到指定的内容…...
Win11浏览器无法上网,秒杀网上99.9%教程—亲测完胜
前言 例如:网上的教程 列如: 关闭代理服务器、QQ微信可以登录,但浏览器无法上网、Win11、Win10无法上网、重启网络、重启电脑、去掉代理服务器等等。 一系列教程,要多鸡肋就多鸡肋。 我是用我2020年在CSDN上发布的第一篇文章&…...
)
Vulkan Graphics pipeline Dynamic State(图形管线之动态状态)
Vulkan官方英文原文:请见 Vulkan 1.3.236 - A Specification 10.9 章节。对应的Vulkan技术规格说明书版本: Vulkan 1.3.2A dynamic pipeline state is a state that can be changed by a command buffer command during the execution of a command buff…...

CSP-《I‘m stuck!》-感悟
题目 做题过程 注:黄色高亮表示需要注意的地方,蓝色粗体表示代码思路 好久没有写过代码了,今天做这道编程题,简直是灾难现场。 上午编程完后发现样例没有通过,检查发现算法思路出现了问题:我计数了S不能到…...
)
[实践篇]13.19 Qnx进程管理slm学习笔记(二)
【QNX Hypervisor 2.2用户手册】目录(完结) 四,配置文件结构 4.1 根元素 一个配置文件的XML根元素是system,如下: <SLM:system>-- component and module descriptions -- </SLM:system> 4.2 组件 一个进程对于SLM来说就是一个组件。在配置文件中,你必须为一…...
(免费分享)基于 SpringBoot 的高校宿舍管理系统带论文
项目描述 系统代码质量高,功能强大,带论文。 系统的功能主要有: (1)基本信息管理 基本信息分为学生信息和宿舍信息两部分,其功能是负责维护这些信息,对 它们进行增删查改等操作。 &#x…...

运筹系列78:cbc使用介绍
1. 上手 1.1 快速使用 首先是简单的调用测试,在mac上首先安装clp的库:brew install coin-or-tools/coinor/cbc,然后新建项目进行调用,各项配置如下,注意要添加的library和directory比较多: 1.2 命令行方…...

RocketMQ底层源码解析——事务消息的实现
1. 简介 RocketMQ自身实现了事务消息,可以通过这个机制来实现一些对数据一致性有强需求的场景,保证上下游数据的一致性。 以电商交易场景为例,用户支付订单这一核心操作的同时会涉及到下游物流发货、积分变更、购物车状态清空等多个子系统…...

学习802.11之MAC帧格式(一篇就够!)
802.11规范的关键在于MAC(媒介访问控制层),MAC位于各式物理层之上,控制数据传输。负责核心成帧操作以及与有线骨干网络之间的交互。 802.11 MAC采用载波监听多路访问(CSMA)机制来控制对传输媒介的访问&…...

使用阿里云IoT Studio建立物模型可视化界面
使用阿里云IoT Studio建立物模型可视化界面 上一篇文章介绍了如何使用ESP-01S上报数据到物模型:https://blog.csdn.net/weixin_46251230/article/details/128996719 这次使用阿里云IoT Studio建立物模型的Web页面 阿里云IoT Studio: https://studio.i…...

HBase 复习 ---- chapter07
HBase 复习 ---- chapter07部署 HBase(运维) 1:部署 HBase 实际是部署了三个技术(hadoop zookeeper hbase) hadoop hdfs mapreduce common hdfs namenode datanode secondaryNamenode yarn ResourceManager&a…...

跟我一起写Makefile--个人总结
此篇笔记是根据陈皓大佬《跟我一起写Makefile》学习所得 文章目录换行符clean变量make的自动推导另类风格的Makefile清空目标文件的规则cleanMakefile总述显示规则隐晦规则变量的定义注释引用其它的Makefile环境变量MAKEFILESmake的工作方式书写规则规则举例规则的语法在规则中…...

设计模式之为什么要学好设计模式
目录1 回顾软件设计原则2 设计模式总览3 经典框架都在用设计模式解决问题1 回顾软件设计原则 不用设计模式并非不可以,但是用好设计模式能帮助我们更好地解决实际问题,设计模式最重要的是解耦。设计模式天天都在用,但自己却无感知。我们把设…...
大数据时代的小数据神器 - asqlcell
自从Google发布了经典的MapReduce论文,以及Yahoo开源了Hadoop的实现,大数据这个词就成为了一个行业的热门。在不断提高的机器性能和各种层出不穷的工具框架加持下,数据分析开始从过去的采样抽查变成全量整体,原先被抽样丢弃的隐藏…...
【呕心沥血】整理全栈自动化测试技术(三):如何编写技术方案
前面两篇笔记我介绍了自动化测试前期调研注意事项和前置准备阶段切入点,有同学在后台提问: “做完前期的调研和准备工作,领导要求写一个落地方案并评审,自动化测试的落地方案该怎么写”? 首先这个要求我觉得挺正常&a…...
67. 二进制求和
文章目录题目描述竖式模拟转换为十进制计算题目描述 给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 示例 1: 输入:a “11”, b “1” 输出:“100” 示例 2: 输入:a “1010”, b “1011” …...
)
1555数列极差(队列 优先队列 )
目录 题目描述 解题思路 代码部分 题目描述 在黑板上写了N个正整数作成的一个数列,进行如下操作:每一次擦去其中的两个数a和b,然后在数列中加入一个数a*b1,如此下去直至黑板上剩下一个数,在所有按这种操作方式最后得…...
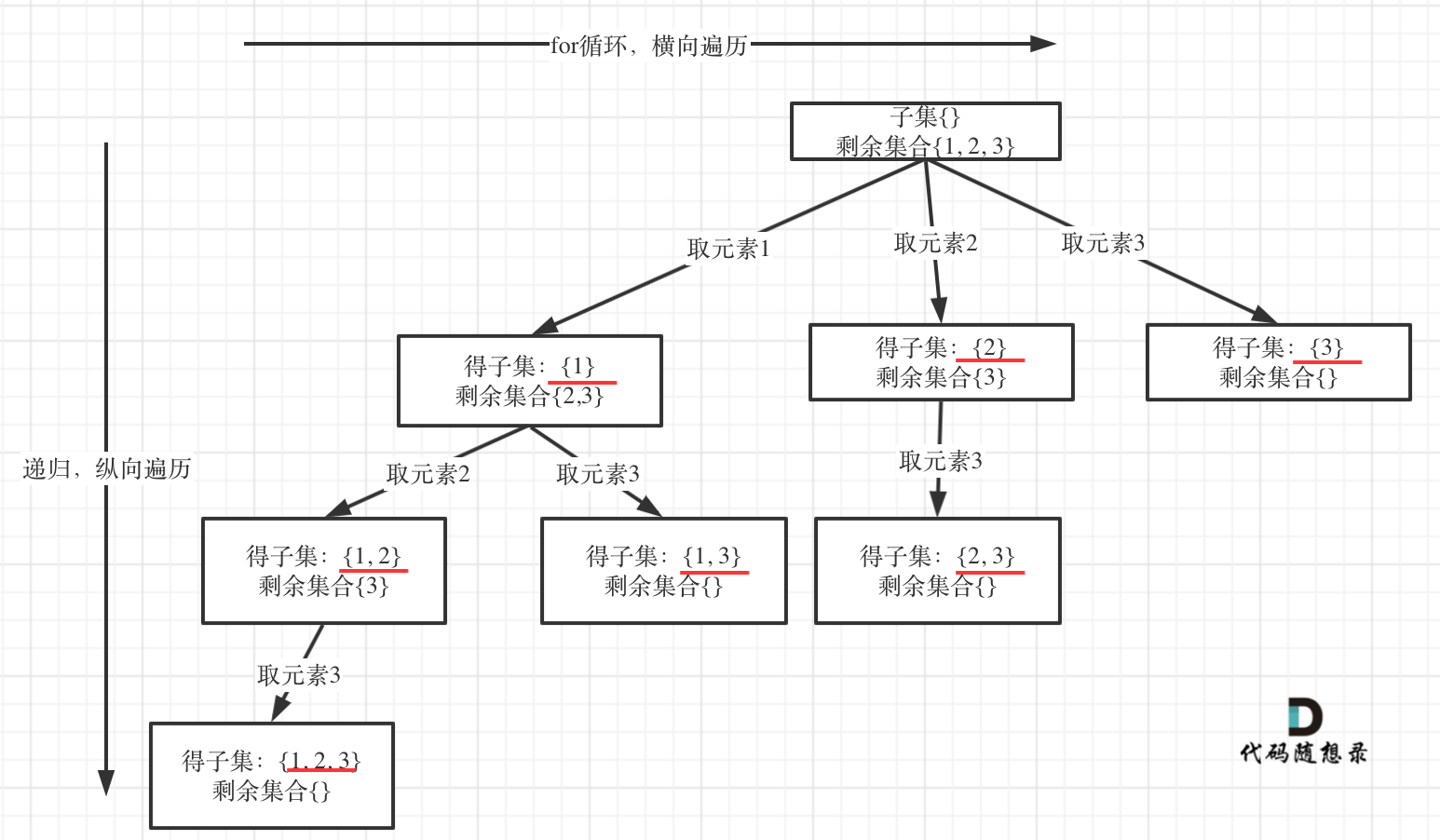
代码随想录算法训练营第二十七天 | 93.复原IP地址,78.子集,90.子集II
一、参考资料复原IP地址题目链接/文章讲解:https://programmercarl.com/0093.%E5%A4%8D%E5%8E%9FIP%E5%9C%B0%E5%9D%80.html 视频讲解:https://www.bilibili.com/video/BV1XP4y1U73i/子集题目链接/文章讲解:https://programmercarl.com/0078.…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
