4章10节:用R做数据重塑,变体函数应用详解和可视化的数据预处理介绍
数据重塑(Data Reshaping)是将数据从一种结构转换为另一种结构的过程,是清理、分析和可视化数据的重要步骤。R语言作为数据科学的强大工具,提供了许多包来帮助我们进行数据重塑,其中最常用的就是
dplyr包。dplyr包以其简洁的语法和高效的操作速度著称,它不仅可以帮助我们进行数据筛选、变换、汇总等常规操作,还能够通过一系列变体函数来简化数据重塑的过程。本文将深入探讨这些变体函数的应用,帮助读者在实际工作中灵活处理各种数据重塑需求。
一、回顾dplyr包的常用应用
dplyr 是R语言中最常用的一个数据操作包,以其简洁、直观的语法和强大的功能而受到广大数据科学家的青睐。它能够高效地进行数据的选择、筛选、排序、变换、汇总等操作。常见的函数包括 select()、filter()、arrange()、mutate()、summarize() 等,这些函数可以与 %>%(管道操作符)组合使用,从而提高代码的可读性和编写效率。
然而,dplyr的强大并不仅限于这些基础函数。为应对更复杂的数据操作场景,dplyr 提供了三组变体函数,即 _all、_at、_if 后缀的函数。这些变体函数可以在数据框中选择性地对列进行操作,从而更加灵活和精确地处理数据。接下来,我们将深入探讨这些变体函数的具体用法和应用场景。
library(dplyr)# 加载示例数据集
data <- iris# 使用dplyr进行简单相关文章:

4章10节:用R做数据重塑,变体函数应用详解和可视化的数据预处理介绍
数据重塑(Data Reshaping)是将数据从一种结构转换为另一种结构的过程,是清理、分析和可视化数据的重要步骤。R语言作为数据科学的强大工具,提供了许多包来帮助我们进行数据重塑,其中最常用的就是dplyr包。dplyr包以其简洁的语法和高效的操作速度著称,它不仅可以帮助我们进…...

Socks5代理IP在跨境电商和网络爬虫领域的实战应用
在现代互联网环境中,Socks5代理IP因其强大的灵活性和隐私保护功能,成为了跨境电商和网络爬虫领域的重要工具。本文将探讨Socks5代理IP的基本原理,并详细介绍其在跨境电商和网络爬虫中的实际应用。 1. Socks5代理IP简介 Socks5代理IP是一种网…...

农业上的目标跟踪论文汇总
文章目录 2022Multi-object tracking using Deep SORT and modified CenterNet in cotton seedling counting (Computers and Electronics in Agriculture)A novel apple fruit detection and counting methodology based on deep learning and trunk tracking in modern orcha…...

gpxt 小程序:轨迹合并与管理的高效工具
引言 在户外探险和运动追踪领域,GPXT小程序以其独特的轨迹管理和合并功能脱颖而出,成为徒步、骑行等运动爱好者不可或缺的工具。本文将详细介绍GPXT小程序的核心功能及其对户外活动爱好者的实用性。 核心功能概览 轨迹合并 GPXT小程序允许用户将多个…...

elasticsearch集成springboot详细使用
1.es下载&配置 配置JVM 配置跨域 配置https和密码 2.es启动 .\elasticsearch.bat 或 后台启动: nohup ./bin/elasticsearch& 浏览器访问:https://localhost:9200 输入账户:elastic / 123456 3.重置es密码 .\elasticsearch-r…...

html+css网页制作 化妆品电商4个页面
htmlcss网页制作 化妆品电商4个页面 网页作品代码简单,可使用任意HTML编辑软件(如:Dreamweaver、HBuilder、Vscode 、Sublime 、Webstorm、Text 、Notepad 等任意html编辑软件进行运行及修改编辑等操作)。 获取源码 1ÿ…...

微调LLama 3.1——七月论文审稿GPT第5.5版:拿早期paper-review数据集微调LLama 3.1
前言 对于llama3,我们之前已经做了针对llama3 早7数据微调后的测评 去pk llama2的早7数据微调后,推理测试集中的早期paper:出来7方面review去pk gpt4推理测试集中的早期paper:7方面reviewground truth是早期paper的7方面人工rev…...

rust 编译时报错:type annotations needed for Box
如下图所示: 解决方法: 升级time的版本: cargo update -p time...
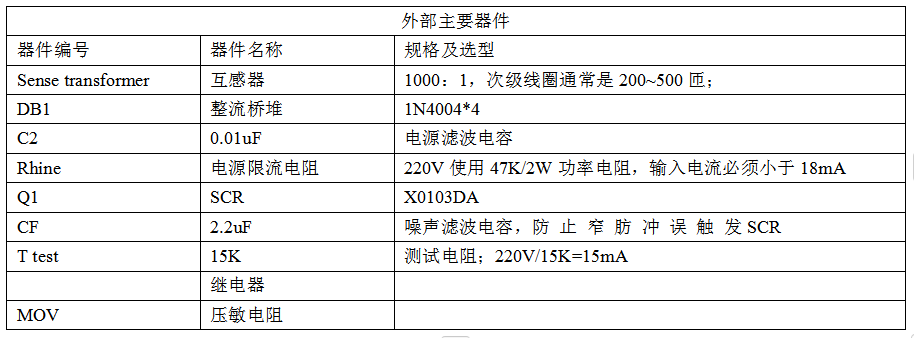
应用方案 | 低功耗接地故障控制器D4145
一、概述 D4145 是一个接地故障断路器。它能够检测到不良的接地条件,譬如装置接触到水时,它会在有害或致命的电击发生之前将电路断开。 D4145能检测并保护从火线到地线,从零线到地线的故障.这种简单而传统的电路设计能够确保其应用自如和长时间的可靠性。…...

第一次彩色pcb打样记录
感受和总结 看到彩色电路板和绿油板放在一起,感触还是挺大的。而且彩色板还直接给沉金,感觉焊上器件不要外壳都很好看了。后面一定记录一下这个板子实现的功能。 板子功能暂时分配 五个触摸盘,为了通过触摸控制不同功能,例如&a…...

通过 MediatR 实现了请求的分发和处理器的解耦
1. 前端请求发起 假设前端通过 HTTP GET 请求访问 GetTemplateSettings 端点,URL 中包含了 SubjectUuid 和 SubjectType 作为查询参数。 2. 进入 Controller 方法 请求到达后,会进入 MinBcController 类中的 GetTemplateSettings 方法,该方…...

Naive UI+vue一些组件的注意事项
NSpace(间距 Space) 默认给出space内的组件加一个div间隔,只能批量修改space内的元素样式,不能单独修改自组件样式,一般用于横向布局,若垂直布局若需要flex布局,慎用space组件NDataTable(数据表格 Data Table) :flex-h…...

sgetrf M N is 103040 时报错,这是个bug么 lapack and Openblas the same,修复备忘
号外: $ clang-format -style"{BasedOnStyle: llvm, IndentWidth: 4}" -i hello.cpp $ clang-format -style"{BasedOnStyle: llvm, IndentWidth: 4}" -i hello.cpp IndentWidth:4不错,默认2太下了 1,现象 MN103040时&…...

[后端代码审计] PHP 数组知识汇总
文章目录 前言1. 数组基础1.1 数组概念1.2 索引数组1.3 关联数组1.4 多维数组 2. 数组函数2.1 count()2.2 array_merge()2.3 array_keys()2.4 array_values()2.5 in_array() 3. 数组遍历3.1 for循环遍历3.2 foreach遍历3.3 遍历索引数组3.4 遍历关联数组 4. 数组排序4.1 sort()…...

单点Redis中面临哪些问题
我的后端学习大纲 我的Redis学习大纲 1.面试:请说下在单点Redis中面临哪些问题: 1.1.单点Redis的问题: 1.数据丢失问题:Redis是内存存储,服务重启可能会丢失数据 2.并发能力问题:单节点Redis并发能力虽然…...

数学建模--蒙特卡洛算法之电子管更换刀片寿命问题
目录 1.电子管问题重述 2.电子管问题分析 3.电子管问题求解 4.刀片问题重述 5.刀片问题分析 6.刀片问题求解 1.电子管问题重述 某设备上安装有4只型号规格完全相同的电子管,已知电子管寿命服从100~200h之间的均匀分布. 只要有一个电子管…...

如何解码Linux下事件响应工具evtest的时间戳
evtest介绍 这里放一下原文链接evtest工具介绍及安装 在开发input子系统驱动时,常常会使用evtest工具进行测试。evtest是打印evdev内核事件的工具,它直接从内核设备读取并打印设备描述的带有值和符号名的事件,可以用来调试鼠标、键盘、触摸…...

基于STM32开发的智能门禁系统
目录 引言环境准备工作 硬件准备软件安装与配置系统设计 系统架构硬件连接代码实现 初始化代码控制代码应用场景 小区门禁管理企业办公门禁系统常见问题及解决方案 常见问题解决方案结论 1. 引言 智能门禁系统通过整合多种身份识别技术,如密码输入、RFID刷卡、指…...

EasyExcel-高性能的 Java Excel 处理库
EasyExcel 是阿里巴巴开发的一个高性能的 Java Excel 处理库,主要用于处理大规模的 Excel 文件。它特别注重性能,优化了内存消耗,适合处理大数据量的 Excel 文件,避免了传统 Excel 库在处理大文件时的性能瓶颈。 主要功能 高性能…...

精益生产培训秘籍:六步策略,助力企业降本增效——张驰咨询
在当今竞争激烈的市场环境中,企业为了提高生产效率、降低成本、增强市场竞争力,纷纷引入精益生产理念。精益生产作为一种以客户需求为导向,通过持续消除浪费、优化流程、提升质量的生产方式,已成为众多企业转型升级的利器。张驰咨…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
