leetcode50. Pow(x, n),快速幂算法
leetcode50. Pow(x, n),快速幂算法
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
目录
- leetcode50. Pow(x, n),快速幂算法
- 总体思维导图
- 快速幂算法详解
- 算法背景
- 算法原理
- 算法步骤
- 算法优势
- 应用场景
- 流程图
- 具体代码
- 算法分析
- 相似题目
总体思维导图

快速幂算法详解
算法背景
快速幂算法是一种高效计算 x n x^n xn 的方法,特别适用于 n n n 非常大的情况。它基于幂的性质和二进制表示。
算法原理
- 二进制表示:任何整数 n n n 都可以用二进制表示。例如, 13 13 13 的二进制表示是 1101 1101 1101。
- 幂的性质: x n x^n xn 可以分解为 x 2 0 × x 2 1 × x 2 2 × … x^{2^0} \times x^{2^1} \times x^{2^2} \times \ldots x20×x21×x22×… 的形式。例如, x 13 x^{13} x13 可以分解为 x 1 × x 4 × x 8 x^{1} \times x^{4} \times x^{8} x1×x4×x8。
- 位操作:通过检查 n n n 的二进制表示中的每一位,我们可以确定是否需要将对应的 x 2 k x^{2^k} x2k 乘入结果中。
算法步骤
-
初始化:
- 设置结果
res为 1。 - 将指数 n n n 转换为长整型
nn以避免在负数时的整数溢出。
- 设置结果
-
特殊情况处理:
- 如果 x = 1 x = 1 x=1,直接返回 x x x。
- 如果 x = − 1 x = -1 x=−1,根据 n n n 的奇偶性返回 x x x 或 − x -x −x。
- 如果 n < 0 n < 0 n<0,将 n n nn nn 设为正数,并将 x x x 设为其倒数。
-
快速幂计算:
- 使用 while 循环,当 n n > 0 nn > 0 nn>0 时执行。
- 如果 n n nn nn 的当前最低位为 1(
nn & 1),则将 r e s res res 乘以 x x x。 - 将 n n nn nn 右移一位(
nn >>= 1),即除以 2。 - 将 x x x 平方(
x = x * x)。
-
返回结果:
- 当 n n nn nn 变为 0 时,返回
res。
- 当 n n nn nn 变为 0 时,返回
算法优势
- 时间复杂度降低:传统的幂运算需要 O ( n ) O(n) O(n) 的时间复杂度,而快速幂算法只需要 O ( log n ) O(\log n) O(logn)。
- 减少乘法操作:通过跳过不必要的乘法,算法减少了计算量。
应用场景
快速幂算法常用于需要高效率幂运算的场合,例如密码学、大数运算等。
这个算法的关键在于利用了二进制的性质和位操作,从而将一个复杂的幂运算问题转化为一系列更简单的乘法和位移操作。
流程图
具体代码
class Solution {
public:double myPow(double x, int n) {double res=1;long long nn=(long long)n;if(x==1.00000){return x;}if(x==-1.00000){if(nn%2==1) return x;else return -x;}if(nn<0) {nn=-nn;x=1/x;}while(nn){if(nn&1) res*=x;nn>>=1;x=x*x;}return res;}
};
算法分析
- 时间复杂度: O ( log n ) O(\log n) O(logn),因为每次循环 n n n 都至少减少一半。
- 空间复杂度: O ( 1 ) O(1) O(1),只使用了常数空间。
- 易错点:处理负指数和 x = − 1 x = -1 x=−1 的情况时容易出错。
- 注意点:使用
long long类型处理大指数,防止整数溢出。
相似题目
下面是一些与快速幂算法相关的题目,您可能会感兴趣:
| 题目 | 链接 |
|---|---|
| Pow(x, n) | LeetCode |
| Super Pow | LeetCode |
| Pow(x, n) II | LintCode |
这些题目都可以使用快速幂算法来解决。
相关文章:

leetcode50. Pow(x, n),快速幂算法
leetcode50. Pow(x, n),快速幂算法 实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 示例 1: 输入:x 2.00000, n 10 输出:1024.00000 示例 2: 输入ÿ…...

Xinstall神器来袭,轻松搞定CPA推广渠道统计!
在数字化营销日益盛行的今天,CPA(按行动付费)推广已成为众多企业营销的重要手段。然而,随着渠道流量和获客途径的不断变化,CPA推广渠道统计的痛点也日益凸显。别担心,Xinstall来帮你解决问题! …...

011 | efinance分析豆一主连期货
👉👉👉 《玩转Python金融量化专栏》👈👈👈 订阅本专栏的可以下载对应的代码和数据集 🚀 上一篇🌟 下一篇⬅️ 010 东方财富帖子标题情绪分析012 akshare分析NYBOT棉花历史数据 ➡️豆一主连期货(通常简称“豆一”)是指中国期货市场上以大豆为标的的期货合约…...

【Python】函数入门(下)
3))* ** 注意:也遵循位置传参在前面,按关键字传参在后面。 代码示例: def func(*args,**kwargs):print(args,kwargs) 该函数中的参数会自动根据传参的方式不同(即:按位置…...

git的基本概念和使用原理
Git是一个分布式版本控制系统,用于跟踪文件的更改并协调多个开发人员之间的工作。以下是Git的基本概念和使用原理及方式: 目录 基本概念 使用原理 基本操作示例 基本概念 版本库(Repository): 版本库是Git用来保存…...

手写简化版的vue-router
vue-router作为vue全家桶之一的重要插件,有必要去深究一下,今天我们就从0到1手写一个简化版本。 开始之前,我们使用路由插件时是先进行下载路由 npm i vue-router ,然后在main.js中使用app.use导入router插件。想要手写vue-rou…...

分享一个基于uni-app的蛋糕商城订购小程序的设计与实现(源码、调试、LW、开题、PPT)
💕💕作者:计算机源码社 💕💕个人简介:本人 八年开发经验,擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等,大家有这一块的问题可以一起交流&…...

Python绘图入门:使用Matplotlib绘制柱状图
Python绘图入门:使用Matplotlib绘制柱状图 柱状图是一种常见的数据可视化方式,能够直观地展示不同类别之间的数据差异。在Python中,Matplotlib是一个非常强大且灵活的绘图库,它不仅能绘制简单的图表,还能创建复杂的多…...

Qt5编译qmqtt库使用MQTT协议连接华为云IOT完成数据上传与交互
一、前言 随着物联网技术的发展,越来越多的设备通过网络互相连接,形成了庞大的智能系统。这些系统能够收集、分析并响应各种数据,从而实现自动化控制和智能化管理。在这个背景下,MQTT 成为了一个广泛使用的轻量级消息传输协议,特别适用于资源受限的环境,如移动应用或远程…...

mysql速起架子
wget https://dev.mysql.com/get/Downloads/MySQL-8.0/mysql-8.0.21-linux-glibc2.12-x86_64.tar.xz 下载mysql tar xvJf mysql-8.0.21-linux-glibc2.12-x86_64.tar.xz 解压 mv mysql-8.0.21-linux-glibc2.12-x86_64 mysql-8.0 改名 去到bin目录 cd bin mkdir data gr…...

云动态摘要 2024-08-14
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 注册阿里云免费领云服务器_云服务器ECS_阿里云 阿里云 2024-08-14 云上试用新玩法,个人享300元免费额度,企业享660元免费额度,多种规格随心试 [免费体验…...
聚合详解及示例)
Elasticsearch 桶(Bucket)聚合详解及示例
在 Elasticsearch 中,桶(Bucket)聚合是一种强大的工具,它允许我们对数据进行分组并统计每组的数量。这种聚合类型对于理解数据的分布和进行分组统计非常有用。本文将详细介绍 Elasticsearch 的桶聚合,并提供完整的示例…...
Django基础知识
文章目录 新建Django项目helloworld关联数据库admin 新建Django项目 创建django-admin startproject project_name 运行 python manage.py runserver 创建app: python manage.py startapp app_name 目录: 配置文件 settings.py 路由配置 urls.py 项目管理 manage.p…...

使用 nginx 搭建代理服务器(正向代理 https 网站)指南
简介 正向代理 简介 在企业开发环境中,局域网内的设备通常需要通过正向代理服务器访问互联网。正向代理服务器充当中介,帮助客户端请求外部资源并返回结果。局域网内也就是俗称的内网,局域网外的互联网就是外网,在一些特殊场景内…...

深入解析亚马逊数据采集工具选择:Data API/Scrape API/Pangolin采集器
引言 在当今电商领域,亚马逊已成为全球最大的在线零售平台之一。随着竞争的加剧和市场的多样化,商家和企业不仅需要优秀的产品和服务,还需要通过深入的数据分析来制定更加精准的市场策略。因此,采集亚马逊站点数据已成为企业实现…...

探索Linux多样性:主流发行版及其应用场景
目录 引言 Debian:稳定性的标杆 Ubuntu:易用性的代表 Red Hat Enterprise Linux (RHEL):企业的首选 Fedora:创新的前沿 CentOS:开源的稳定之选 Arch Linux:高级用户的定制天堂 Gentoo:性…...

CentOS7.6 HAproxy-7层负载均衡集群——实施方案
目录 1、前期环境准备 1.准备4台主机 1. 设置主机名 2. 设置IP地址然后重启网卡 3. 关闭防火墙和selinux 4. 全部的服务器完成时间统一 二、配置haproxy(192.168.200.11)服务器 1. 安装haproxy 2. haproxy 配置中分成五部分内容 3. 配置HAproxy(192.168.2…...

升级ubuntu22.10到24.04
将所有kinetic换成noble,noble是24.04源,sed或手动改。 cd /etc/aptgrep -nr kinetic将old-releases.ubuntu.com替换成国内的地址,因为2210国内源没找到,没有了,但是现在更新到24.04,国内是有的。 apt up…...
YOLO好像也没那么难?
“学YOLO的念头是想整个游戏外挂!” 目录 基本原理 模型推理 IOU交并比 NMS非极大值抑制 模型训练 损失函数LOSS 代码实现 YOLO学习渠道 基本原理 模型推理 学习一个新的神经网络结构,作者认为整明白输入和输出是怎么回事就OK了,至于…...
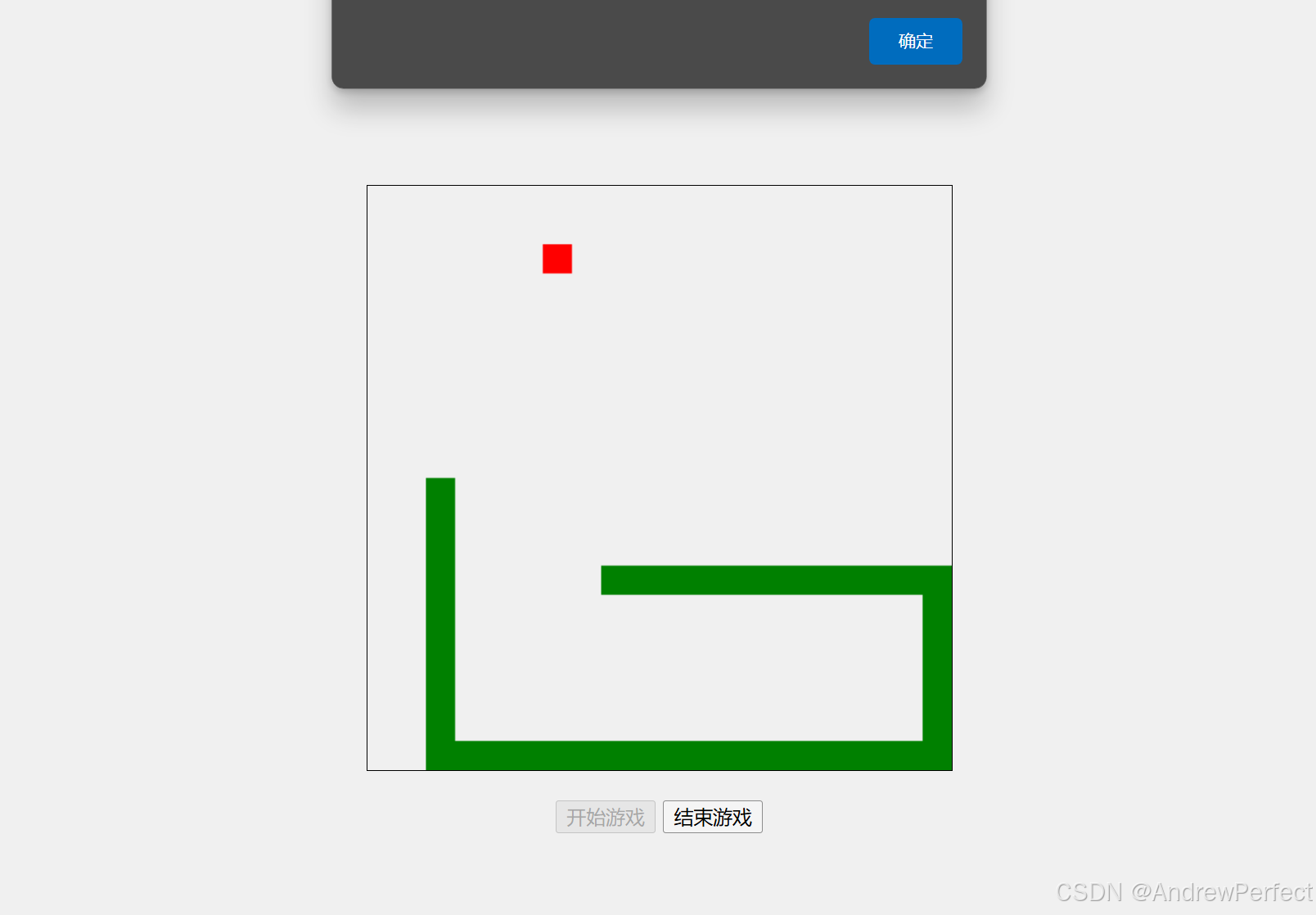
html编写贪吃蛇页面小游戏(可以玩)
<!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>贪吃蛇小游戏</title><style>body {…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
