【C++】多源BFS问题和拓扑排序
目录
多源BFS介绍
单源BFS和多源BFS的区别
SO如何解决多源BFS问题
多源之核心
矩阵
算法思路
代码实现
飞地的数量
算法思路
代码实现
地图中的最高点
算法思路
代码实现
地图分析
算法思路
代码实现
拓扑排序介绍
有向无环图
编辑
如何解决这类问题
课程表
算法思路
代码实现
课程表2
算法思路
代码实现
火星词典
代码实现
多源BFS介绍
单源BFS和多源BFS的区别
顾名思义,单源BFS是只有一个起点,博客CSDN中已经阐述过,如有不明白者,可前去一探究竟,而多源BFS是有多个起点,然后同时出发,到达终点;
SO如何解决多源BFS问题
多源的BFS,本质上与单源的BFS并无太大差别,我们只需要把多个起点等效成一个起点即可,这样就转化为了单源的问题了。
多源之核心
将所有的起点都加入队列---->扩散----->终点。与单源之秘法极其类似,方能解之。
矩阵
例题地址. - 力扣(LeetCode)
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:mat = [[0,0,0],[0,1,0],[0,0,0]] 输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
输入:mat = [[0,0,0],[0,1,0],[1,1,1]] 输出:[[0,0,0],[0,1,0],[1,2,1]]
算法思路
代码实现
class Solution {
public:int m,n;int dx[4]={1,-1,0,0};int dy[4]={0,0,1,-1};vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {m=mat.size();n=mat[0].size();vector<vector<int>>ans(m,vector<int>(n,-1));queue<pair<int,int>>q;//储存所有的原点for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(mat[i][j]==0){q.push({i,j});ans[i][j]=0;}}}int ret=0;while(q.size()){ret++;int sz=q.size();while(sz--){auto [a,b]=q.front();q.pop();for(int i=0;i<4;i++){int x=a+dx[i];int y=b+dy[i];if(x>=0&&x<m&&y>=0&&y<n&&ans[x][y]==-1){ans[x][y]=ret;q.push({x,y});}}}}return ans;}
};飞地的数量
例题地址:. - 力扣(LeetCode)
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
示例 1:
输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] 输出:3 解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
示例 2:
输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] 输出:0 解释:所有 1 都在边界上或可以到达边界。
算法思路

代码实现
class Solution {
public:int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};int numEnclaves(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();bool vis[m][n];memset(vis,0,sizeof vis);queue<pair<int,int>>q;//储存原点for(int i=0;i<m;i++){for(int j=0;j<n;j++){if((i==0||i==m-1||j==0||j==n-1)){if(grid[i][j]==1){q.push({i,j});vis[i][j]=true;}}}}while(q.size()){auto [a,b]=q.front();q.pop();for(int i=0;i<4;i++){int x=a+dx[i];int y=b+dy[i];if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&!vis[x][y]){q.push({x,y});vis[x][y]=true;} }}int ret=0;for(int i=0;i<m;i++)for(int j=0;j<n;j++)if(grid[i][j]==1&&!vis[i][j])ret++;return ret;}
};地图中的最高点
地址:. - 力扣(LeetCode)
给你一个大小为 m x n 的整数矩阵 isWater ,它代表了一个由 陆地 和 水域 单元格组成的地图。
- 如果
isWater[i][j] == 0,格子(i, j)是一个 陆地 格子。 - 如果
isWater[i][j] == 1,格子(i, j)是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度:
- 每个格子的高度都必须是非负的。
- 如果一个格子是 水域 ,那么它的高度必须为
0。 - 任意相邻的格子高度差 至多 为
1。当两个格子在正东、南、西、北方向上相互紧挨着,就称它们为相邻的格子。(也就是说它们有一条公共边)
找到一种安排高度的方案,使得矩阵中的最高高度值 最大 。
请你返回一个大小为 m x n 的整数矩阵 height ,其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法,请返回 任意一个 。
示例 1:
输入:isWater = [[0,1],[0,0]] 输出:[[1,0],[2,1]] 解释:上图展示了给各个格子安排的高度。 蓝色格子是水域格,绿色格子是陆地格。
示例 2:
输入:isWater = [[0,0,1],[1,0,0],[0,0,0]] 输出:[[1,1,0],[0,1,1],[1,2,2]] 解释:所有安排方案中,最高可行高度为 2 。 任意安排方案中,只要最高高度为 2 且符合上述规则的,都为可行方案
算法思路

代码实现
class Solution {
public:int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};int numEnclaves(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();bool vis[m][n];memset(vis,0,sizeof vis);queue<pair<int,int>>q;//储存原点for(int i=0;i<m;i++){for(int j=0;j<n;j++){if((i==0||i==m-1||j==0||j==n-1)){if(grid[i][j]==1){q.push({i,j});vis[i][j]=true;}}}}while(q.size()){auto [a,b]=q.front();q.pop();for(int i=0;i<4;i++){int x=a+dx[i];int y=b+dy[i];if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1&&!vis[x][y]){q.push({x,y});vis[x][y]=true;} }}int ret=0;for(int i=0;i<m;i++)for(int j=0;j<n;j++)if(grid[i][j]==1&&!vis[i][j])ret++;return ret;}
};地图分析
地址:. - 力扣(LeetCode)
你现在手里有一份大小为 n x n 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 -1。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
示例 1:
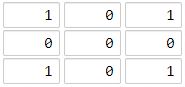
输入:grid = [[1,0,1],[0,0,0],[1,0,1]] 输出:2 解释: 海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大,最大距离为 2。
示例 2:
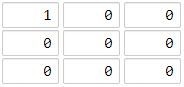
输入:grid = [[1,0,0],[0,0,0],[0,0,0]] 输出:4 解释: 海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大,最大距离为 4。
算法思路

代码实现
class Solution {
public:int dx[4]={1,-1,0,0};int dy[4]={0,0,1,-1};int maxDistance(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();vector<vector<bool>>vis(m,vector<bool>(n));//标记数组//将所有的1作为起点queue<pair<int,int>>q;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1){q.push({i,j});}}}int ret=0;if(q.size()==n*n||q.size()==0)retur n -1;while(q.size()){ret++;int sz=q.size();while(sz--){auto [a,b]=q.front();q.pop();for(int i=0;i<4;i++){int x=a+dx[i];int y=b+dy[i];if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==0&&!vis[x][y]){q.push({x,y});vis[x][y]=true;}}}}return ret-1;}
};拓扑排序介绍
有向无环图
入度:指向活动节点的箭头个数;
出度:从活动节点出去指向别的节点的箭头个数。
通过入度和出入我们可以判断活动的进行顺序,活动度数为0的活动先进行没进行完后,将该活动的出度清空,下一个入度为0的节点就是该节点之后要进行的活动,以此类推,直到最后没有活动节点,如果只存在有一个入度的节点(成环)。
如何解决这类问题
1.首先建图,也就是邻接矩阵,可以使用哈希表处理。
2.统计所有活动节点的出度和入度。
3.如果入度是0就把活动节点加入到队列中。
4.BFS每走一步就把该节点的出度清空,将下一个入度为0的节点加入队列中。
5.判断是否有环:遍历度数表,如果还存在度数不为0的活动节点,那么说明还有活动成环了;
课程表
地址:. - 力扣(LeetCode)
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其 中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]] 输出:true 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]] 输出:false 解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
算法思路

代码实现
class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {//首先构造邻接矩阵,也就是边int n=numCourses;unordered_map<int,vector<int>>edge;//储存每一个节点的入度//先把所有的节点放在了数组中vector<int>in(n);//后面要统计所有课程的度数是否为零//储存所有的边for(auto &x:prerequisites){int a=x[0];//最红的课程(终点)int b=x[1];//先学的课程(起点)//存进数组中edge[b].push_back(a);in[a]++;//对应节点的入度增加}//开始使用队列来处理无度数的节点queue<int>q;for(int i=0;i<n;i++)if(in[i]==0)q.push(i);//如果入度为零,就加入到队列while(q.size()){//取出无度数的节点auto tmp=q.front();q.pop();//然后取消所有与他有关的边for(auto& x: edge[tmp]){in[x]--;//是否要加入后面的课程if(in[x]==0)//如果没有度数了{q.push(x);}}}//判断是否有环for(auto i:in){if(i)//如果存在度数不为0的节点return false;}return true;}
};课程表2
地址:. - 力扣(LeetCode)
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]] 输出:[0,2,1,3] 解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。 因此,一个正确的课程顺序是[0,1,2,3]。另一个正确的排序是[0,2,1,3]
示例 3:
输入:numCourses = 1, prerequisites = [] 输出:[0]
算法思路
与上一道题一样。
代码实现
class Solution {
public:vector<int> findOrder(int n, vector<vector<int>>& p) {unordered_map<int,vector<int>>edge;//储存所有的节点vector<int>in(n);//统计所有节点的度数//建图for(auto &e:p){int a=e[0];//终点int b=e[1];//起点edge[b].push_back(a);in[a]++;//终点的入度数增加}//DFSqueue<int>q;for(int i=0;i<n;i++)if(in[i]==0)q.push(i);//储存所有的入度为零的节点.//储存结果的数组vector<int>ret;while(q.size()){auto t=q.front();q.pop();ret.push_back(t);for(auto x:edge[t])//遍历节点后的链接的节点{in[x]--;if(in[x]==0){q.push(x);}}}//判断是否有环for(auto x:in)if(x)return {};return ret;}
};火星词典
地址:. - 力扣(LeetCode)
现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。
给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。
请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序 排列。若不存在合法字母顺序,返回 "" 。若存在多种可能的合法字母顺序,返回其中 任意一种 顺序即可。
字符串 s 字典顺序小于 字符串 t 有两种情况:
- 在第一个不同字母处,如果
s中的字母在这门外星语言的字母顺序中位于t中字母之前,那么s的字典顺序小于t。 - 如果前面
min(s.length, t.length)字母都相同,那么s.length < t.length时,s的字典顺序也小于t。
示例 1:
输入:words = ["wrt","wrf","er","ett","rftt"] 输出:"wertf"
示例 2:
输入:words = ["z","x"] 输出:"zx"
示例 3:
输入:words = ["z","x","z"]
输出:""
解释:不存在合法字母顺序,因此返回 "" 。
代码实现
class Solution {
public:unordered_map<char,unordered_set<char>>edge;unordered_map<char,int>in;string alienOrder(vector<string>& words) {for(auto &str:words){for(auto x:str){in[x]=0;}}int n=words.size();for(int i=0;i<n;i++)for(int j=i+1;j<n;j++){bool tmp=add(words[i],words[j]);if(tmp==true)return "";}queue<char>q;for(auto [a,b]:in){if(b==0)q.push(a);}string ret;while(q.size()){auto t=q.front();q.pop();ret+=t;for(auto x:edge[t]){if(--in[x]==0)q.push(x);}}for(auto [a,b]:in)if(b)return "";return ret;}bool add(string & s1,string&s2){int n=min(s1.size(),s2.size());int i=0;for(;i<n;i++){if(s1[i]!=s2[i]){char a=s1[i];char b=s2[i];if(!edge.count(a)||!edge[a].count(b)){edge[a].insert(b);in[b]++;}break;}}if(i==s2.size()&&i<s1.size())return true; return false;}
};
相关文章:

【C++】多源BFS问题和拓扑排序
目录 多源BFS介绍 单源BFS和多源BFS的区别 SO如何解决多源BFS问题 多源之核心 矩阵 算法思路 代码实现 飞地的数量 算法思路 代码实现 地图中的最高点 算法思路 代码实现 地图分析 算法思路 代码实现 拓扑排序介绍 有向无环图 编辑 如何解决这类问题 课…...

CentOS 7 安装详细教程
大家好,我是程序员小羊! 前言: CentOS 7 是一个稳定的企业级 Linux 发行版,广泛用于服务器环境。CentOS 7 是基于 Red Hat Enterprise Linux (RHEL) 构建的企业级 Linux 发行版,提供免费的、开源的操作系统…...

mybatis-plus + springboot 多对多实例
在MyBatis Plus中,自动填充数据是一种非常实用的功能,它可以自动地为一些字段设置默认值,比如创建时间和更新时间。对于多对多关系来说,虽然自动填充主要针对单一实体的字段,但在某些情况下,你可能也需要在…...

SpringBoot日志整合
Spring Boot 整合日志框架的核心是通过 spring-boot-starter-logging 依赖来实现的,它默认整合了 Logback 日志框架。 Spring Boot 对各种日志框架进行了自动配置,使得我们可以很容易地在 Spring Boot 应用中使用日志。 Spring Boot 在类路径下寻找 Log…...
信创教育:培养未来科技创新的生力军
随着全球数字化转型的加速,信息技术应用创新(简称“信创”)产业作为推动国家信息技术自主可控和产业升级的关键领域,正迎来前所未有的发展机遇。信创教育,作为培养未来科技创新生力军的重要阵地,其重要性和…...

slowfast
核心网络网络架构: 1、分别获取高频和低频图像数据 2、分别进行特征提取 3、特征融合 4、预测 网络结构细节:...
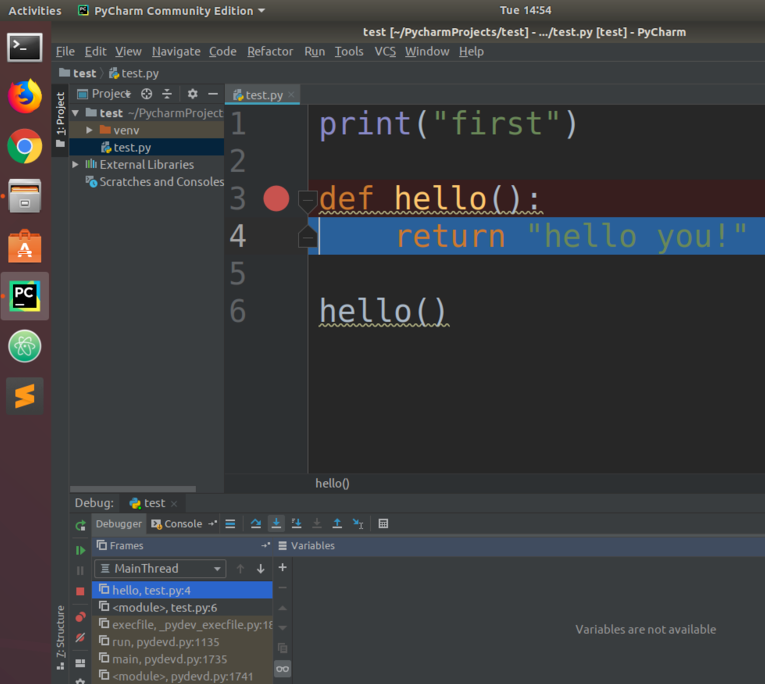
怎么调试python脚本
打开pycharm community 2019.1软件,创建一个项目。 创建一个py后缀的文件作为示范,文件名自己定义。 编写代码,然后右键点击进行运行,查看一下是否有问题。 点击右上角的虫子图标,然后下面会有控制面板出来,…...

Flask获取请求信息
示例代码 from flask import Flaskapp = Flask(__name__)if __name__ == "__main__": app.run(debug=True) 1、获取请求头 from flask import request@app.route("/headers", methods=["GET"])def get_headers(): headers = request.heade…...

Overleaf中放置高分辨率图片的方法
如果将ppt中的图片另存为png或jpg等格式,如果图中有密集的编码网格,则生成的pdf会糊掉。如何确保生成的pdf中的图片放大后仍然保持细节?亲测方案: 1、将ppt中的图片尺寸记下来,然后在ppt→设计中将ppt模板的大小设置成…...

【C语言】动态内存管理(malloc,free,calloc,realloc详解 )
🦄个人主页:小米里的大麦-CSDN博客 🎏所属专栏:https://blog.csdn.net/huangcancan666/category_12718530.html 🎁代码托管:C语言: C语言方向(基础知识和应用) (gitee.com) ⚙️操作环境:Visual Studio 2022 目录 一、…...

如何寻找数值仿真参数最优解?CFD参数优化详解3来袭
本期文章将通过2个简单案例演示参数优化的操作步骤,一起来看看吧! 流程自动化 实现 CFD 参数优化,首先要创建流程自动化。用户可采用SimLab的Python宏命令,录制建模流程。或在HyperWorks CFD模块的Template Manager创建Tcl/Tk命令…...

虚拟机macos中构建llvm、clang并配置Xcode
安装虚拟机macos,并安装brew: 安装vmware:https://www.bilibili.com/video/BV1Wo4y1E7fc/安装最新版的macos:极限苹果-Mac论坛-提供Mac软件和macOS苹果系统镜像下载下载并安装brew:版本要低,我装的是4.3.5…...

Java 中的 @SneakyThrows 注解详解:简化异常处理的利与弊
在 Java 开发中,异常处理是一个不可避免的重要部分。我们经常需要处理各种检查型异常(checked exceptions),这有时会导致代码变得冗长且难以维护。为了简化异常处理,Lombok 提供了一个强大的注解——SneakyThrows。本文…...

系统编程 day11 进程(线程)3
fork函数的总结: 总结对进程学习之中的回收函数wait wait函数: 1.获取子进程的退出状态 2.回收资源------会让僵尸态的子进程销毁 注:1.wait函数本身是一个阻塞操作,会使调用者阻塞 2.父进程要获得子进程的退出状态 子进程&…...

[ Python 原理分析 ]如何实现用户实现博客文章点赞-物联网Python
目录 一、前言 二、Python爬虫 三、详细操作 3.1 建立基本工程 3.2 获取文章列表 3.2.1 找到获取文章请求 3.2.2 分析获取请求 3.2.3 构建获取请求 3.2.4 调试打印 3.3 实现点赞操作 3.3.1 判断点赞状态 3.3.2 找到点赞请求 3.2.3 分析点赞请求 3.2.4 构建点赞请…...

【47 Pandas+Pyecharts | 杭州二手房数据分析可视化】
文章目录 🏳️🌈 1. 导入模块🏳️🌈 2. Pandas数据处理2.1 读取数据2.2 过滤数据2.3 行政区处理2.4 地址处理2.5 房屋信息处理2.6 面积处理2.7 楼层处理2.8 年份处理2.9 房价处理2.10 删除不用的列2.11 数据类型转换2.12 查看…...

C++入门基础知识13
C 的关键字(接上一篇博文)!! 10. const_cast用法: 该运算符用来修改类型的 const 或 volatile 属性。除了 const 或 volatile 修饰之外, type_id 和 expression 的类型是一样的。常量指针被转化成非常量指针…...

IP地址证如何实现HTTPS访问?(内网IP、公网IP)
IP地址证书(全称为IP地址的SSL/TLS证书)是实现通过IP地址进行HTTPS访问的关键。以下是实现这一目标的详细步骤: 一、选择证书颁发机构(CA) 1.选择支持IP证书的CA:并非所有证书颁发机构都提供为IP地址颁…...

东土科技车规级网络芯片获批量应用
东土科技孵化的我国第一颗国产汽车芯片名录的车规级TSN交换网络芯片,于近期获得国家新能源汽车技术创新中心10万片芯片订单,将规模化应用于车载网关,赋能新一代自主可控汽车网络通信架构。 车规级TSN交换网络芯片于2021年流片成功࿰…...

nvidia系列教程-AGX-Orin pcie扩展M.2磁盘调试笔记
目录 前言 一、AGX-Orin pcie接口介绍 二、原理图连接 三、SDK配置 四、M.2磁盘调试 总结 前言 NVIDIA Jetson AGX Orin 是一款强大的嵌入式平台,广泛应用于 AI 推理、机器人和自动驾驶等领域。在扩展存储方面,PCIe 接口的 M.2 SSD 是一个常见的选择。本篇博客将记录如何…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...


