letcode 分类练习 树的遍历
letcode 分类练习 树的遍历
- 树的构建
- 递归遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 迭代遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 层序遍历可以解决的问题
- 107. 二叉树的层序遍历 II
- 199. 二叉树的右视图
- 637. 二叉树的层平均值
- 429. N 叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针II
- 104.二叉树的最大深度
- 111.二叉树的最小深度
树的构建
输入数组:[8, 3, 10, 1, 6, null, 14, null, null, 4, 7, 13]

#include <iostream>
#include <vector>
#include <queue>
#include <memory>using namespace std;// 定义二叉树节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 根据向量数组构建二叉树
TreeNode* constructBinaryTree(const vector<int*>& nums) {if (nums.empty() || !nums[0]) {return nullptr;}// 使用队列进行层序遍历构建树queue<TreeNode*> q;TreeNode* root = new TreeNode(*nums[0]);q.push(root);int i = 1;while (!q.empty() && i < nums.size()) {TreeNode* current = q.front();q.pop();// 构建左子节点if (i < nums.size() && nums[i]) {current->left = new TreeNode(*nums[i]);q.push(current->left);}i++;// 构建右子节点if (i < nums.size() && nums[i]) {current->right = new TreeNode(*nums[i]);q.push(current->right);}i++;}return root;
}
递归遍历
前序遍历
class Solution {
public:vector<int> result;void dfs(TreeNode* root){if(!root) return;result.push_back(root->val);if(root -> left)dfs(root -> left);if(root -> right)dfs(root-> right);}vector<int> preorderTraversal(TreeNode* root) {dfs(root);return result;}
};
中序遍历
class Solution {
public:vector<int> result;void dfs(TreeNode* root){if(!root) return;if(root->left)dfs(root->left);result.push_back(root -> val);if(root->right)dfs(root->right);}vector<int> inorderTraversal(TreeNode* root) {dfs(root);return result;}
};
后序遍历
class Solution {
public:vector<int> result;void dfs(TreeNode* root){if(!root) return;if(root->left)dfs(root->left);if(root->right)dfs(root->right);result.push_back(root -> val);}vector<int> postorderTraversal(TreeNode* root) {dfs(root);return result;}
};
迭代遍历
前序遍历

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> result;if(!root)return result;while(root || !s.empty()){while(root){s.push(root);// 这里while一直向左就开始收集result.push_back(root->val);root = root -> left;}TreeNode* node = s.top();s.pop();root = node -> right;}return result;}
};
中序遍历

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> result;if(!root)return result;while(root || !s.empty()){while(root){s.push(root);root = root -> left;}TreeNode* node = s.top();s.pop();// 弹栈的时候才收集result.push_back(node->val);root = node -> right;}return result;}
};
后序遍历

后序遍历的迭代方式有区别,就是弹栈后,不是收集,而是判断它的右孩子节点,如果右孩子为空,说明它是叶子节点,这个时候我们收集到result里,并且把这个标记成前驱节点,root再置为空。如果右孩子不为空,我们要像访问左孩子这样继续遍历。
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> s;vector<int> result;if(!root) return result;TreeNode* prev;while(root || !s.empty()){while(root){s.push(root);root = root -> left;}TreeNode* root = s.top();s.pop();if(root -> right == nullptr && root != prev){result.push_back(root -> val);prev = root;root = root -> right;}else{s.push(root);root = root -> right;}}return result;}
};
层序遍历

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*>q;vector<vector<int>> result;if(!root)return result;q.push(root);while(!q.empty()){int k = q.size();vector<int> tmp;for(int i =0;i<k;i++){TreeNode* node = q.front();q.pop();tmp.push_back(node -> val);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}result.push_back(tmp);}return result;}
};
层序遍历可以解决的问题
107. 二叉树的层序遍历 II

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*>q;vector<vector<int>> result;if(!root)return result;q.push(root);while(!q.empty()){int k = q.size();vector<int> tmp;for(int i =0;i<k;i++){TreeNode* node = q.front();q.pop();tmp.push_back(node -> val);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}result.push_back(tmp);}reverse(result.begin(), result.end());return result;}
};
199. 二叉树的右视图

class Solution {
public:vector<int> rightSideView(TreeNode* root) {queue<TreeNode*>q;vector<int> result;if(!root)return result;q.push(root);while(!q.empty()){int k = q.size();vector<int> tmp;for(int i =0;i<k;i++){TreeNode* node = q.front();q.pop();if(i==k-1) result.push_back(node -> val);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}}return result;}
};
637. 二叉树的层平均值

class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {queue<TreeNode*>q;vector<double> result;if(!root)return result;q.push(root);while(!q.empty()){int k = q.size();vector<int> tmp;double sum = 0;for(int i =0;i<k;i++){TreeNode* node = q.front();sum += node->val;q.pop();if(i==k-1) result.push_back(sum/k);if(node->left)q.push(node->left);if(node->right)q.push(node->right);}}return result;}
};
429. N 叉树的层序遍历

class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*> q;vector<vector<int>>result;if(!root)return result;q.push(root);while(!q.empty()){int k = q.size();vector<int>tmp;for(int i =0;i<k;i++){Node* node = q.front();q.pop();tmp.push_back(node->val);for(auto c : node->children){q.push(c);}}result.push_back(tmp);}return result;}
};
515.在每个树行中找最大值

class Solution {
public:vector<int> largestValues(TreeNode* root) {queue<TreeNode*> q;vector<int> result;if(!root) return result;q.push(root);while(!q.empty()){int k = q.size();int maxV = INT_MIN;for(int i =0;i<k;i++){TreeNode* node = q.front();q.pop();if(node -> val > maxV)maxV = node -> val;if(i == k-1)result.push_back(maxV);if(node -> left)q.push(node -> left);if(node -> right)q.push(node -> right);}}return result;}
};
116.填充每个节点的下一个右侧节点指针

class Solution {
public:Node* connect(Node* root) {queue<Node*> q;if(!root) return root;q.push(root);while(!q.empty()){int k = q.size();Node* tmp = NULL;for(int i =0;i<k;i++){Node* node = q.front();q.pop();if(tmp != NULL)tmp -> next = node;tmp = node;if(node -> left)q.push(node -> left);if(node -> right)q.push(node -> right);}}return root;}
};
117.填充每个节点的下一个右侧节点指针II

class Solution {
public:Node* connect(Node* root) {queue<Node*> q;if(!root) return root;q.push(root);while(!q.empty()){int k = q.size();Node* tmp = NULL;for(int i =0;i<k;i++){Node* node = q.front();q.pop();if(tmp != NULL)tmp -> next = node;tmp = node;if(node -> left)q.push(node -> left);if(node -> right)q.push(node -> right);}}return root;}
};
104.二叉树的最大深度

class Solution {
public:int maxDepth(TreeNode* root) {queue<TreeNode*> q;if(!root) return 0;q.push(root);int count = 0;while(!q.empty()){int k = q.size();count++;for(int i =0;i<k;i++){TreeNode* node = q.front();q.pop();if(node -> left)q.push(node -> left);if(node -> right)q.push(node -> right);}}return count;}
};
111.二叉树的最小深度
 如果是叶子节点提前返回
如果是叶子节点提前返回
class Solution {
public:int minDepth(TreeNode* root) {queue<TreeNode*> q;if(!root) return 0;q.push(root);int count = 0;while(!q.empty()){int k = q.size();count++;for(int i =0;i<k;i++){TreeNode* node = q.front();q.pop();if(!node -> left && !node -> right)return count;if(node -> left)q.push(node -> left);if(node -> right)q.push(node -> right);}}return count;}
};
相关文章:

letcode 分类练习 树的遍历
letcode 分类练习 树的遍历 树的构建递归遍历前序遍历中序遍历后序遍历 迭代遍历前序遍历中序遍历后序遍历 层序遍历层序遍历可以解决的问题107. 二叉树的层序遍历 II199. 二叉树的右视图637. 二叉树的层平均值429. N 叉树的层序遍历515.在每个树行中找最大值116.填充每个节点的…...

redisssion分布式锁
分布式锁的问题 基于setnx的分布式锁实现起来并不复杂,不过却存在一些问题。 锁误删问题 第一个问题就是锁误删问题,目前释放锁的操作是基于DEL,但是在极端情况下会出现问题。 例如,有线程1获取锁成功,并且执行完任…...

嘎嘎嘎拿到去年想要的包
一年多了 继续,把项目收尾吧 好好学前端,外企!react!从0开始,紧迫!加油!...
前奏编曲:如何编写二段式前奏
选好音源 Pianoteq 6 STAGE比较明亮些,适合做前奏的音源 确定和弦进行 比如4536251,每个小节2和弦,每个小节的和弦弹一下 优化和弦进行衔接和织体 二段式不用对和弦进行就近解决的处理,因为前奏前后要形成对比。 前半部分往…...

征服云端:Kubernetes如何让微服务与云原生技术如虎添翼
引言 在这个数字化转型的时代,微服务架构已经成为构建现代应用程序的首选方式。它不仅提高了开发效率,还增强了系统的可扩展性和灵活性。而随着云计算技术的迅猛发展,云原生的概念逐渐深入人心,它代表了一种全新的软件开发方法论…...

开源AI智能名片系统与高级机器学习技术的融合应用:重塑商务交流的未来
摘要:在数字化浪潮的推动下,人工智能(AI)技术,尤其是机器学习领域的快速发展,正深刻改变着各行各业的面貌。开源AI智能名片系统作为这一变革的先锋,通过集成并优化多种高级机器学习技术…...

Java中synchronized的偏向锁是如何减少锁开销的
偏向锁(Biased Locking)是一种优化 Java synchronized 锁的机制,旨在减少在无竞争情况下的锁开销。它通过将锁偏向于单个线程来优化锁的性能。以下是偏向锁减少锁开销的具体方式和原理: 偏向锁的工作原理 锁的初始状态: 当一个对…...

react18 + ts 使用video.js 直播.m3u8格式的视频流
一、安装依赖 我使用的video.js版本是8.17.3,从 Video.js 7.x 开始,HLS 支持被内置到了 Video.js 中所以不需要安装其他依赖 npm i video.js 二、创建VideoPlayer组件 import React, { useEffect, useRef } from react import videojs from video.js …...

使用 onBeforeRouteLeave 组合式函数提升应用的用户体验
title: 使用 onBeforeRouteLeave 组合式函数提升应用的用户体验 date: 2024/8/14 updated: 2024/8/14 author: cmdragon excerpt: 摘要:本文介绍了在Nuxtjs中使用onBeforeRouteLeave组合式函数来提升应用用户体验的方法。onBeforeRouteLeave允许在组件离开当前路…...

uni-app 吸顶方案总结
效果 页面级 uni.pageScrollTo 官方文档:https://uniapp.dcloud.net.cn/api/ui/scroll.html#pagescrollto 原生头部导航 uni.pageScrollTo({selector: #tabs,duration: 300 });(推荐)需要兼容自定义头部导航 <template><view id"demo1" :styl…...

【C#】知识汇总
目录 1 概述1.1 GC(Garbage Collection)1.1.1 为什么需要GC?1.1.2 GC的工作原理工作原理什么是Root?GC算法:Mark-Compact 标记压缩算法GC优化:Generational 分代算法 1.1.3 GC的触发时间1.1.4 如何减少垃圾…...

1、Unity【基础】3D数学
3D数学 文章目录 3D数学1、数学计算公共类Mathf1、Mathf和Math2、区别3、Mathf中的常用方法(一般计算一次)4、Mathf中的常用方法(一般不停计算)练习 A物体跟随B物体移动 2、三角函数1、角度和弧度2、三角函数3、反三角函数练习 物…...

虚拟机ubuntu22的扩容记录
这里lsblk命令能看到, ubuntu逻辑分区只有29G, 但总分区60G,还有接近30G未使用。 rootx:/home/x# lsblk NAME MAJ:MIN RM SIZE RO TYPE MOUNTPOINTS loop0 7:0 0 63.9M 1 loop /snap/core2…...

Docker 常用配置
Docker 常用配置 1. 配置方法 修改下面位置: Linux:vim /etc/docker/daemon.jsonmacOS:菜单栏图标->Settings->Docker Engine 注意:修改完需要重启Docker Linux:systemctl restart dockermacOS:…...

通过示例了解 .NET Core 中的依赖注入
依赖注入 (DI) 是一种用于实现 IoC(控制反转)的设计模式,可以更好地解耦应用程序内的依赖关系并更轻松地管理它们。.NET Core 内置了对依赖注入的支持,提供了一种有效管理依赖关系的强大方法。 一.什么是依赖注入? 依…...

fetch、FormData上传多张图片
利用fetch方法和FormData对象上传多张图片 formdata()对象可以序列化多张图片 <html><head><meta http-equiv"content-type" content"text/html;charsetUTF-8"/><title>测试fetch和formdata上传多张图片</title></head&…...

C++STL详解(五)——list类的具体实现
一.本次所需实现的三个类及其成员函数接口 链表首先要有结点,因此我们需要实现一个结点类。 链表要有管理结点的结构,因此我们要有list类来管理结点。 链表中还要有迭代器,而迭代器的底层其实是指针。但是我们现有的结点类无法完成迭代器的…...

鸿蒙(API 12 Beta3版)【使用投播组件】案例应用
华为视频接入播控中心和投播能力概述** 华为视频在进入影片详情页播放时,支持在控制中心查看当前播放的视频信息,并进行快进、快退、拖动进度、播放暂停、下一集、调节音量等操作,方便用户通过控制中心来操作当前播放的视频。 当用户希望通…...

【STM32项目】在FreeRtos背景下的实战项目的实现过程(一)
个人主页~ 这篇文章是我亲身经历的,在做完一个项目之后总结的经验,虽然我没有将整个项目给放出来,因为这项目确实也是花了米让导师指导的,但是这个过程对于STM32的实战项目开发都是非常好用的,可以说按照这个过程&…...

C#垃圾处理机制相关笔记
C#编程中的垃圾处理机制主要通过垃圾回收器(Garbage Collector,GC)实现自动内存管理。C#作为一种托管语言,其垃圾处理机制显著减轻了程序员的内存管理负担,与C语言等非托管语言形成鲜明对比。具体介绍如下:…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...
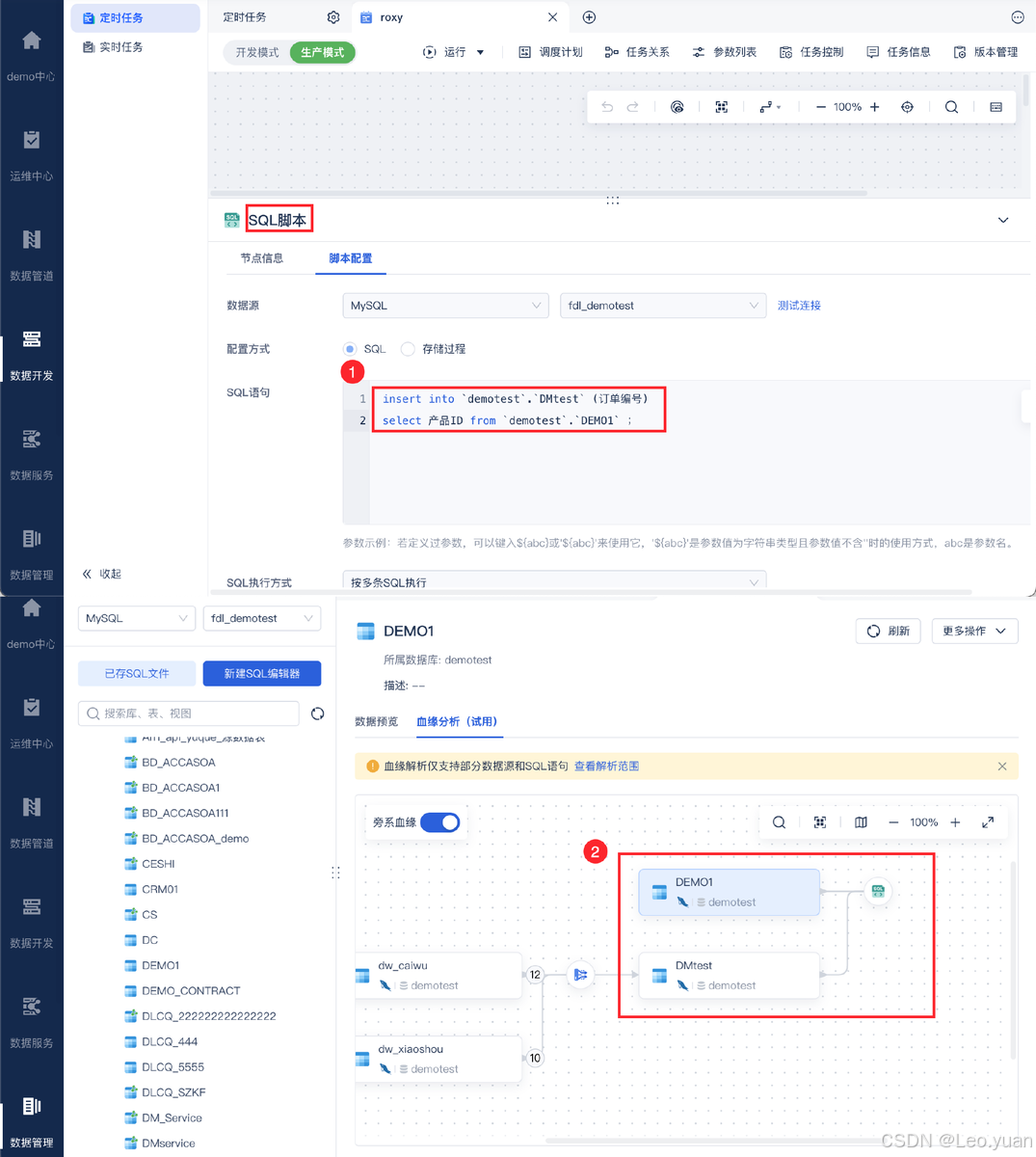
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...

CppCon 2015 学习:Simple, Extensible Pattern Matching in C++14
什么是 Pattern Matching(模式匹配) ❝ 模式匹配就是一种“描述式”的写法,不需要你手动判断、提取数据,而是直接描述你希望的数据结构是什么样子,系统自动判断并提取。❞ 你给的定义拆解: ✴ Instead of …...

ABB馈线保护 REJ601 BD446NN1XG
配电网基本量程数字继电器 REJ601是一种专用馈线保护继电器,用于保护一次和二次配电网络中的公用事业和工业电力系统。该继电器在一个单元中提供了保护和监控功能的优化组合,具有同类产品中最佳的性能和可用性。 REJ601是一种专用馈线保护继电器…...
