ccfcsp-202309(1、2、3)
202309-1 坐标变换(其一)
#include <bits/stdc++.h>
using namespace std;
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n, m;cin >> n >> m;int x, y;int opx = 0, opy = 0;for(int i = 0; i < n; i++){cin >> x >> y;opx += x;opy += y;}for(int i = 0; i < m; i++){cin >> x >> y;cout << x + opx << " " << y + opy << endl;}return 0;
}
202309-2 坐标变换(其二)
80分超时解
#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n, m;cin >> n >> m;vector<vector<double>> operation(n, vector<double>(2));double x, y;for(int i = 0; i < n; i++){cin >> operation[i][0] >> operation[i][1];}int i, j;for(int t = 0; t < m; t++){cin >> i >> j >> x >> y;double xx = x, yy = y;double angle = 0, k = 1;i--;for(;i < j; i++){if(operation[i][0] == 1){k *= operation[i][1];}else if(operation[i][0] == 2){angle += operation[i][1];}}if(k != 1){x *= k;y *= k;}if(angle != 0){xx = x * cos(angle) - y * sin(angle);yy = x * sin(angle) + y * cos(angle);cout << fixed << setprecision(3) << xx << " " << yy << endl;}else{cout << fixed << setprecision(3) << x << " " << y << endl;}}return 0;
}
100分解
#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n, m;cin >> n >> m;vector<double> A(n + 1, 1);//拉伸k倍vector<double> B(n + 1, 0);//旋转角度double x, y;for(int i = 1; i <= n; i++){int a; double b;cin >> a >> b;if(a == 1){A[i] = b*A[i - 1];B[i] = B[i - 1];}else{A[i] = A[i - 1];B[i] = b + B[i - 1];}}int i, j;for(int t = 0; t < m; t++){cin >> i >> j >> x >> y;double xx = x, yy = y;double k = A[j]/A[i - 1], angle = B[j] - B[i - 1];if(k != 1){x *= k;y *= k;}if(angle != 0){xx = x * cos(angle) - y * sin(angle);yy = x * sin(angle) + y * cos(angle);cout << fixed << setprecision(3) << xx << " " << yy << endl;}else{cout << fixed << setprecision(3) << x << " " << y << endl;}}return 0;
}
202309-3 梯度求解
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1e9 + 7;int main() {vector<string> vec;stack<map<ll, ll>> st;int n, m, k;cin >> n >> m;string str, s;vector<int> a(n + 1, 0);//变量的值getchar();getline(cin, str);std::stringstream ss(str);while(ss >> s){vec.push_back(s);}while(m--){cin >> k;str = "x" + to_string(k);//求导变量for(int i = 1; i <= n; i++)cin >> a[i];for(int i = 0; i < vec.size(); i++){s = vec[i];map<ll, ll> mp;if(s == str){ //是求导变量mp[1] = 1;st.push(mp);}else if(s[0] == 'x'){ //是其他变量int d = stoi(s.substr(1));mp[0] = a[d] % mod;st.push(mp);}else if(s == "+" || s == "-" || s == "*"){//是运算符map<ll,ll> mp2 = st.top();st.pop();map<ll,ll> mp1 = st.top();st.pop();if(s == "+"){mp = mp1;for(auto it : mp2){mp[it.first] = (mp[it.first] + it.second) % mod;}}else if(s == "-"){mp = mp1;for(auto it : mp2){mp[it.first] = (mp[it.first] - it.second) % mod;}}else{for(auto it1 : mp1){for(auto it2 : mp2){mp[it1.first + it2.first] += it1.second * it2.second;mp[it1.first + it2.first] %= mod;}}}mp1.clear();mp2.clear();st.push(mp);}else{ //是数字ll d = stoll(s);mp[0] = d % mod;st.push(mp);}}map<ll,ll> mp = st.top(); //获得结果的一元表达式st.pop();ll ans = 0;for(auto it : mp){ll e = it.first, c = it.second;if(e > 0){ans = ans + c * e * pow(a[k], e - 1);ans %= mod;}}cout << (ans + mod) % mod << endl;mp.clear();}return 0;
}
相关文章:
)
ccfcsp-202309(1、2、3)
202309-1 坐标变换(其一) #include <bits/stdc.h> using namespace std; int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n, m;cin >> n >> m;int x, y;int opx 0, opy 0;for(int i 0; i < n; i){cin &g…...

数据结构--数据结构概述
一、数据结构三要素 1. 数据的逻辑结构 数据的逻辑结构是指数据元素之间的关系和组织方式,通常分为线性结构和非线性结构。 线性结构:例如线性表,其中数据元素按照顺序排列,彼此之间存在一对一的关系。 非线性结构:…...

Spring中的BeanFactoryAware
BeanFactoryAware 是 Spring 框架中的一个接口,用于在 Spring 容器中获取 BeanFactory 实例。实现这个接口的类可以在其属性被设置后获取到 BeanFactory,从而可以访问 Spring 容器中的其他 bean。 BeanFactoryAware 接口概述 BeanFactoryAware 接口位于…...

Neo4j service is not installed
问题: Starting Neo4j. Neo4j service is not installed Unable to start. See user log for details. Run with --verbose for a more detailed error message.解决: neo4j windows-service install neo4j start ok了...
)
LeetCode 3132.找出与数组相加的整数 II:排序+3次尝试(nlog n)
【LetMeFly】3132.找出与数组相加的整数 II:排序3次尝试(nlog n) 力扣题目链接:https://leetcode.cn/problems/find-the-integer-added-to-array-ii/ 给你两个整数数组 nums1 和 nums2。 从 nums1 中移除两个元素,并且所有其他元素都与变量…...

微信小程序--26(全局配置-1)
一、全局配置文件 1.标志 app.json 2.配置项 pages 记录当前小程序所有页面的存放路径 window 全局配置小程序窗口配置 tabBar 设置小程序底部的tabBar效果 style 是否启用新版本的组将样式 3.window 导航栏区域 navigationBar …...

汽车4S店管理系统-计算机毕设Java|springboot实战项目
🍊作者:计算机毕设残哥 🍊简介:毕业后就一直专业从事计算机软件程序开发,至今也有8年工作经验。擅长Java、Python、微信小程序、安卓、大数据、PHP、.NET|C#、Golang等。 擅长:按照需求定制化开发项目、 源…...

bug的常见排查和分析思路以及相关的原因分类
作为开发人员,经常会收到来自用户和QA,领导反馈的各种问题。 为了快速问题,我们有时需要站在更高的角度,更全面的看待问题。才能更快锁定问题。 具体的bug还需要结合企业实际业务情况,相关的框架,依赖库&…...

Nature:7个提升科研产出的实用建议
我是娜姐 迪娜学姐 ,一个SCI医学期刊编辑,探索用AI工具提效论文写作和发表。 一个值得思考的问题是:层出不穷的效率工具到底是提升还是降低了科研产出? 大学教授萨拉 (Sara) 描述了她典型的工作日场景:"…...

react-native从入门到实战系列教程-页面之间的跳转
路由的跳转,是app开发中需要处理的问题,一个页面不可能装下那么多的内容。在react-native中,我们使用的路由组件跟reactjs中还是有区别的,这里贴出官网的文档:https://reactnavigation.org/docs/navigating 实现效果 安装 按照官网的指导安装即可。代码实现 app.jsx中改造…...

HarmonyOS应用开发者高级认证(一)
1、依次点击A、B、C、D四个按钮,其中不会触发UI刷新的是: 答案: Button("C").onClick(() > {this.nameList[0].name "Jim"})分析:直接更新非一级数据不会触发UI刷新 2、如果要实现Row组件内的子元素均匀…...

【网络】套接字(socket)编程——UDP版
1.socket 1.1.什么是socket Socket 的中文翻译过来就是“套接字”。 套接字是什么,我们先来看看它的英文含义:插座。 Socket 就像一个电话插座,负责连通两端的电话,进行点对点通信,让电话可以进行通信,端…...

一篇文章让你彻底掌握 Shell
大家好,这里是 Lucifer三思而后行,专注于提升数据库运维效率。 文章目录 一篇文章让你彻底掌握 Shell简介什么是 shell什么是 shell 脚本Shell 环境指定脚本解释器 模式交互模式非交互模式 基本语法解释器注释echoprintfprintf 的转义符 变量变量命名原则…...

Java中的Collection集合:深入理解与应用
在Java中,Collection接口是Java集合框架(Java Collections Framework)的基石之一,它定义了一系列操作对象集合的方法,如添加、删除、遍历等。Collection接口是List、Set和Queue等具体集合类型的父接口,为Ja…...
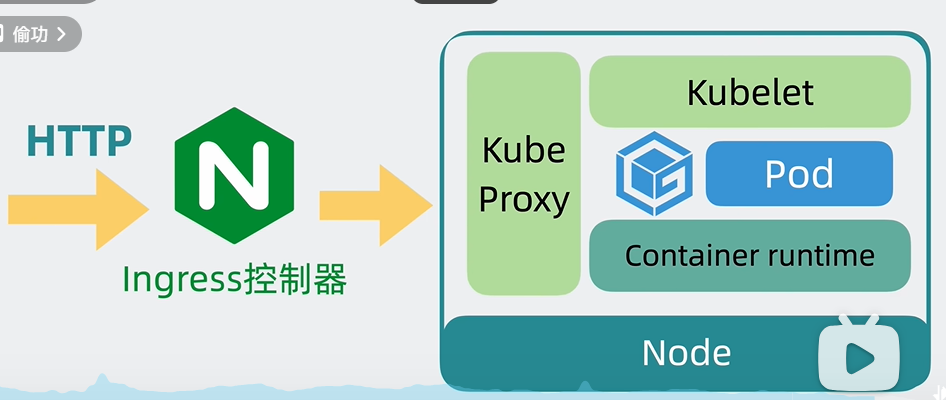
Kubernetes-K8S
Kubernetes由于单词太长,省略掉中间8个字母简称为K8S。它介于应用服务和服务器之间。能够通过策略协调和管理多个服务,只需要一个YAML文件配置。定义应用的部署顺序等信息,自动部署应用到各个服务器,还可以自动扩容缩容。 架构原理…...
简化文本处理流程,通用文字识别助力提升信息采集效率
随着信息技术的发展、移动设备使用的普及和全球化的商业需求,非结构化数据转换为结构化数据的需求日益增长,数字化成为信息存储和管理的主流趋势。在此背景下,OCR技术应运而生,该技术可以将图像中文本信息转化为计算机等设备可以使…...

【网络】TCP协议通信的重要策略——滑动窗口,快重传,流量控制,拥塞控制,延时应答
目录 MSS值 滑动窗口 滑动窗口与重发机制 快重传机制 滑动窗口与流量控制 滑动窗口与拥塞控制 延时应答 个人主页:东洛的克莱斯韦克-CSDN博客 相关文章 【网络】传输层TCP协议的报头和传输机制-CSDN博客 【网络】详解TCP协议通信时客户/服务端的状态-CSDN博…...

极狐GitLab CI/CD 如何构建镜像并推送到 azure 镜像仓库?
极狐GitLab 是 GitLab 在中国的发行版,专门面向中国程序员和企业提供企业级一体化 DevOps 平台,用来帮助用户实现需求管理、源代码托管、CI/CD、安全合规,而且所有的操作都是在一个平台上进行,省事省心省钱。可以一键安装极狐GitL…...

Leetcode—1143. 最长公共子序列【中等】
2024每日刷题(155) Leetcode—1143. 最长公共子序列 实现代码 class Solution { public:int longestCommonSubsequence(string text1, string text2) {int m text1.length();int n text2.length();vector<vector<int>> dp(m 1, vector&…...

ZBrush笔刷介绍
根据使用的方法和效果,ZBrush的笔刷可以分类如下: 基本功能笔刷 这些笔刷用于常规的雕刻、移动和平滑操作。 纹理应用笔刷 一般需要自己额外购买的是这三种笔刷 Alpha Brushes:使用灰度图(alpha)来定义笔刷形状和纹…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
