数据结构（11）——二叉搜索树

欢迎来到博主的专栏：数据结构
博主ID:代码小豪

---

二叉搜索树

二叉搜索树也称二叉排序树，是具备以下特征的二叉树
（1）每个节点最多拥有两个子节点
（2）对于每个节点，其左子树值均小于根节点，其右子树均大于根节点。

如图：

该二叉树为二叉搜索树，原因如下：
以节点8为根节点，其左子树均小于8，右子树均大于8.

以节点3为根节点，其左子树均小于3，其右子树均大于3.

以此类推。

该二叉树则不为二叉搜索树，因为以节点7为根节点，节点4小于7，却存在于根节点的右子树，因而不符合右子树均小于根节点这一特征。所以不构成搜索二叉树。

搜索二叉树有个重要的规则就是，在二叉树内不能存在两个相同值的节点，因为这会对二叉搜索树的删除结点造成影响。

二叉搜索树的声明与定义

二叉搜索树可以分为两部分，一部分是节点，另一部分则是树

对于节点，其需要记录一个值，以及分别指向左子节点与右子节点的两个指针。

再设计一个构造函数，通过传递key的值来生成该节点，并将左右指针置为空（方法不唯一，只是博主采用这种构造方式）

template<class k>
struct TreeNode
{TreeNode(const k& key):_key(key),_left(nullptr),_right(nullptr){}k _key;TreeNode* _left;TreeNode* _right;
};

接着是设计一个类来控制整个二叉搜索树，只需要定义一个指向二叉树的根节点的指针成员即可。此外，在设计一些搜索二叉树的成员函数，比如查找节点，排序节点，插入节点和删除结点。

template<class k>
class BSTree
{
public:typedef TreeNode<k> Node;//将节点类型重命名void find(const k& key);//查找void insert(const k& key);//插入节点void erase(const k& key);//删除结点void inorder();//中序遍历
private:Node* _root=nullptr;//根节点
};

二叉搜索树的查找

如何在二叉搜索树当中找到值为key的节点呢？当然，直接使用遍历的形式是可行的，但是利用二叉搜索树的特性可以更加高效。

用key值与根节点进行比较，会出现以下三种情况
（1）key比根节点大
（2）key比根节点小
（3）key等于根节点

如果是情况3，那就说明找到key值了，返回查找的结果

若是情况（1），根据二叉搜索树的特征，比根节点大的值都在右子树，因此进入右子树查找

若是情况（2），比根节点小的值都在左子树，因此进入左子树查找。

如果key来到了空节点处，就说明该二叉搜索树没有匹配的节点，因此查找的结果是无。

bool find(const k& key)//查找
{Node* cur = _root;while (cur != nullptr){if (key > cur->_key)//比key小，进入右树cur = cur->_right;if (key < cur->_key)//比key大，进入左树cur = cur->_left;else//与可以相等，返回结果return true;}return false;
}

动画演示1：假设key为7

演示动画2：假设key为9

其实二叉搜索树的查找方式和二分查找的原理非常类似，都是将查找数据的区间一步步缩短，最后确定元素。

二叉搜索树的插入

在二叉搜索树种插入新节点需要解决一个问题
（1）在插入新节点后，如何保持二叉搜索树的性质？

其实也就是搞清楚新节点插入的位置在哪，其实这个问题的解决思路可以参考前面查找节点的方法。

前面提到，通过缩短数据区间，可以在搜索二叉树中定位到元素的位置，我们可以假设待插入的节点已经存在于二叉树当中。通过查找该节点的方式，定位到元素的位置，然后将该节点插入到对应的位置即可。

思路如下：
（1）通过查找的方式缩短区间（即用key对比根节点）
（2）如果走到了空节点，就说明定位到了元素的位置，直接插入即可
（3）如果存在与插入节点相同值的节点，根据二叉搜索树不能存在两个相同节点的特性，停止不合法的插入操作

还存在一种特殊情况，即当二叉搜索树为空树时，此时无法通过查找的方式进行搜索（因为要让key和根节点的值进行比较，但是空树没有根节点），解决方法是直接生成根节点即可。

bool insert(const k& key)//插入节点
{if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (cur != nullptr){if (key > cur->_key)//比key小，进入右树{parent = cur;cur = cur->_right;}else if (key < cur->_key)//比key大，进入左树{parent = cur;cur = cur->_left;}else//与key相等，不合法的插入操作return false;}//来到空节点处，将新节点插入至该处cur = new Node(key);if (key > parent->_key)parent->_right = cur;elseparent->_left = cur;return true;
}

动画演示：

二叉搜索树的中序遍历

中序遍历二叉搜索树，会得到一个升序的结果，先来写出代码，再分析原理。

void inorder()//中序遍历
{_inorder(_root);
}
void _inorder(Node* root)
{if (root == nullptr)return;_inorder(root->_left);cout << root->_key<<' ';_inorder(root->_right);
}

执行如下操作：

int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
BSTree<int> b;
for (auto e : arr)
{b.insert(e);
}

上述代码的作用是构造出下图的二叉搜索树

再中序遍历该二叉搜索树

b.inorder();

运行结果为：

那么为什么中序遍历会呈现出升序的特征呢？

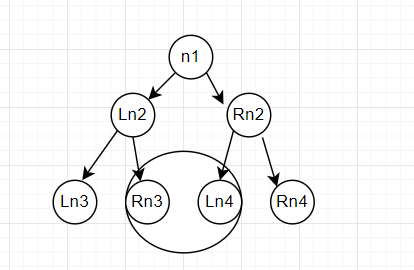
根据二叉搜索树的定义，对于每个根节点来说，其左子树小于根节点，其右子树大于根节点。那么下面这个二叉树的排序为

Ln2<n1<Rn2

Ln3<Ln2<Rn3<n1<Ln4<Rn2<Rn4.

把小于号去掉，即为
Ln3 Ln2 Rn3 n1 Ln4 Rn2 Rn4.
这个顺序既符合中序遍历的顺序，也符合升序的顺序。我们也可以由此得出一个结论

离根节点越左的节点，越小，离根节点越右的节点，越大，越靠近根节点的节点，越接近根节点。比如上图中的Ln4和Rn3.

这个结论将会在二叉搜索树的删除中起到非常大的左右。

二叉搜索树的删除

首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情况：

a. 要删除的结点无子结点

解决方法：直接删除即可。

b. 要删除的结点只有左子结点

删除该结点且使被删除节点的父结点指向被删除节点的左子结点

c. 要删除的结点只有右子结点

删除该结点且使被删除节点的父结点指向被删除结点的右子结点

看起来有待删除节点有4中情况，实际情况a可以与情况b或者c合并起来。

d. 要删除的结点有左、右孩子结点

这种情况下是最麻烦的，因为我们不能贸然的将节点3删除，这会断开二叉搜索树与节点3的左右子树的链接，破坏结构。

换句话说，要删除节点3，就要找到一个节点来替换节点3，这样才能保持住二叉搜索树的特性。那么什么节点可以胜任呢？

为了维持二叉搜索树的特性，因此替换节点的节点应该有以下特征：（1）比左子节点大（2）比右子节点小。因此选取来替换的节点应该越接近待删除的节点越好。

在上一节中提到，越接近根节点的节点，其值也越接近根节点。对于待删除的节点来说，最接近它的值无非两个
（1）其左子树最右边的节点
（2）其右子树最左边的节点
这两个节点都是离待删除节点最近的节点。也是值最接近的节点。因此，选取这两个节点来替换待删除的节点再合适不过了。

删除操作的实现如下：

bool erase(const k& key)//删除结点{Node* cur = _root;Node* parent = cur;while (cur != nullptr){if (key > cur->_key)//比key小，进入右树{parent = cur;cur = cur->_right;}if (key < cur->_key)//比key大，进入左树{parent = cur;cur = cur->_left;}else//与key相等，删除该节点{if (cur->_left == nullptr)//情况a、bif (parent->_left = cur)parent->_left = cur->_right;elseparent->_right = cur->_right;else if(cur->_right==nullptr)//情况cif (parent->_left = cur)parent->_left = cur->_left;elseparent->_right = cur->_left;else//情况d{Node* RightMinp = cur;//右子树的最左节点的父节点Node* RightMin = cur->_right;//右子树的最左节点while (RightMin->_left != nullptr){RightMinp = RightMin;RightMin = RightMin->_left;}cur->_key = RightMin->_key;//交换节点if (RightMinp->_right == RightMin)RightMinp->_right = RightMin->_right;elseRightMinp->_left = RightMin->_right;delete RightMin;}return true;}}return false;}