数据结构初阶——算法复杂度超详解
文章目录
- 1. 数据结构前言
- 1. 1 数据结构
- 1. 2 算法
- 2. 算法效率
- 2. 1 复杂度的概念
- 3. 时间复杂度
- 3. 1 大O的渐进表示法
- 3. 2 时间复杂度计算示例
- 3. 2. 1 示例1
- 3. 2. 2 示例2
- 3. 2. 3 示例3
- 3. 2. 4 示例4
- 3. 2. 5 示例5
- 3. 2. 6 示例6
- 3. 2. 7 示例7
- 4. 空间复杂度
- 4. 1 空间复杂度计算示例
- 4. 1. 1 示例1
- 4. 1. 2 示例2
- 5. 常见复杂度对比
- 6.复杂度算法题——[旋转数组](https://leetcode.cn/problems/rotate-array/description/)
- 思路1
- 思路2
- 思路3
1. 数据结构前言
1. 1 数据结构
数据结构是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。没有一种单一的数据结构对所有用途都有用,所以我们要学各式各样的数据结构,
如:线性表、树、图、哈希等
1. 2 算法
算法就是定义良好的计算过程,它取一个或一组的值为输入,并产生出一个或一组值作为输出。
简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
2. 算法效率
如何衡量一个算法的好坏呢?
案例:旋转数组
思路:循环K次将数组所有元素向后移动一位
如果你使用用这个代码:
void rotate(int* nums, int numsSize, int k) {while (k--){//循环内部将所有元素向后移动一位int end = nums[numsSize - 1];for (int i = numsSize - 1; i > 0; i--){nums[i] = nums[i - 1];}nums[0] = end;}
}
代码点击执行可以通过,然而点击提交却无法通过(超时),那该如何衡量其好与坏呢?

2. 1 复杂度的概念
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源。因此衡量一个算法的好
坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。
在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度(虽然话是这么说,但实际上在OJ题和面试中有很多题目都会要求空间复杂度以强迫优化算法,校验程序员的能力)。
3. 时间复杂度
定义:在计算机科学中,算法的时间复杂度是一个函数式T(N),它定量描述了该算法的运行时间。时间复杂度是衡量程序的时间效率,那么为什么不去计算程序的运行时间呢?
- 因为程序运行时间和编译环境和运行机器的配置都有关系,比如同一个算法程序,用一个老编译器进行编译和新编译器编译,在同样机器下运行时间不同。
- 同一个算法程序,用一个老低配置机器和新高配置机器,运行时间也不同。
- 并且时间只能程序写好后测试,不能写程序前通过理论思想计算评估。
那么算法的时间复杂度是一个函数式T(N)到底是什么呢?
这个T(N)函数式计算了程序的执行次数。在C语言编译链接中,我们知道算法程序被编译后生成二进制指令,程序运行,就是cpu执行这些编译好的指令。那么我们通过程序代码或者理论思想计算出程序的执行次数的函数式T(N),假设每句指令执行时间基本一样(实际中有差别,但是微乎其微),那么执行次数和运行时间就是等比正相关。
这样也脱离了具体的编译运行环境,执行次数就可以代表程序时间效率的优劣。
比如解决一个问题的算法a程序T(N)=N,算法b程序T(N)=N^2,那么算法a的效率一定优于算法b。
举例:
//计算一下 Func1 中 ++count 语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}
}
Func1 执行的基本操作次数:
T(N) = N ^ 2 + 2 * N + 10
N = 10,T(N) = 130
N = 100,T(N) = 10210
N = 1000 ,T(N) = 1002010
通过对N取值分析,对结果影响最大的一项是 N2 这一项。
实际中我们计算时间复杂度时,计算的也不是程序的精确的执行次数,精确执行次数计算起来还是很麻烦的(不同的一句程序代码,编译出的指令条数都是不一样的),计算出精确的执行次数意义也不大,因为我们计算时间复杂度只是想比较算法程序的增长量级,也就是当N不断变大时T(N)的差别,上面我们已经看到了当N不断变大时常数和低阶项对结果的影响很小,所以我们只需要计算程序能代表增长量级的大概执行次数,复杂度的表示通常使用大O的渐进表示法。
3. 1 大O的渐进表示法
大O符号(Big O notation)是用于描述函数渐进行为的数学符号。
推导大O阶规则:
- 时间复杂度函数式T(N)中,只保留最高阶项,去掉那些低阶项,因为当N不断变大时,低阶项对结果影响越来越小,当N无穷大时,就可以忽略不计了。
- 如果最高阶项存在且不是1,则去除这个项目的常数系数,因为当N不断变大,这个系数对结果影响越来越小,当N无穷大时,就可以忽略不计了。
- T(N)中如果没有N相关的项目,只有常数项,用常数1取代所有加法常数。
通过以上方法,可以得到 Func1 的时间复杂度为:O(n2)。
3. 2 时间复杂度计算示例
3. 2. 1 示例1
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k)++count;int M = 10;while (M--)++count;printf("%d\n", count);
}
很容易知道,F(N) = 2 * N + 10 。
根据推导规则第3条得出Func2的时间复杂度为:O(N)。
3. 2. 2 示例2
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k)++count;for (int k = 0; k < N; ++k)++count;printf("%d\n", count);
}
Func3执行的基本操作次数:F(N) = M + N
因此,Func3的时间复杂度为:O(N)。
3. 2. 3 示例3
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k)++count;printf("%d\n", count);
}
Func4执行的基本操作次数:F(N) = 100。
根据推导规则第1条得出Func2的时间复杂度为:O(1)。
3. 2. 4 示例4
const char* strchr(const char* str, int character)
{const char* p_begin = str;while (*p_begin != character){if (*p_begin == '\0')return NULL;p_begin++;}return p_begin;
}
这个代码我们来细致地分析一下:
这是一个在字符串中寻找特定字符的函数,如果找到了,就返回这个字符在字符串中首次出现的地址,否则返回 NULL,因此它的运行次数更加复杂,需要分类讨论:
strchr执行的基本操作次数:
- 若要查找的字符在字符串第一个位置,则:
F(N) = 1 - 若要查找的字符在字符串最后的一个位置,则:
F(N) = N - 若要查找的字符在字符串中间位置,则:
F(N) = N / 2
这也就意味着,我们不能用一个关系式表达出 strchr 这个函数的时间复杂度:
最好情况:O(1)
最坏情况:O(N)
平均情况:O(N)
通过上面这个函数我们会发现,有些算法的时间复杂度存在最好、平均和最坏情况。
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
大O的渐进表示法在实际中一般情况关注的是算法的上界,也就是最坏运行情况。
3. 2. 5 示例5
//冒泡排序
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);//Swap 函数的定义就省略了,想必各位都知道exchange = 1;}}if (exchange == 0)break;}
}
BubbleSort执行的基本操作次数:
- 若数组有序,则:
F(N) = N - 若数组有序且为降序,则:
F(N) = N * (N + 1) / 2 - 若要查找的字符在字符串中间位置,则介于其他两种情况之间
因此,BubbleSort的时间复杂度取最差情况为:O(N2)
3. 2. 6 示例6
void func5(int n)
{int cnt = 1;while (cnt < n)cnt *= 2;
}
- 当
n=2时,执行次数为 1 - 当
n=4时,执行次数为 2 - 当
n=16时,执行次数为4 - 假设执行次数为
x,则 2x = n
因此执行次数:x=logn
因此:func5的时间复杂度取最差情况为O(logn)
注意博客中和书籍中
l o g 2 n , l o g n , l g n log_2{n},log{n},lg{n} log2n,logn,lgn
的表示
当n接近无穷大时,底数的大小对结果影响不大。因此,一般情况下不管底数是多少都可以省略不写,即可以表示为 logn
不同书籍的表示方式不同,以上写法差别不大,我建议使用logn
3. 2. 7 示例7
//阶乘
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
调用一次Fac函数的时间复杂度为 O(1)
而在Fac函数中,存在n次递归调用Fac函数
因此:阶乘递归的时间复杂度为:O(n)
4. 空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中因为算法的需要额外临时开辟的空间的估算。
空间复杂度不是程序占用了多少bytes的空间,因为常规情况每个对象大小差异不会很大,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
4. 1 空间复杂度计算示例
4. 1. 1 示例1
//计算BubbleSort的时间复杂度
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
函数栈帧在编译期间已经确定好了,只需要关注函数在运行时额外申请的空间。
BubbleSort额外申请的空间有exchange等有限个局部变量,使用了常数个额外空间。
因此空间复杂度为 O(1)。
4. 1. 2 示例2
// 计算阶乘递归Fac的空间复杂度
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
Fac递归调用了N次,额外开辟了N个函数栈帧,每个栈帧使用了常数个空间。
因此空间复杂度为:O(N)
这里你可能会有疑惑:为什么在冒泡排序中函数栈帧就忽略,而在递归中就要计算?
因为一个函数栈帧的空间复杂度是一个常数,在冒泡排序中只创建了一次函数栈帧,所以函数栈帧总的使用的空间为常数,忽略不计。
但在递归中,函数栈帧创建了N次,就不是常数了,所以要计算。
5. 常见复杂度对比


图源网络,通过这两张图可以很清晰地看出不同复杂度的算法的快慢,大概了解一下就好,在后续使用中会自然地加强记忆。
6.复杂度算法题——旋转数组
思路1
时间复杂度 O(n2)
循环K次将数组所有元素向后移动一位(代码不通过)
void rotate(int* nums, int numsSize, int k) {while (k--){//循环内部将所有元素向后移动一位int end = nums[numsSize - 1];for (int i = numsSize - 1; i > 0; i--){nums[i] = nums[i - 1];}nums[0] = end;}
}
思路2
空间复杂度 O(n)
申请新数组空间,先将后k个数据放到新数组中,再将剩下的数据挪到新数组中
void rotate(int* nums, int numsSize, int k)
{//这个写法在LeetCode上可以运行,但在VS上无法运行,因为这是C99引入的变长数组,VS没有相关实现//int newArr[numsSize];//在VS上可以使用动态内存管理来模拟实现变长数组int* newArr = (int*)malloc(sizeof(int) * numsSize);for (int i = 0; i < numsSize; ++i)newArr[(i + k) % numsSize] = nums[i];for (int i = 0; i < numsSize; ++i)nums[i] = newArr[i];//最后不要忘记释放空间free(newArr);newArr = NULL;
}
思路3
空间复杂度 O(1)
前n-k个逆置:4321 567
后k个逆置:4321 765
整体逆置:5671234
这样也可以实现题目要求。
void reverse(int* nums, int begin, int end)
{//reverse函数用来颠倒一个范围内的数组顺序while (begin < end) {//下面3行是交换int tmp = nums[begin];nums[begin] = nums[end];nums[end] = tmp;begin++;end--;}
}
void rotate(int* nums, int numsSize, int k)
{k = k % numsSize; //防止 k > numsSize 导致程序错误,k % numsSize 就是实际要转动的次数reverse(nums, 0, numsSize - k - 1);reverse(nums, numsSize - k, numsSize - 1);reverse(nums, 0, numsSize - 1);
}
谢谢你的阅读,喜欢的话来个点赞收藏评论关注吧!
我会持续更新更多优质文章
相关文章:

数据结构初阶——算法复杂度超详解
文章目录 1. 数据结构前言1. 1 数据结构1. 2 算法 2. 算法效率2. 1 复杂度的概念 3. 时间复杂度3. 1 大O的渐进表示法3. 2 时间复杂度计算示例3. 2. 1 示例13. 2. 2 示例23. 2. 3 示例33. 2. 4 示例43. 2. 5 示例53. 2. 6 示例63. 2. 7 示例7 4. 空间复杂度4. 1 空间复杂度计算…...
布局 4 预定义的形状和箭头)
ArcGIS Pro SDK (十二)布局 4 预定义的形状和箭头
ArcGIS Pro SDK (十二)布局 4 预定义的形状和箭头 文章目录 ArcGIS Pro SDK (十二)布局 4 预定义的形状和箭头1 创建预定义的形状图形元素2 创建预定义的形状图形元素3 创建预定义的形状图形元素4 创建线箭头元素环境:Visual Studio 2022 + .NET6 + ArcGIS Pro SDK 3.0 1 …...

在 Ubuntu 14.04 服务器上安装 ISPConfig3 的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 虽然命令行是一个强大的工具,可以让您在许多情况下快速轻松地工作,但在某些情况下,可视化界面…...

ELK学习笔记
ElasticStack分布式日志系统概述 Elasticsearch: 一个分布式搜索引擎,能够快速存储、搜索和分析大量数据。核心概念包括索引(Index)、文档(Document)和分片(Shard)。使用 RESTful API 进行数据操…...
Python+Selenium+Pytest+POM自动化测试框架封装详解
1、测试框架简介 1)测试框架的优点 代码复用率高,如果不使用框架的话,代码会显得很冗余。可以组装日志、报告、邮件等一些高级功能。提高元素等数据的可维护性,元素发生变化时,只需要更新一下配置文件。使用更灵活的…...

Hidden Marlov Model(HMM)
一、Model 1、将声学特征设为X,经过语音识别得到的tokens设为Y,目标是找到通过X得到Y的最大概率,可以通过概率公式改变为 分为两个概率 2、将tokens序列Y转化为states序列S,声学特征分得更细 3、从states到声学特征的过程 二、HM…...

mamba的安装及下载速度慢问题解决
同事反馈mamba的安装时网络慢 mamba是conda的加速工具,相比于conda 对包和环境的管理,mamba可以实现并行运算。相比于 conda,mamba 是用C重写了 conda 的部分功能,运行效率显著提高,可以进行并行的下载,使…...
【Linux入门】Linux环境搭建
目录 前言 一、发行版本 二、搭建Linux环境 1.Linux环境搭建方式 2.虚拟机安装Ubuntu 22.02.4 1)安装VMWare 2)下载镜像源 3)添加虚拟机 4)换源 5)安装VM Tools 6)添加快照 总结 前言 Linux是一款自由和开放…...

CPU缓存一致性机制详解
CPU缓存一致性机制详解 在多核处理器中,缓存一致性是保证系统正常运行的重要环节。本文详细介绍了缓存一致性协议、写入策略、总线嗅探、目录协议等相关概念,并通过示例代码解释了这些机制是如何在实际应用中工作的。通过学习本文,读者可以深…...

Android 12系统源码_屏幕设备(一)DisplayManagerService的启动
前言 DisplayManagerService是Android Framework中管理显示屏幕相关的模块,各种Display的连接、配置等,都是通过DMS和来管理控制。 在DMS模块中,对显示屏幕的描述分为物理显示屏(physical display)和逻辑显示屏(logical display),…...

《AI视频类工具之十——D-ID》
一.简介 官网:D-ID | The #1 Choice for AI Generated Video Creation Platform D-ID是一个人工智能生成的视频创建平台,可以轻松快速地从文本输入中创建高质量、高性价比和引人入胜的视频,背后的Al技术是由Stable Difusion和GPT.3提供支持,可以在没有任何技术知识的情况…...
【网络】局域网LAN、广域网WAN、TCP/IP协议、封装和分用
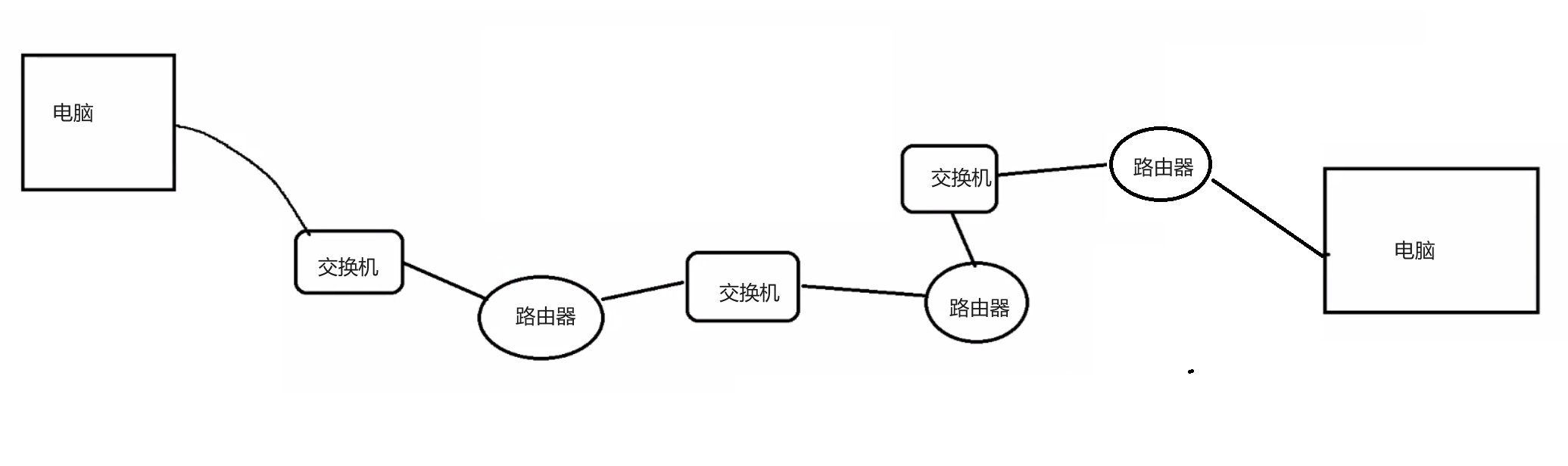
文章目录 局域网 LAN广域网 WAN网络中的重要概念IP 地址端口号 认识协议协议分层是什么OSI 七层网络模型TCP/IP 五层网络模型(或四层)物理层传输层网络层数据链表层应用层网络设备所在分层 封装和分用[站在发送方视角](封装)[站在…...

我司搜索中台的三次演变
本人从入职就开始负责我司的搜索中台了,总共是经历了三个大版本的迭代。 分别是: 基于阿里云智能开放搜索OpenSearch实现的第一代自研,开源canal(数据同步) 底层阿里云elasticsearch 对索引封装 实现的第二代自研&a…...

html+css+js网页设计 电商模版4个页面
htmlcssjs网页设计 电商模版4个页面 带js 网页作品代码简单,可使用任意HTML编辑软件(如:Dreamweaver、HBuilder、Vscode 、Sublime 、Webstorm、Text 、Notepad 等任意html编辑软件进行运行及修改编辑等操作)。 获取源码 1&…...

区块链技术在Facebook中的潜力:未来趋势与挑战
数据安全的新高度 区块链技术以其去中心化和不可篡改的特性,正在成为提升数据安全和隐私保护的重要工具。Facebook作为全球最大的社交媒体平台之一,正积极探索如何将区块链技术应用于其平台,以增强用户数据的安全性和隐私保护。Facebook在应…...

dockerfile自定义镜像
目录 概念 基于dockerfile创建 dockerfile的命令 构建容器 FROM ENTRYPOINT和CMD RUN COPY和ADD 工作目录和环境变量以及容器卷(挂载卷) EXPOSE 实战 概念 dockerfile就是自定义镜像,通过dockerfile创建的都是镜像,而…...

【工作状态】如何保持专注?
好的睡眠计划主题化 1、保持足够的睡眠,才能头脑清晰和有精力,工作不是纯拼体力,要用脑力的。 2、脑力主要工作放在午餐前,在脑力充足的时候使用脑力,下午五点后可以安排脑力活动较低的工作,比如听课读书。…...

欧科云链研究院对话:风浪越大鱼越贵—链上数据洞悉加密市场规律
作者 Hedy 出品 OKG Research “我们从来就不是理性人。但可以用最简单的工具——链上数据做‘最猛’的分析。” 在经历了超级宏观周之后,金融市场产生了巨大的震荡,加密市场的表现也越来越受到宏观经济因素的影响。欧科云链研究院OKG Research 集结多…...

SQLite库笔记:日期和时间函数
1. 函数概述 SQLite支持7个日期和时间函数,如下: 1 date(time-value, modifier, modifier, ...) 返回YYYY-MM-DD格式的日期 2 time(time-value, modifier, modifier, ...) 返回HH:MM:SS格式的时间 3 datetime(time-value, modifier, modifier, ...…...

Linux开发板运行报错/system/bin/sh: can‘t create /dev/leds: Permission denied
Linux开发板运行报错/system/bin/sh: cant create /dev/leds: Permission denied 1.问题解决 1.问题解决 /system/bin/sh: can’t create /dev/leds: Permission denied 在linux开发板下运行驱动报错没有权限,需要运行 su,同时也会停止打印 在运行: ch…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
