24/8/15算法笔记 dp策略迭代 价值迭代
-
策略迭代:
- 策略迭代从某个策略开始,计算该策略下的状态价值函数。
- 它交替进行两个步骤:策略评估(Policy Evaluation)和策略改进(Policy Improvement)。
- 在策略评估阶段,计算给定策略下每个状态的期望回报。
- 在策略改进阶段,尝试找到一个更好的策略,该策略对于每个状态选择最优动作。
- 这个过程一直进行,直到策略收敛,即不再有改进的空间。
-
价值迭代:
- 价值迭代直接迭代状态价值函数,而不是策略。
- 它从任意状态价值函数开始,然后迭代更新每个状态的价值,直到收敛。
- 在每次迭代中,对所有状态使用贝尔曼最优性方程(Bellman Optimality Equation)来更新其价值。
- 价值迭代通常比策略迭代更快收敛到最优价值函数。
-
收敛性:
- 策略迭代保证在有限次迭代后收敛到最优策略和最优价值函数。
- 价值迭代也保证收敛,但收敛速度可能因问题而异。
-
计算复杂度:
- 策略迭代可能需要多次策略评估,每次评估都涉及对所有状态的操作,因此在某些情况下可能比较慢。
- 价值迭代每次迭代只更新一次所有状态的价值,但可能需要更多次迭代才能收敛。
-
适用性:
- 策略迭代在策略空间较大或状态转移概率较复杂时可能更有效。
- 价值迭代适用于状态空间较大且容易计算贝尔曼最优性方程的情况。
-
实现方式:
- 策略迭代通常使用循环,外部循环负责策略评估,内部循环负责策略改进。
- 价值迭代使用单一循环,每次迭代更新所有状态的价值。
策略迭代:
#获取一个格子的状态
def get_state(row,col):if row !=3:return'ground'if row ==3 and col ==0:return 'ground'if row==3 and col==11:return 'terminal'return 'trap'
get_state(0,0)地图上有平地,陷阱,终点
#在一个格子里做动作
def move(row,col,action):#如果当前已经在陷阱或者终点,则不能执行任何动作,反馈都是0if get_state(row,col)in['trap','terminal']:return row,col,0#向上if action==0:row-=1#向下if action ==1:row+=1#向左if action==2:col-=1#向右if action==3:col+=1#不允许走到地图外面去row = max(0,row)row = min(3,row)col =max(0,col)col =min(11,col)#是陷阱的话,奖励是-100,否则都是-1#这样强迫了机器尽快结束游戏,因为每走一步都要扣一分#结束最好是以走到终点的形式,避免被扣100分reward = -1if get_state(row,col)=='trap':reward -=100return row,col,reward
import numpy as np#初始化每个格子的价值
values = np.zeros([4,12])#初始化每个格子下采用动作的概率
pi = np.ones([4,12,4])*0.25values,pi[0]
#Q函数,求state,action的分数
#计算在一个状态下执行动作的分数
def get_qsa(row,col,action):#当前状态下执行动作,得到下一个状态和rewardnext_row,next_col,reward = move(row,col,action)#计算下一个状态分数,取values当中记录的分数即可,0.9是折扣因子value = values[next_row,next_col]*0.9#如果下个状态是终点或者陷阱,则下一个状态分数为0if get_state(next_row,next_col)in ['trap','terminal']:value = 0#动作的分数本身就是reward,加上下一个状态的分数return value + reward
get_qsa(0,0,0)-1.0
#策略评估
def get_values():#初始化一个新的values,重新评估所有格子的分数new_values = np.zeros([4,12])#遍历所有格子for row in range(4):for col in range(12):#计算当前格子4个动作分别的分数action_value = np.zeros(4)#遍历所有动作for action in range(4):action_value[action] = get_qsa(row,col,action)#每个动作的分数和它的概率相乘action_value *=pi[row,col]#最后这个格子的分数,等于该格子下所有动作的分数求和new_values[row,col] = action_value.sum()return new_values
get_values()
#策略提升函数
def get_pi():#重新初始化每个格子下采用动作的概率,重新评估new_pi = np.zeros([4,12,4])#遍历所有格子for row in range(4):for col in range(12):#计算当前格子4个动作分别的分数action_value = np.zeros(4)#遍历所有动作for action in range(4):action_value[action] = get_qsa(row,col,action)#计算当前状态下,达到最大分数的动作有几个count = (action_value == action_value.max()).sum()#让这些动作均分概率for action in range(4):if action_value[action]==action_value.max():new_pi[row,col,action] = 1/countelse:new_pi[row,col,action]=0return new_pi
get_pi()
#循环迭代策略评估和策略提升,寻找最优解
for _ in range(10):for _ in range(100):values = get_values()pi = get_pi()
values,pi
#打印游戏,方便测试
def show(row,col,action):graph=['','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','2','2','2','2','2', '2','2','2','2','2','1']action = {0:'上',1:'下',2:'左',3:'右'}[action]graph[row*12+col] = actiongraph=' '.join(graph)for i in range(0,4*12,12):print(graph[i:i+12])show(1,1,0)#测试函数
from IPython import display
import timedef test():#起点在0,0row = 0col = 0#最多玩N步for _ in range(200):#选择一个动作action = np.random.choice(np.arange(4),size = 1,p=pi[row,col])[0]#打印这个动作display.clear_output(wait = True)time.sleep(1)show(row,col,action)#执行动作row,col,reward = move(row,col,action)#获取当前状态,如果状态是终点或者掉到陷阱则终止if get_state(row,col) in ['trap','terminal']:break
test()价值迭代算法:
def get_values():#初始化一个新的values,重新评估所有格子的分数new_values = np.zeros([4,12])#遍历所有格子for row in range(4):for col in range(12):#计算当前格子4个动作分别的分数action_value = np.zeros(4)#遍历所有动作for action in range(4):action_value[action] = get_qsa(row,col,action)"""和策略迭代算法唯一的不同点"""#求每一个格子的分数,等于该格子下所有动作的最大分数new_values[row,col] = action_value.max()return new_values
get_values()
相关文章:

24/8/15算法笔记 dp策略迭代 价值迭代
策略迭代: 策略迭代从某个策略开始,计算该策略下的状态价值函数。它交替进行两个步骤:策略评估(Policy Evaluation)和策略改进(Policy Improvement)。在策略评估阶段,计算给定策略下…...

【MMdetection改进】换遍MMDET主干网络之SwinTransformer-Tiny(基于MMdetection)
OpenMMLab 2.0 体系中 MMYOLO、MMDetection、MMClassification、MMSelfsup 中的模型注册表都继承自 MMEngine 中的根注册表,允许这些 OpenMMLab 开源库直接使用彼此已经实现的模块。 因此用户可以在MMYOLO 中使用来自 MMDetection、MMClassification、MMSelfsup 的主…...

FL Studio21.2.4最新中文版免费下载汉化包破解补丁
🎉 FL Studio 21中文版新功能全解析!让你的音乐制作更加高效! 嘿,各位音乐制作的小伙伴儿们,今天我要安利一款你们绝对会爱上的神器——FL Studio 21中文版!这款软件不仅功能强大,而且操作简便…...

私域场景中的数字化营销秘诀
在当今的商业世界,私域场景的营销变得愈发重要。今天咱们就来深入探讨一下私域场景中的几个关键营销手段。 一、会员管理与营销 企业一旦拥有完善的会员体系,数字化手段就能大放异彩。它可以助力企业对会员进行精细划分,深度了解会员的消费…...

一键换肤(Echarts 自定义主题)
一键换肤(Echarts 自定义主题) 一、使用官方主题配置工具 官方主题配置工具:https://echarts.apache.org/zh/theme-builder.html 如果以上主题不满足使用,可以自己自定义主题 例如:修改背景、标题等,可…...
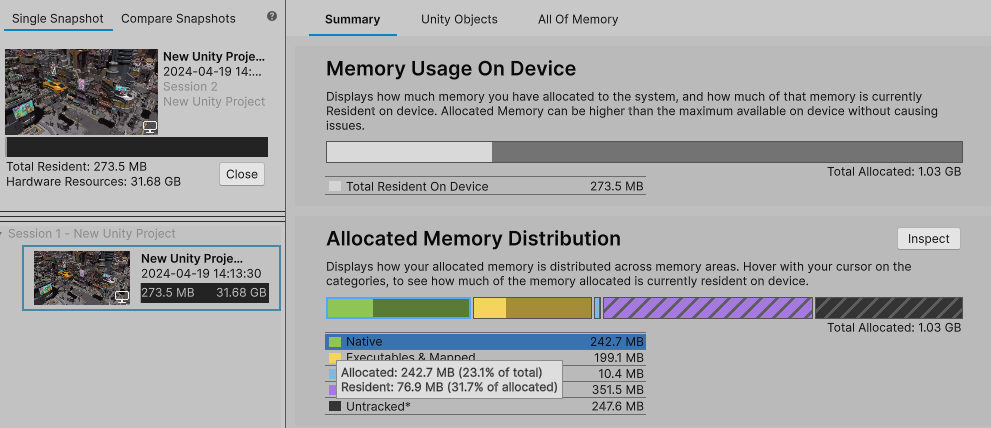
Unity 6 预览版正式发布
Unity 6 预览版发布啦,正式版本将于今年晚些时候正式发布! 下载链接: https://unity.com/releases/editor/whats-new/6000.0.0 Unity 6 预览版是 Unity 6 开发周期的最后一个版本,在去年 11 月 Unite 大会上,我们宣…...

如何跳过极狐GitLab 密钥推送保护功能?
极狐GitLab 是 GitLab 在中国的发行版,专门面向中国程序员和企业提供企业级一体化 DevOps 平台,用来帮助用户实现需求管理、源代码托管、CI/CD、安全合规,而且所有的操作都是在一个平台上进行,省事省心省钱。可以一键安装极狐GitL…...
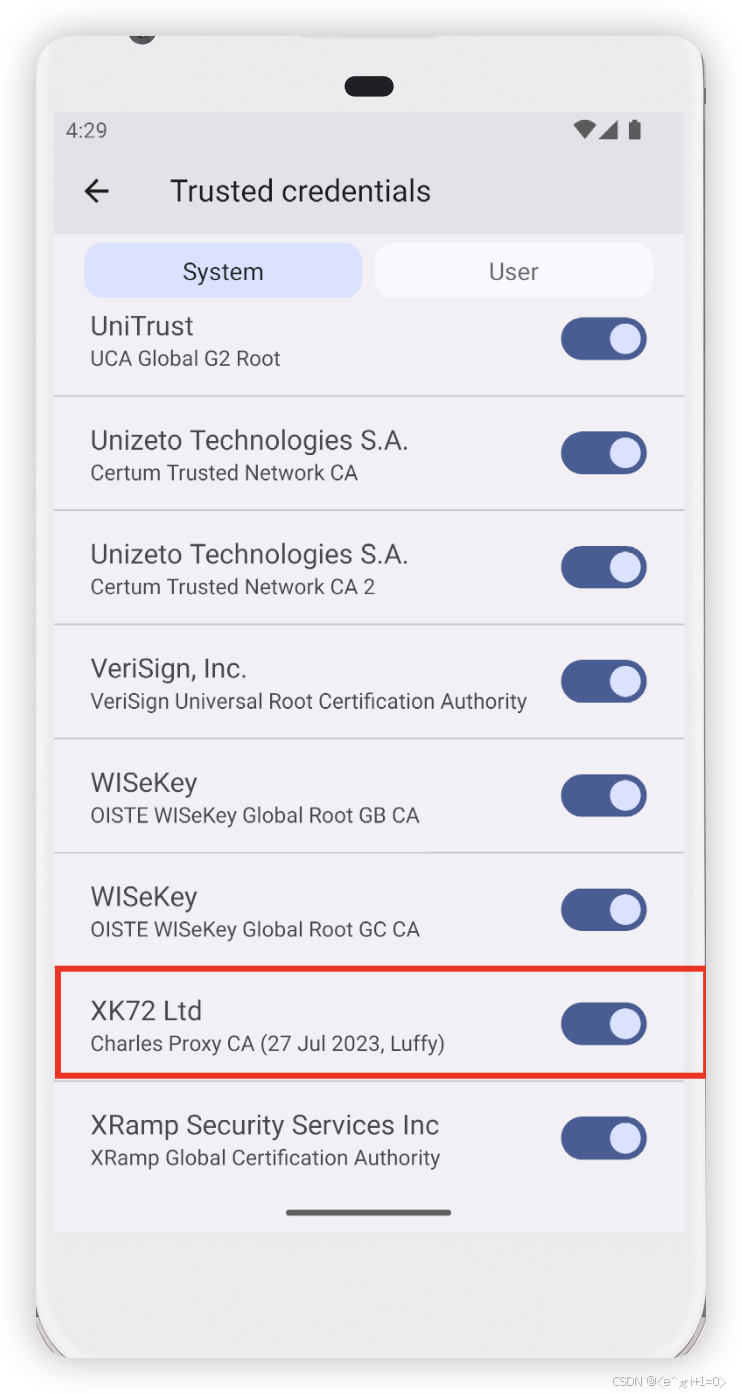
Android高版本抓包总结
方案1 CharlesVirtualXposedJustTrustMe 推荐使用三星手机此方案 VirtualXposed下载链接:https://github.com/android-hacker/VirtualXposed/releases JustTrustMe下载链接:https://github.com/Fuzion24/JustTrustMe/releases/ 下载完成后使用adb命令…...
《AI视频类工具之五—— 开拍》
一.简介 官网:开拍 - 用AI制作口播视频用AI制作口播视频https://www.kaipai.com/home?ref=ai-bot.cn 开拍是一款由美图公司在2023年推出,利用AI技术制作的短视频分享应用。这款工具通过AI赋能,为用户提供了从文案创作、视频拍摄到视频剪辑、包装的一站式解决方案,极大地…...

面试经典算法150题系列-最后一个单词的长度
最后一个单词的长度 给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。 示例 1: 输入:s "Hello World&qu…...

RTT学习
电源管理组件 嵌入式系统低功耗管理的目的在于满足用户对性能需求的前提下,尽可能降低系统功耗以延长设备待机时间。 高性能与有限的电池能量在嵌入式系统中矛盾最为突出,硬件低功耗设计与软件低功耗管理的联合应用成为了解决矛盾的有效手段。 现在的各…...
|附赠完整面试流程)
前端面试题(二十五)|附赠完整面试流程
📝📝今日分享:前端面试题系列继续更新啦! 🤔🤔面试题是什么呢?这份前端面试题主要是上海某银行的中级前端面试题,面试时长属实没想到,挺短的!但从整个面试流程…...

【分布式系统】关于主流的几款分布式链路追踪工具
Jaeger 标准化与兼容性: Jaeger 支持 OpenTracing 和 OpenTelemetry 标准,这意味着它可以与各种微服务架构和应用框架无缝集成,提供了广泛的兼容性和灵活性。 数据存储选项: Jaeger 支持多种数据存储后端,如 Cassandra…...

【吸引力法则】探究人生欲:追求深度体验与宇宙链接
文章目录 什么是人生欲?唤醒人生欲:克服配得感的三大障碍1 第一大障碍:法执的压制2 第二大障碍:家庭的继承2.1 家庭创伤的代际传递2.2 家庭文化基因的传递2.2.1 “成年人最大的美德是让自己的生活过得更加精彩。”2.2.2 荷欧波诺波…...

REST framework-通用视图[Generic views]
Django’s generic views… were developed as a shortcut for common usage patterns… They take certain common idioms and patterns found in view development and abstract them so that you can quickly write common views of data without having to repeat yourself…...

行驶证OCR识别接口如何用Java调用
一、什么是行驶证OCR识别接口? 传入行驶证照片,行驶证图片上的文字信息,返回包括所有人、品牌型号、住址、车牌号、发动机号码、车辆识别代号、注册日期、发证日期等信息。 行驶证 OCR 接口的主要作用是代替手动输入,提高信息录…...
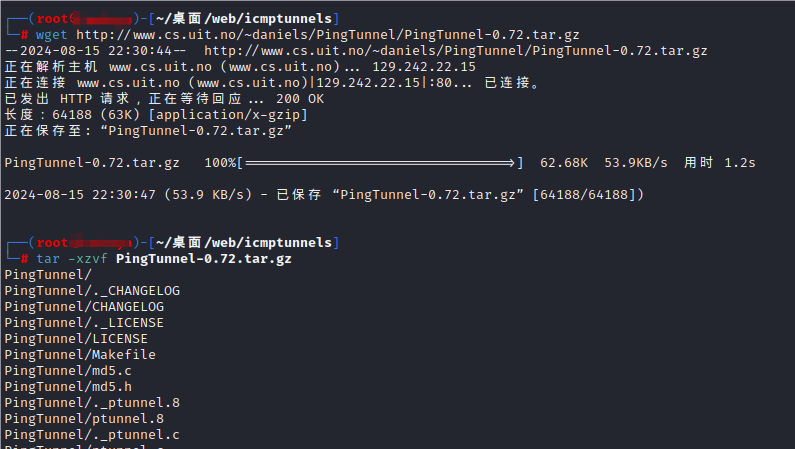
8月15日笔记
masscan安装使用 首先需要有c编译器环境。查看是否有c编译器环境: gcc -v如果系统中已经安装了 GCC,这个命令将输出 GCC 的版本信息。如果未安装,你会看到类似于 “command not found” 的错误消息。 如果没有下载,使用如下命令…...

CSS3 圆角
CSS3 圆角 引言 在网页设计中,圆角矩形是一种常见的设计元素,它们为页面带来了柔和的视觉体验。随着CSS3的推出,实现圆角矩形变得异常简单,无需依赖图片或复杂的JavaScript代码。本文将详细介绍CSS3中用于创建圆角矩形的border-…...

VUE项目中main.js中不能使用 @引入路径吗
VUE项目中main.js中不能使用 引入路径吗 vite.config已经配置了别名 但是在main.js中直接引入报错 修改成 相对路径后,保存消失 找到原因:vite.config 漏了引入 import { defineConfig } from ‘vite’ import vue from ‘vitejs/plugin-vue’ 导致…...

Spring日志
1.日志的作用 定位和发现问题(主要)系统监控数据采集日志审计...... 2.日志的使用 2.1 ⽇志格式的说明 2.2 打印日志 Spring集成了日志框架,直接使用即可 步骤: 1.定义日志对象 2.使⽤⽇志对象打印⽇志 RestController public class LoggerController {private static Logger…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
