Python|蓝桥杯进阶第五卷——数论

欢迎交流学习~~
专栏: 蓝桥杯Python组刷题日寄
蓝桥杯进阶系列:
🏆 Python | 蓝桥杯进阶第一卷——字符串
🔎 Python | 蓝桥杯进阶第二卷——贪心
💝 Python | 蓝桥杯进阶第三卷——动态规划
✈️ Python | 蓝桥杯进阶第四卷——图论
🌞 Python | 蓝桥杯进阶第五卷——数论
💎 Python | 蓝桥杯进阶第六卷——搜索
Python|蓝桥杯进阶第五卷——数论
- 🎁 买不到的数目
- 🌲 幂方分解
- 💡 麦森数
- 🍞 欧拉函数
🎁 买不到的数目
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
小明开了一家糖果店。他别出心裁:把水果糖包成 4 颗一包和 7 颗一包的两种。糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是17。大于17的任何数字都可以用 4 和 7 组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入描述:
两个正整数,表示每种包装中糖的颗数(都不多于1000)
输出描述:
一个正整数,表示最大不能买到的糖数
样例输入:
4 7
样例输出:
17
解题思路
这里需要先确定上边界,然后针对小于其的数逐个判断即可。(代码1)
借助数论中的结论:自然数 a,ba,ba,b 互质,则不能表示成 ax+byax+byax+by(x,yx,yx,y 为非负整数)的最大整数是 ab−a−bab-a-bab−a−b,本题中所给出的数据全部为质数,因此可以使用。(代码2)
参考代码
# 代码1
from math import gcd
def check(a, b, n):if n%a == 0 or n%b == 0:return Truex = n//amod = n%afor i in range(x+1):if (i*a+mod)%b == 0:return Truereturn Falsedef func(a, b):# 计算上边界,这里取最小公倍数max_num = (a*b)//gcd(a, b)for i in range(max_num-1, 0, -1):if not check(a, b, i):print(i)breaka, b = map(int, input().split())
func(a, b)
# 代码2
n,m = map(int, input().strip().split())
print(n*m-m-n)
🌲 幂方分解
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
任何一个正整数都可以用 2 的幂次方表示。例如:
137=2^7+2^3+2^0
同时约定方次用括号来表示,即 ab 可表示为 a(b)。
由此可知,137 可表示为:
2(7)+2(3)+2(0)
进一步:7= 2^2+2+2^0 (2^1 用 2 表示)
3=2+2^0
所以最后 137 可表示为:
2(2(2)+2+2(0))+2(2+2(0))+2(0)
又如:
1315=2^10+2^8+2^5+2+2^0
所以 1315 最后可表示为:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
输入描述:
输入包含一个正整数 N(N<=20000),为要求分解的整数。
输出描述:
程序输出包含一行字符串,为符合约定的 n 的 0,2 表示(在表示中不能有空格)
样例输入:
1315
样例输出:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)
解题思路
可以通过每个数的二进制来得到其二次幂分解:
比如样例中的 1315,其对应的二进制数为:0b10100100011
其中 1 对应的位置由高到低为:11 9 6 2 1
因此其对应二次幂分解为:1315 = 2^10 + 2^8 + 2^5 +2 ^1 + 2^0
对于 0 次幂和 1 次幂特别处理,而对于高次幂,通过递归调用。
注意:要从高次幂开始处理。
具体见参考代码及其注释。
参考代码
def trans(n):# 转为 2 进制后再处理tmp = list(bin(n))# 去除 2 进制前面的 0bn = tmp[2:]# 转换为整数n = [int(i) for i in n]res = ''for i in range(1, len(n) + 1):if n[len(n) - i]:if len(n) - i == 0:# 处理 0 次幂res += '2(0)+'elif len(n) - i == 1:# 处理 1 次幂res += '2+'else:# 其余情况,递归调用res += '2(' + trans(len(n) - i) + ')+'# 最后res会有一个 '+' 需要去除return res[:-1]if __name__ == '__main__':n = int(input())print(trans(n))
💡 麦森数
题目:
时间限制:
3s
内存限制:
192MB
题目描述:
形如 2^p-1 的素数称为麦森数,这时 p 一定也是个素数。但反过来不一定,即如果 p 是个素数,2^p-1不一定也是素数。到1998年底,人们已找到了 37 个麦森数。最大的一个是p=3021377,它有 909526 位。麦森数有许多重要应用,它与完全数密切相关。
任务:从文件中输入 p(1000 < p < 3100000),计算 2^p-1 的位数和最后 500 位数字(用十进制高精度数表示)
输入描述:
文件中只包含一个整数 p(1000 < p < 3100000)
输出描述:
第一行:十进制高精度数 2^p-1的位数。
第2-11行:十进制高精度数 2^p-1 的最后 500 位数字。(每行输出 50 位,共输出 10 行,不足 500 位时高位补 0)
不必验证 2^p-1 与 p 是否为素数。
样例输入:
1279
样例输出:
386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087 解题思路
对于一个十进制数 k,其位数 A 为:A = int(log10(k) + 1)
因为当 p 取较大值时,整个数过大,考虑到最后只需要输出 500 位,我们将其对 10**500 取幂,之后再按照要求格式输出。
具体见参考代码和注释。
参考代码
from math import log10 as lg
p = int(input())
print(int(p * lg(2)) + 1)num = 2**p - 1
# 预处理,因为最后只需要500位,对 10**500 取幂
num = num % (10**500)
res = []
# 计算结果
for i in range(500):res.append(num % 10)num //= 10# 按照要求打印
for i in range(499, -1, -1):print(res[i], end='')if i % 50 == 0:print('')
🍞 欧拉函数
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
给定一个大于 1,不超过 2000000 的正整数 n,输出欧拉函数,phi(n) 的值。
如果你并不了解欧拉函数,那么请参阅提示。
提示:
欧拉函数 phi(n) 是数论中非常重要的一个函数,其表示 1 到 n-1 之间,与 n 互质的数的个数。显然的,我们可以通过定义直接计算 phi(n)。
当然,phi(n) 还有这么一种计算方法。
首先我们对 n 进行质因数分解,不妨设 n=p1^a1 * p2^a2 * ... * pk^ak (这里 a^b 表示 a 的 b次幂,p1 到 pk 为 k 个互不相同的质数,a1 到 ak 均为正整数),那么
phi(n)=n(1-(1/p1))(1-(1/p2))....(1-(1/pk))
稍稍化简一下就是
phi(n)=n(p1-1)(p2-1)...(pk-1)/(p1*p2*...*pk)
计算的时候小心中间计算结果超过 int 类型上界,可通过调整公式各项的计算顺序避免(比如先做除法)!
输入描述:
在给定的输入文件中进行读入:
一行一个正整数 n。 不超过 2000000 的正整数 n.
输出描述:
将输出信息输出到指定的文件中:
一行一个整数表示 phi(n)。
样例输入:
17
样例输出:
16
解题思路
直接按照定义来写即可
参考代码
from math import gcd
n = int(input())
count = 0
for i in range(1,n):if gcd(i,n)==1:count += 1
print(count)
相关文章:

Python|蓝桥杯进阶第五卷——数论
欢迎交流学习~~ 专栏: 蓝桥杯Python组刷题日寄 蓝桥杯进阶系列: 🏆 Python | 蓝桥杯进阶第一卷——字符串 🔎 Python | 蓝桥杯进阶第二卷——贪心 💝 Python | 蓝桥杯进阶第三卷——动态规划 ✈️ Python | 蓝桥杯进阶…...

用Python实现单例模式
什么是单例模式单例模式是指在内存中只会创建且仅创建一次对象的设计模式。在程序中多次使用同一个对象且作用相同时,为了防止频繁地创建对象使得内存飙升,单例模式可以让程序仅在内存中创建一个对象,让所有需要调用的地方都共享这一单例对象…...

交叉编译说明:工具链安装和环境变量配置
目录 一 简单了解交叉编译 ① 什么是交叉编译 ② 为什么需要交叉编译 ③ 宿主机和目标机 二 搭建交叉编译工作环境 ① 安装工具链 ② 配置环境变量 ● 配置临时环境变量 ● 配置永久环境变量 三 交叉编译宿主机和目标机 ● 宿主机编译生成的可执行文件下载到目…...
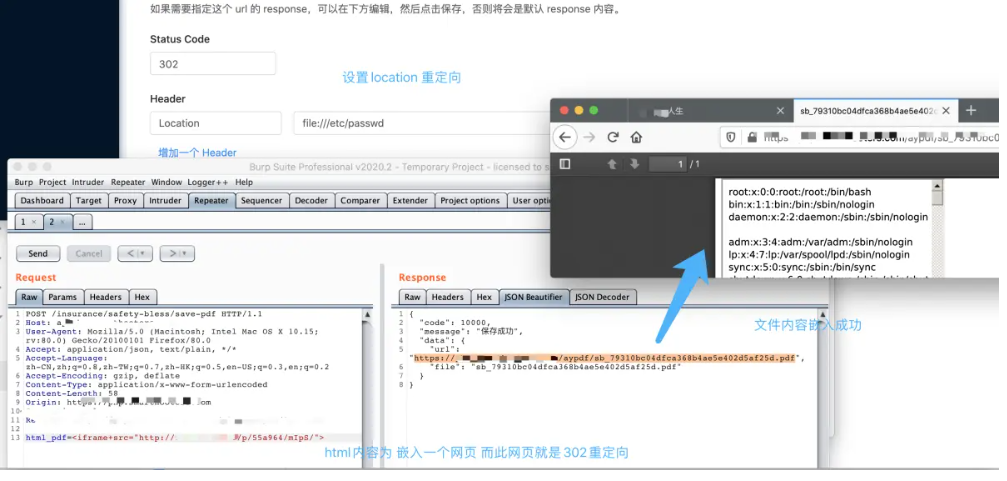
文件上传的多种利用方式
文件上传的多种利用方式 文件上传漏洞除了可以通过绕过检测进行webshell的上传之外,还有多种其它的漏洞可以进行测试。 XSS漏洞 文件名造成的XSS 当上传任何文件时,文件名肯定是会反显示在网页上,可以使用 XSS Payload做文件名尝试将其上传到…...
)
盘一盘C++的类型描述符(二)
先序文章请看 盘一盘C的类型描述符(一) 稍微组合一下的复杂类型 数组指针类型的数组类型 数组的指针类型我们已经了解了,那么,以这种类型作为元素的数组类型怎么搞? using type int (*)[3]; // 元素类型是数组指针…...

慎投,Frontiers这本期刊显示on hold中
什么是“On Hold”? 该期刊因为质量问题正在被进行重新评估;在重新评估过程中,不会检索新发表的文章。该期刊因为质量问题正在被进行重新评估;在重新评估过程中,不会检索新发表的文章。根据选择标准,在最严…...
——ProgressBar(史上最全))
Winform控件开发(21)——ProgressBar(史上最全)
一、属性 1、Name 用于获取控件对象 2、Anchor 锚定控件对于父控件的位置 3、BackColor 背景色 4、ContextMenuStrip 关联的上下文菜单 5、Cursor 鼠标移动到控件上显示的光标 6、Dock 停靠在父控件的位置 7、Enabled 是否启动该控件,false时事件都不能触发 8、…...

校招失败后,在外包公司熬了 2 年终于进了字节跳动,竭尽全力....
其实两年前校招的时候就往字节投了一次简历,结果很明显凉了,随后这个理想就被暂时放下了,但是这个种子一直埋在心里这两年除了工作以外,也会坚持写博客,也因此结识了很多优秀的小伙伴,从他们身上学到了特别…...
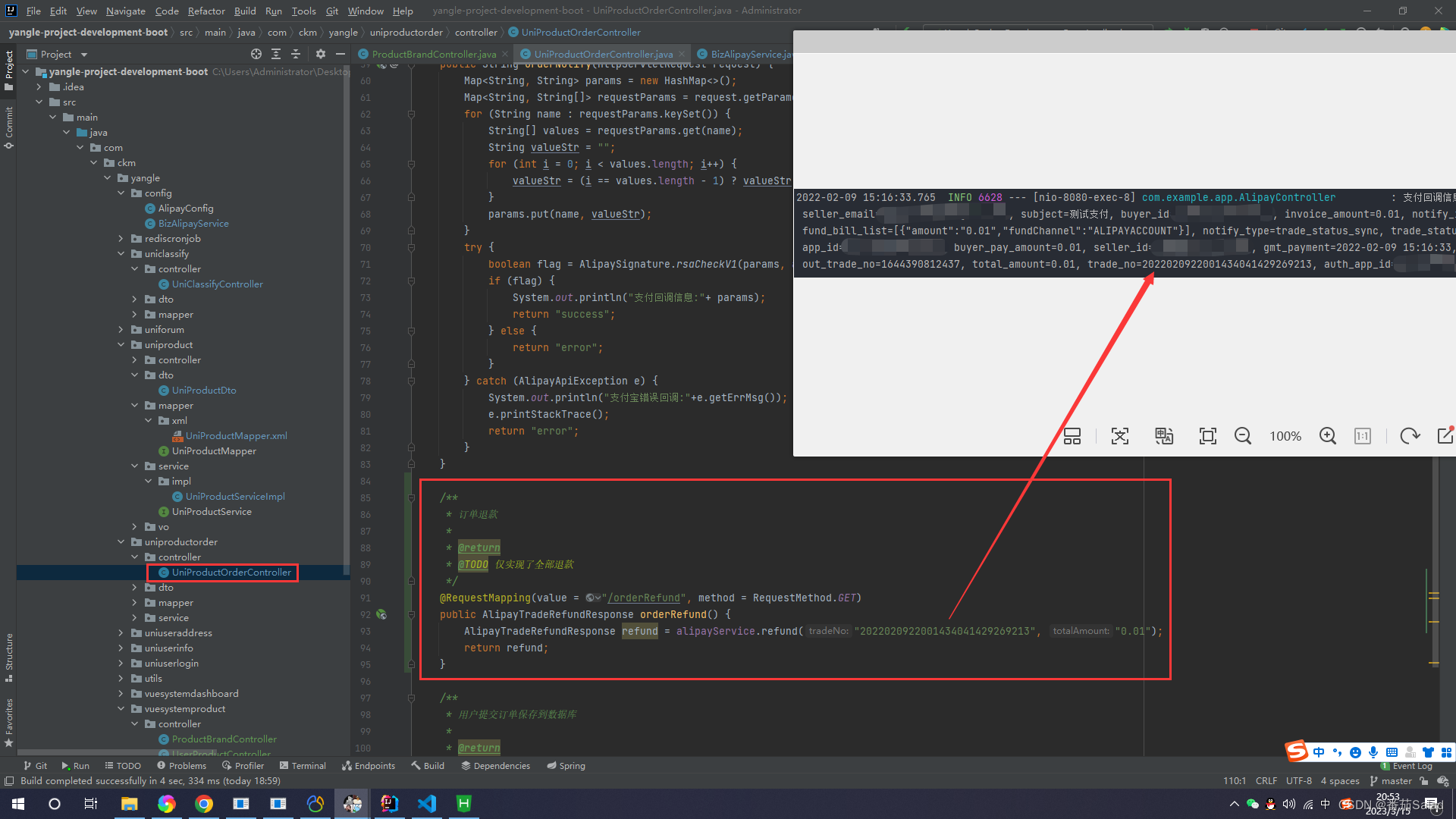
UniApp + SpringBoot 实现接入支付宝支付功能和退款功能
一、支付宝开放平台设置 注册支付宝支付功能需要个体工商户或企业才可以!需要有营业执照才能去申请哦! 1、登录到控制台 进入支付宝开放平台 控制台 2、开发设置 3、产品绑定APP支付 如果没有绑定APP支付就会报商家订单参数异常,请重新发起…...
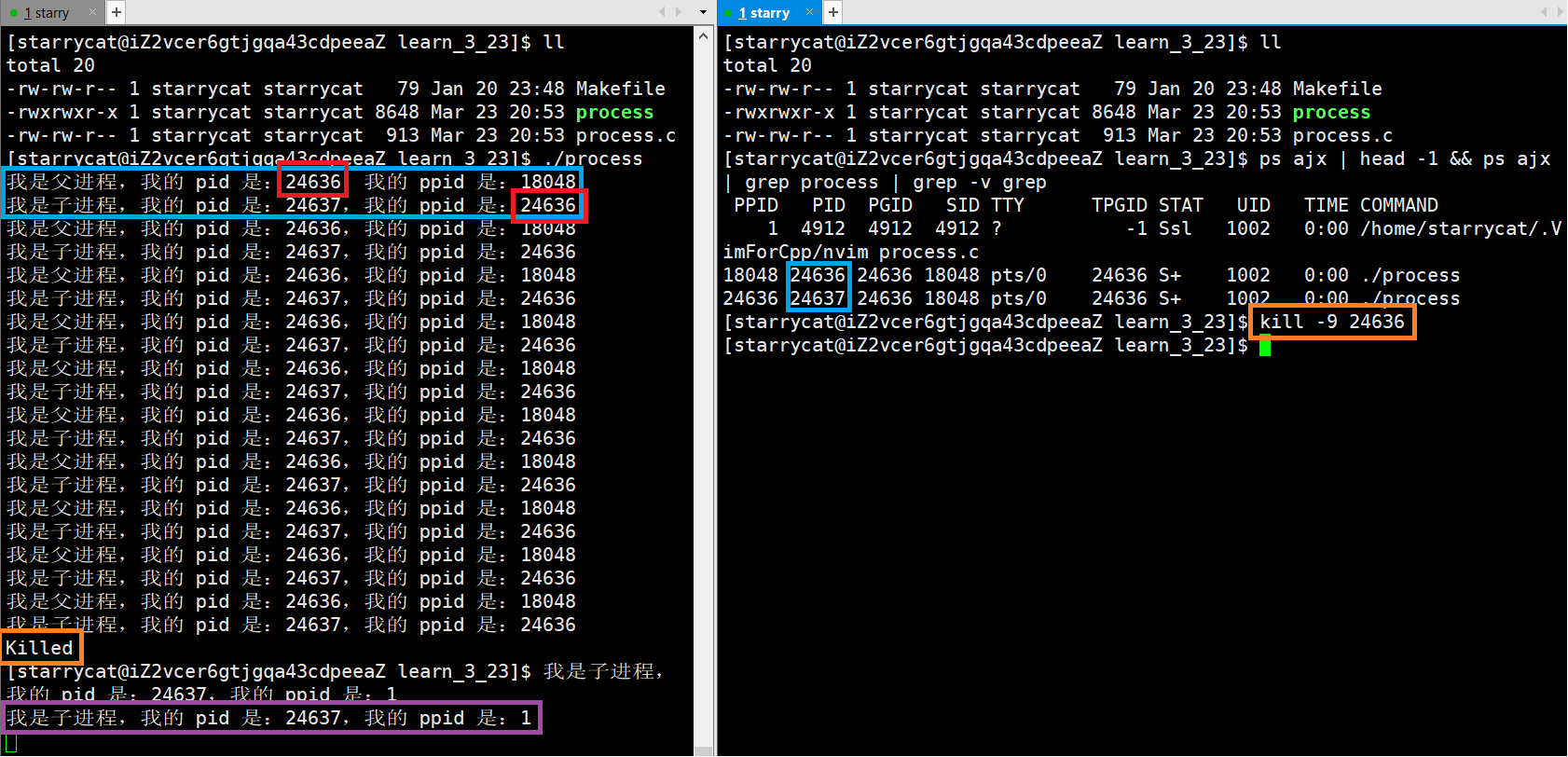
初识进程
文章目录一、进程的概念1. 进程是什么及进程的管理2. Linux 下的 pcb3. 系统调用接口 getpid 和 getppid4. 系统调用接口 fork一、进程的概念 1. 进程是什么及进程的管理 在 Linux下 ./binaryfile 运行一个程序或者在 Windows下双击运行一个程序时,程序就变成了一个…...
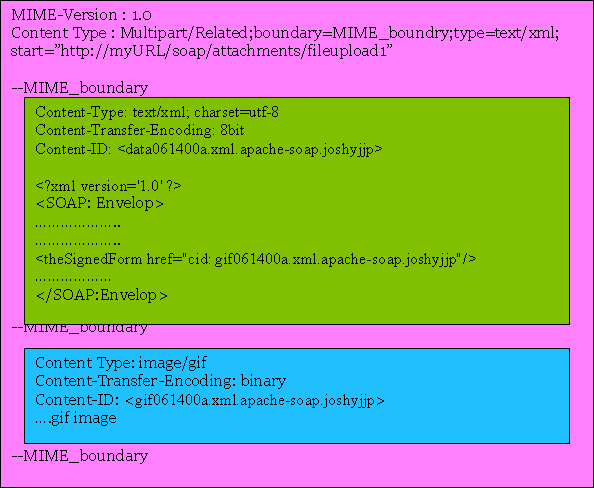
SOAP传输协议
一.HTTP传输协议 超文本传输协议(HyperText Transfer Protocol,缩写:HTTP),它是基于请求-响应的模式协议,客户端发出请求,服务器端给出响应并返回请求内容。方法如下,HTTP传输协议常…...
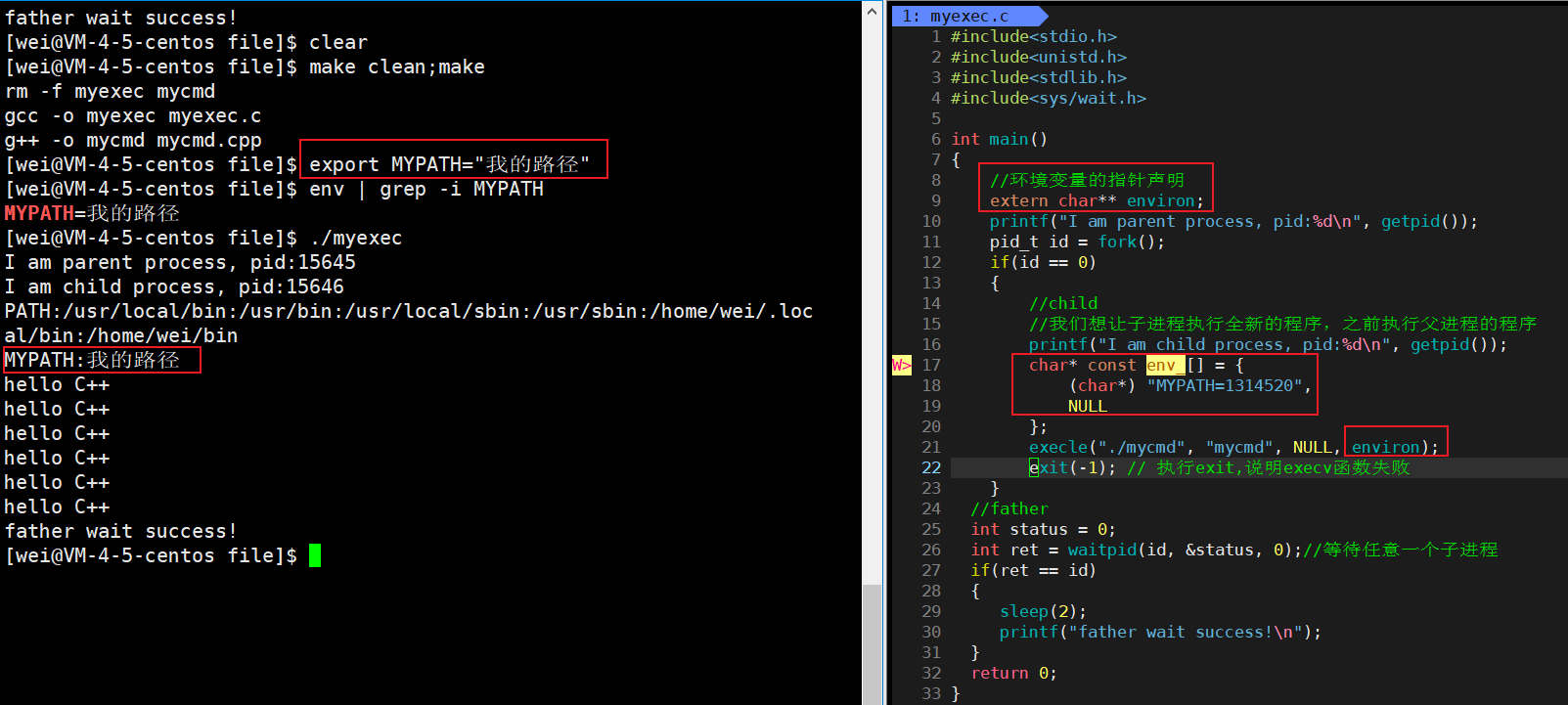
<Linux>进程控制
进程控制 文章目录进程控制一、进程创建1.fork函数认识2.写时拷贝3.fork常规用法4.fork调用失败的原因二、进程终止1.进程退出场景2.进程退出码3.进程退出的方式三、进程等待1.进程等待是什么?2.进程等待的必要性3.进程等待的方法3.1.wait函数3.2.waitpid函数4.如何…...

有手就行 -- 搭建图床(PicGo+腾讯云)
🍳作者:贤蛋大眼萌,一名很普通但不想普通的程序媛\color{#FF0000}{贤蛋 大眼萌 ,一名很普通但不想普通的程序媛}贤蛋大眼萌,一名很普通但不想普通的程序媛🤳 🙊语录:多一些不为什么的…...
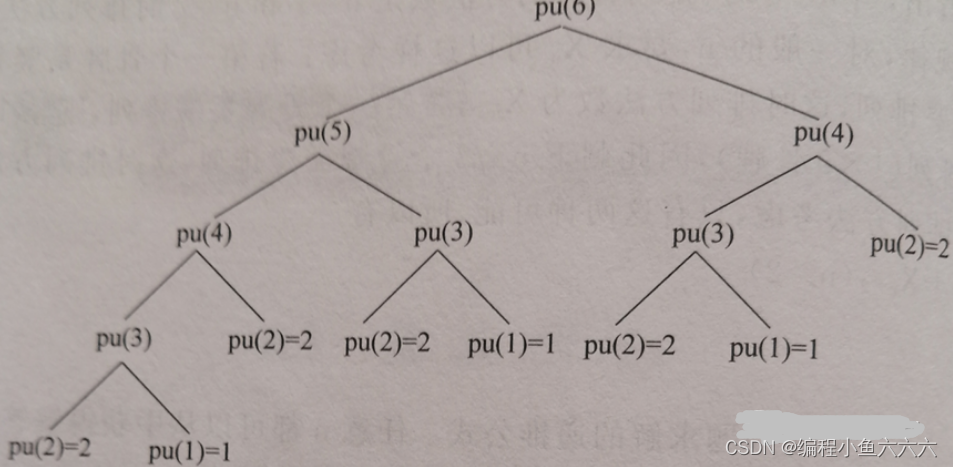
“蓝桥杯”递推和递归(一)——取数位
1. 算法简介 递推和递归虽然叫法不同,但它们的基本思想是一致的,在很多程序中,这两种算法可以通用,不同的是递推法效率更高,递归法更方便阅读。 (1)递推法 递推法是一种重要的数学方法&#…...

蓝桥杯·3月份刷题集训Day02
本篇博客旨在记录自已打卡蓝桥杯3月份刷题集训,同时会有自己的思路及代码解答希望可以给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉💪。 文…...

python --获取内网IP地址
方法一 import socketdef get_local_ip_address():ip_address try:# 获取本机主机名hostname socket.gethostname()# 获取本机IPip_address socket.gethostbyname(hostname)except:passreturn ip_address方法二 import subprocessdef get_local_ip_address():ip_address …...

如何衡量你的Facebook广告活动的成功
投入大量资金和资源在Facebook广告上并不总能带来预期的回报,这很可能是由于缺乏恰当的衡量广告活动成功的方法。在这篇文章中,我们将介绍一些关键的指标,帮助你更好地了解如何衡量你的Facebook广告活动的成功。1.费用每次点击(CP…...

Linux对一个目录及其子目录所有文件添加权限
1、chmod指令 chmod是一个改变用户拥有指定文件的权限的命令.r:只读,w:写,x执行.也可以用数字 -rw------- (600) -- 只有属主有读写权限。 -rw-r--r-- (644) -- 只有属主有读写权限;而属组用户和其他用户只有读权限。 -rwx------ (700) -- 只有属主有读、写、执…...

宝刀未老?低代码何德何能受大厂们的推崇
风口之下,低代码蓬勃发展,本文从国内低代码的走红现象引入,浅析低代码发展中的变化趋势,重点探讨如此趋势之下,国内大厂如何通过低代码实现了良性发展。 一、国内爆火的低代码 据Gartner最新报告显示,到2…...
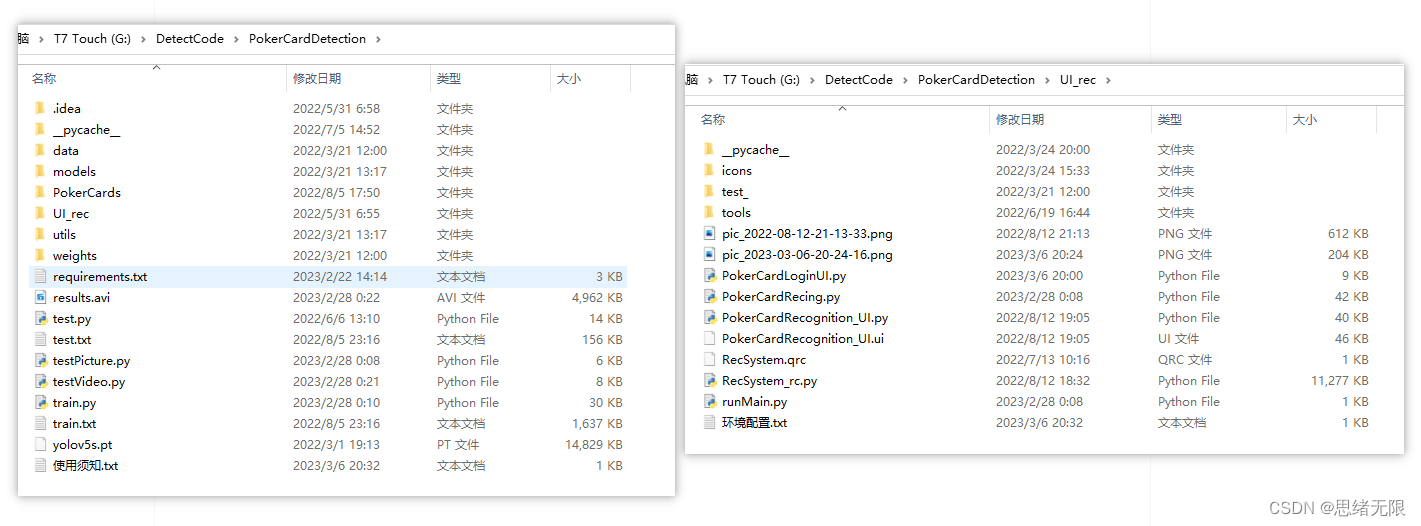
智能扑克牌识别软件(Python+YOLOv5深度学习模型+清新界面)
摘要:智能扑克牌识别软件利用视觉方法检测和识别日常扑克牌具体花色与数字,快速识别牌型并标注结果,帮助计算机完成扑克牌对战的前期识别步骤。本文详细介绍基于深度学习的智能扑克牌识别软件,在介绍算法原理的同时,给…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
