Week 14
代码源每日一题Div2
106. 订单编号
原题链接:订单编号
思路:这题本来没啥思路,直到获得了某位佬的提示才会做(
我们可以用set来维护一些区间,这些区间为 pair 类型,表示没有使用过的编号,每次我们只需要用set容器中的lower_bound函数来找到一个上界大于等于该编号的区间,于是就容易看出新的编号为该区间的下界和原编号的较大值。获得新编号后我们需要将此时的区间进行分割,以新编号为中点将区间分为左右两块,表示新的两个其中的编号没有使用过的区间。重复此操作即可解决这道题。
代码:
#include <bits/stdc++.h>
using namespace std;
int n, a[500005];
set<pair<int, int> > s;
int main(){cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];}s.insert(make_pair(2e9, 1));for(int i = 1; i <= n; i++){auto it = s.lower_bound({a[i], 0});int l = it->second, r = it->first;int num = max(l, a[i]);if(num + 1 <= r) s.insert({r, num + 1});if(num - 1 >= l) s.insert({num - 1, l});s.erase(it);cout << num << " ";}return 0;
}
107. 饿饿 饭饭
原题链接:饿饿 饭饭
思路:设给当前的所有人都打一次饭为一轮,则我们可以用二分来找到一共需要多少轮才能把 k 次饭全部打完。找到总轮数后再用队列模拟最后一轮的情况即可。
代码:
#include <bits/stdc++.h>
using namespace std;
long long n, k, a[100005], sum, res;
queue<long long> q;
int main(){cin >> n >> k;for(int i = 1; i <= n; i++){cin >> a[i];sum += a[i];}if(sum < k){cout << -1 << endl;return 0;}int st = 0, ed = 1e9;while(st <= ed){sum = 0;long long mid = (st + ed) / 2;for(int i = 1; i <= n; i++){sum += min(a[i], mid);}if(sum >= k) ed = mid - 1;else st = mid + 1, res = mid;}sum = 0;for(int i = 1; i <= n; i++){sum += min(a[i], res);a[i] = max(a[i] - res, (long long)0);if(a[i] > 0) q.push(i);}k -= sum;for(int i = 0; i < k; i++){if(a[q.front()] == 1) q.pop();else{q.push(q.front());a[q.front()] -= 1;q.pop();}}while(!q.empty()){cout << q.front() << " ";q.pop();}return 0;
}
204. 加一
原题链接:加一
思路:可以利用动态规划来先对数字加一后的长度进行预处理,设 dp[i][j] 为数字 j 经过·i 次加一操作后的长度,则状态转移方程为
dp[i + 1][j - 1] = dp[i][j], 1<= j <= 9
由于 9 进行加一后会变为10, 因此此时的长度为 0 和 1 上一次操作后的长度之和, 因此状态转移方程为
dp[i + 1][9]=(dp[i][0] + dp[i][1]) % (int)(1e9 + 7)
预处理后一次读入每一位数字并将结果相加即可
代码:
#include<bits/stdc++.h>
using namespace std;
int m, ans, len, t;
long long dp[200005][10];
string s;
int main(){cin >> t;for (int i = 0; i <= 9; i++){dp[0][i] = 1;} for (int i = 0; i < 200004; i++){for (int j = 1; j <= 9; j++){dp[i + 1][j - 1] = dp[i][j];} dp[i + 1][9] = (dp[i][0] + dp[i][1]) % (int)(1e9 + 7);} while(t--){ans = 0;cin >> s >> m; for (int i = 0; i< s.size(); i++){ans = (ans + dp[m][s[i]-'0']) % (int)(1e9 + 7);} printf("%d\n", ans);} return 0;
}
205. 跳跳
原题链接:跳跳
思路:由题意,一种魔法代表一组点之间连线的斜率,因此遍历所有点并算出每两点间的斜率,并将算出的斜率存入set容器来避免重复,最终set容器中元素的数量 * 2 即为最终答案。
为什么要乘二?因为传送是有方向的,点1传送到点2与点2传送到点1是两种不同情况
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
struct point{double x, y;
} p[505];
set<double> k;
int main(){cin >> n;for(int i = 1; i <= n; i++){cin >> p[i].x >> p[i].y;} for(int i = 1; i <= n; i++){for(int j = 1; j < i; j++){double tmp = (p[i].y - p[j].y) / (p[i].x - p[j].x);k.insert(tmp);}}cout << k.size() * 2;return 0;
}
206. 异或和或
原题链接:异或和或
思路:通关观察题目要求,我们可以找到这样的规律:
(0, 0) -> (0, 0)
(0, 1) / (1, 0) -> (1, 1) -> (1, 0) / (0, 1)
(1, 1) -> (0, 1)
因此,在一个序列中,在变化某一位的数字时只要在此序列中的其他位置存在数字 1 则那一位的数字就一定可以变成与下一个序列相应位置一样的数字。又由上述规律,(0,1)与(1,0)可以随意转换,因此当两个序列有相同数量的 1 时,一定可以将两序列变换为一样的。
代码:
#include <bits/stdc++.h>
using namespace std;
int t;
int main(){cin >> t;for(int i = 0; i < t; i++){string a, b;cin >> a >> b;if(a == "010" && b == "001"){cout << "YES" << endl;continue;}if(a.size() != b.size()){cout << "NO" << endl;continue;} for(int j = 0; j < a.size(); j++){bool flag = false;if(a[j] != b[j]){for(int k = 0; k < a.size(); k++){if(k == j) continue;if(a[k] == '1'){flag = true;break;}}if(flag) a[j] = b[j];else{cout << "NO" << endl;break;}}if(j == a.size() - 1 && a == b) cout << "YES" << endl;}}return 0;
}
207. 01序列
原题链接:01序列
思路:通过观察可以发现,当一个满足条件的子串的两端均为1时,此时若加入子串左边的0序列则加入0后的子串依然能满足条件,且每加入一个0满足条件的子串数量都能增加1个,同时,此时若向右加入0序列,则每次增加的满足条件的子串数量为左边加入0后满足条件的子串的总数。由此规律即可解决该问题。
代码:
#include <bits/stdc++.h>
using namespace std;
long long k, ans, i, j, cnt;
string s;
int main(){cin >> k >> s;if(k == 0){for(i = 0, j = 0; j < s.size(); i++, j++){while(j < s.size() && s[j] == '1') j++;i = j;while(j < s.size() && s[j] == '0') j++;ans += (j - i) * (j - i + 1) / 2;}cout << ans;return 0;}for(i = 0, j = 0; j < s.size(); i++, j++){while(j < s.size()){if(s[j] == '1') cnt++;if(cnt == k) break;j++;}if(cnt == k){int r = j + 1;while(r < s.size() && s[r] == '0'){r++;}while(i < s.size() && s[i] == '0'){ans += r - j;i++;}ans += r - j;cnt--;}}cout << ans;return 0;
}
301. 出栈序列判断
原题链接:出栈序列判断
思路:由于数字升序入栈,那么数字正常出栈时一定是降序排列,因此如果输出的序列中出现了升序的数字,那么此时就需要把出现升序的第一个数字立刻pop出去。由此规律就可以写代码了。
代码:
#include <bits/stdc++.h>
using namespace std;
int n, a[100005], cnt1 = 1, cnt2 = 1;
int read(){int f=1,k=0;char c=getchar();while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar(); }while(c>='0'&&c<='9'){k=k*10+c-'0';c=getchar(); }return f*k;
}
int main(){n = read();for(int i = 1; i <= n; i++){a[i] = read();}for(int i = 1, j = 2; j <= n; j++){if(a[j] > a[i]){for(int k = cnt1; k <= a[i]; k++){printf("push %d\n", k);cnt1++;}for(int k = 1; k <= j - i; k++){printf("pop\n");cnt2++;}i = j;}}for(int k = cnt1; k <= n; k++){printf("push %d\n", k);}for(int k = cnt2; k <= n; k++){printf("pop\n");}return 0;
}
302. 序列维护
原题链接:序列维护
思路:简单模拟插入和删除数组元素的过程即可。
代码:
#include <bits/stdc++.h>
using namespace std;
int m, a[1005], len;
string s;
int main(){cin >> m;for(int i = 0; i < m; i++){cin >> s;if(s == "insert"){int x, y;cin >> x >> y;for(int j = len - 1; j >= x; j--){a[j + 1] = a[j];}a[x] = y;len++;}else if(s == "query"){int k;cin >> k;cout << a[k - 1] << endl;}else{int x;cin >> x;for(int j = x; j < len; j++){a[j - 1] = a[j];}len--;}}return 0;
}
303. 网格判断
原题链接:网格判断
思路:直接遍历每一行和每一列,依照题意对其中的字符进行判断即可。
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
char mp[30][30];
bool checkCount(){for(int i = 1; i <= n; i++){int cntw = 0, cntb = 0;for(int j = 1; j <= n; j++){if(mp[i][j] == 'W') cntw++;else if(mp[i][j] == 'B') cntb++;} if(cntw != cntb) return false;}for(int i = 1; i <= n; i++){int cntw = 0, cntb = 0;for(int j = 1; j <= n; j++){if(mp[j][i] == 'W') cntw++;else if(mp[j][i] == 'B') cntb++;}if(cntw != cntb) return false;}return true;
}
bool checkContinue(){for(int i = 1; i <= n; i++){for(int j = 1; j <= n - 2; j++){if(mp[i][j] == mp[i][j + 1] && mp[i][j + 1] == mp[i][j + 2]) return false;}}for(int i = 1; i <= n; i++){for(int j = 1; j <= n - 2; j++){if(mp[j][i] == mp[j + 1][i] && mp[j + 1][i] == mp[j + 2][i]) return false;}}return true;
}
int main(){cin >> n;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cin >> mp[i][j];}}if(checkCount() && checkContinue()) cout << 1;else cout << 0;return 0;
}
304. 整齐的数组
原题链接:整齐的数组
思路:遍历数组中的所有元素,找到每一个元素的差的绝对值,并求出这些差的最大公因数即可。
代码:
#include <bits/stdc++.h>
using namespace std;
int t, a[50], n;
int main(){cin >> t;for(int i = 0; i < t; i++){cin >> n;for(int j = 1; j <= n; j++){cin >> a[j];}int ans = 0;for(int j = 1; j <= n; j++){for(int k = 1; k < j; k++){int tmp = fabs(a[j] - a[k]);ans = ans == 0 ? tmp : __gcd(ans, tmp);}}if(ans != 0) cout << ans << endl;else cout << -1;}return 0;
}
相关文章:

Week 14
代码源每日一题Div2 106. 订单编号 原题链接:订单编号 思路:这题本来没啥思路,直到获得了某位佬的提示才会做( 我们可以用set来维护一些区间,这些区间为 pair 类型,表示没有使用过的编号,每次…...

【微信小程序】-- 使用 Git 管理项目(五十)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

leetcode每日一题:134. 加油站
系列:贪心算法 语言:java 题目来源:Leetcode134. 加油站 题目 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[…...

开放式基金实时排行 API 数据接口
开放式基金实时排行 API 数据接口 多维度参数返回,实时数据,类型参数筛选。 1. 产品功能 返回实时开放式基金排行数据可定义查询基金类型参数;多个基金属性值返回多维指标,一次查询毫秒级返回;数据持续更新与维护&am…...

Android开发中synchronized的实现原理
synchronized的三种使用方式 **1.修饰实例方法,**作用于当前实例加锁,进入同步代码前要获得当前实例的锁。 没有问题的写法: public class AccountingSync implements Runnable{//共享资源(临界资源)static int i0;/*** synchronized 修饰实例方法*/p…...
)
【华为OD机试 2023最新 】 统一限载货物数最小值(C++)
题目描述 火车站附近的货物中转站负责将到站货物运往仓库,小明在中转站负责调度2K辆中转车(K辆干货中转车,K辆湿货中转车)。 货物由不同供货商从各地发来,各地的货物是依次进站,然后小明按照卸货顺序依次装货到中转车,一个供货商的货只能装到一辆车上,不能拆装,但是…...
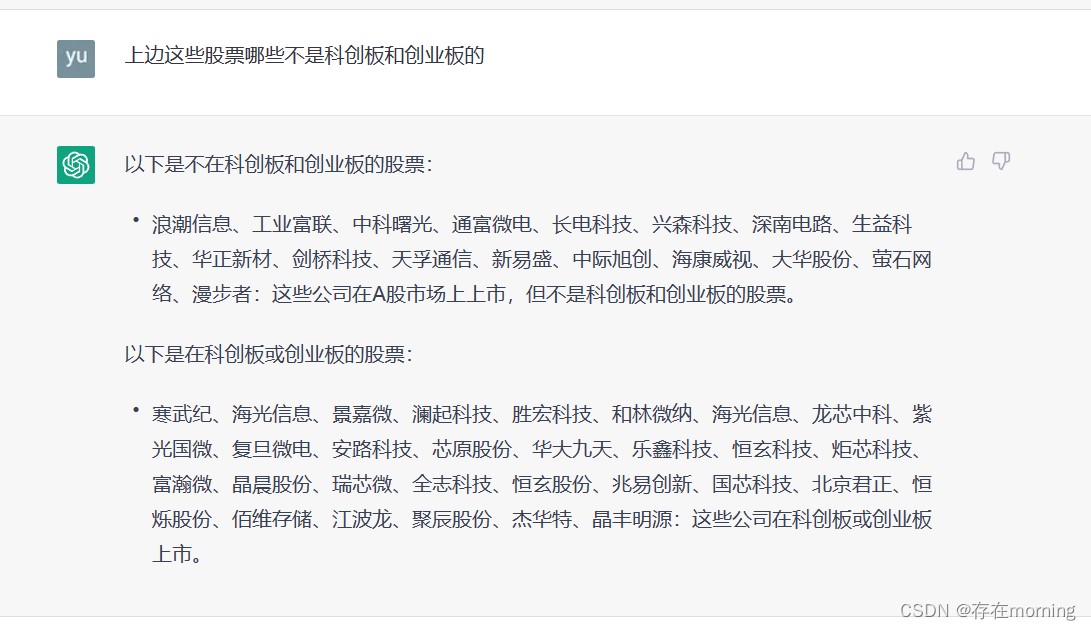
【生活工作经验 十】ChatGPT模型对话初探
最近探索了下全球大火的ChatGPT,想对此做个初步了解 一篇博客 当今社会,自然语言处理技术得到了迅速的发展,人工智能技术也越来越受到关注。其中,基于深度学习的大型语言模型,如GPT(Generative Pre-train…...

基于Spring Boot房产销售平台的设计与实现【源码+论文】分享
开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 摘要 信息技术的发展…...

不同类型的电机的工作原理和控制方法汇总
电机控制是指对电机的启动、调速(加速、减速)、运转方向和停止进行的控制,不同类型的电机有着不同的工作原理和控制方法。 一、无刷电机 无刷电机是由电机主体和电机驱动板组成的一种没有电刷和换向器的机电一体化产品。在无刷电机中…...

计算机网络管理 TCP三次握手的建立过程,Wireshark抓包分析并验证TCP三次握手建立连接的报文
⬜⬜⬜ ---🟧🟨🟩🟦🟪 (*^▽^*)欢迎光临 🟧🟨🟩🟦🟪---⬜⬜⬜ ✏️write in front✏️ 📝个人主页:陈丹宇jmu 🎁欢迎各位→…...
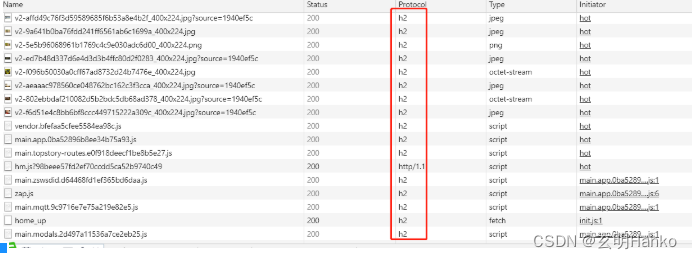
HTTP/2.x:最新的网页加载技术,快速提高您的SEO排名
2.1 http2概念HTTP/2.0(又称HTTP2)是HTTP协议的第二个版本。它是对HTTP/1.x的更新,旨在提高网络性能和安全性。HTTP/2.0是由互联网工程任务组(IETF)标准化的,并于2015年发布。2.2 http2.x与http1.x区别HTTP…...

机器学习----线性回归
第一关:简单线性回归与多元线性回归 1、下面属于多元线性回归的是? A、 求得正方形面积与对角线之间的关系。 B、 建立股票价格与成交量、换手率等因素之间的线性关系。 C、 建立西瓜价格与西瓜大小、西瓜产地、甜度等因素之间的线性关系。 D、 建立西瓜…...
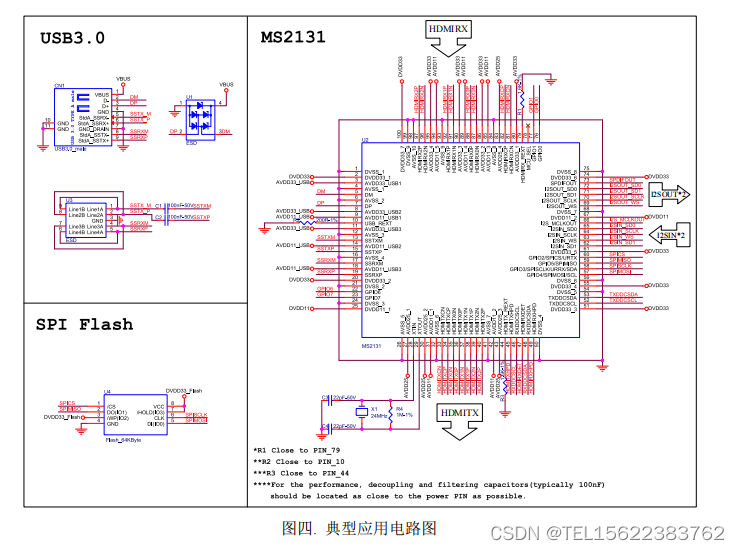
MS2131 USB 3.0 高清音视频采集+HDMI 环出+混音处理芯片 应用网络直播一体机
MS2131 是一款 USB 3.0 高清视频和音频采集处理芯片,内部集成 USB 3.0 Device 控制器、 数据收发模块、音视频处理模块。MS2131 可以通过 USB 3.0 接口将 HDMI 输入的音视频信号传 送到 PC、智能手机、平板电脑上预览或采集。MS2131 支持 HDMI 环出功能,…...

基于堆与AdjustDown的TOP-K问题
TIPSTOP-K问题TOP-K问题:就是说现在比如说有n个数据,然后需要从这n个数据里面找到最大的或最小的前k个。一般来讲思路的话就是:先把这n个数据给他建一个堆,建堆完成之后,然后就去调堆,然后大概只需要调k次&…...
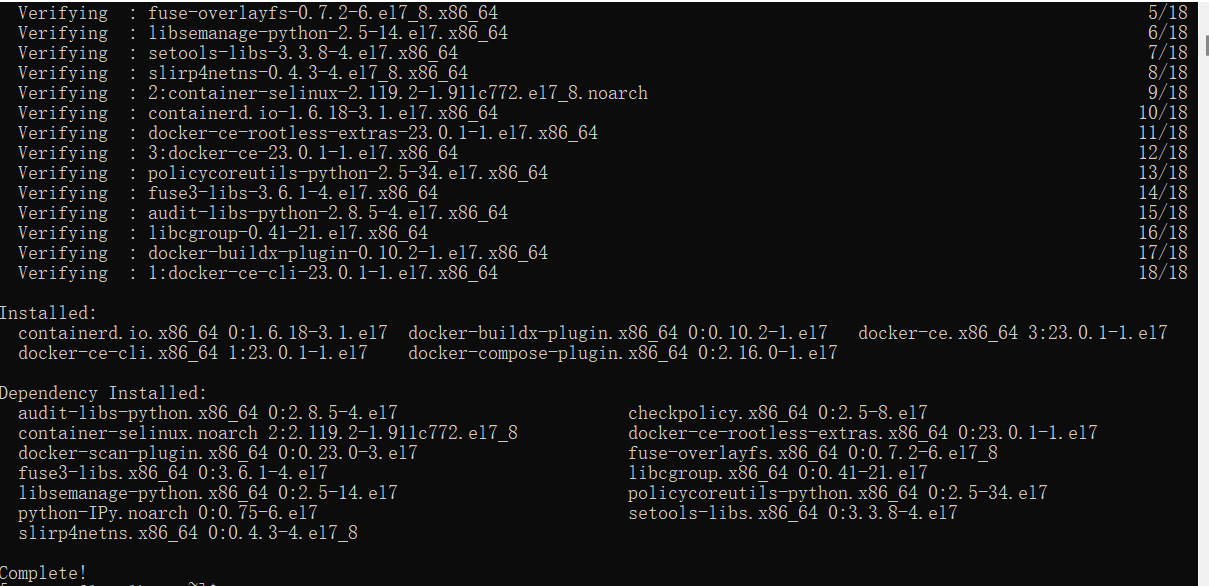
在CentOS上安装Docker引擎
1,先决条件#### 1-1操作系统要求1-2 卸载旧版本 2,安装方法2-1使用存储库安装设置存储库安装 Docker 引擎 本文永久更新地址: 官方地址:https://docs.docker.com/engine/install/centos/ 1,先决条件 #### 1-1操作系统要求 要安装 Docker Engine,您需要…...

【10】核心易中期刊推荐——模式识别与机器学习
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

【数据结构】并查集
目录 一:用途 二:实现 O(1) 三:例题 例题1:集合 例题2:连通图无向 例题3:acwing 240 食物链 一:用途 将两个集合合并询问两个元素是否在一个集合当中 二:实现 O(1) 每…...

软考--网络攻击分类
网络攻击的主要手段包括口令入侵、放置特洛伊木马程序、拒绝服务(DoS)攻击、端口扫描、网络监听、欺骗攻击和电子邮件攻击等。口令入侵是指使用某些合法用户的账号和口令登录到目的主机,然后再实施攻击活动。特洛伊木马(Trojans)程序常被伪装…...

蓝桥杯刷题冲刺 | 倒计时17天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.长草2.分考场1.长草 题目 链接: 长草 - 蓝桥云课 (lanqiao.cn) 题目描述 小明有一…...

冲击蓝桥杯-并查集,前缀和,字符串
目录 前言 一、并查集 1、并查集的合并(带路径压缩) 2、询问是否为同一个集合 3、例题 二、前缀和 1 、前缀和是什么 2、经典题目 三- 字符串处理 1、字符串的插入 2、字符串转化为int类型 3、字符反转 前言 并查集合前缀,字符串…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
