矩阵中的最大得分(Lc3148)——动态规划
给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。
你可以从 任一 单元格开始,并且必须至少移动一次。
返回你能得到的 最大 总得分。
示例 1:

输入:grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]
输出:9
解释:从单元格 (0, 1) 开始,并执行以下移动:
- 从单元格 (0, 1) 移动到 (2, 1),得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2),得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。
示例 2:
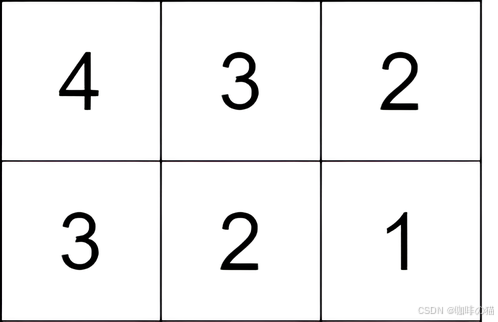
输入:grid = [[4,3,2],[3,2,1]]
输出:-1
解释:从单元格 (0, 0) 开始,执行一次移动:从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 105
问题简要描述:返回最大总得分
细节阐述:
- f[i][j] 表示以 (i,j) 为终点的路径的最小值
Java
class Solution {public int maxScore(List<List<Integer>> grid) {int m = grid.size(), n = grid.get(0).size();int[][] f = new int[m + 1][n + 1];int inf = 1 << 30, ans = -inf;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int min = inf;if (i > 0) {min = Math.min(min, f[i - 1][j]);}if (j > 0) {min = Math.min(min, f[i][j - 1]);}ans = Math.max(ans, grid.get(i).get(j) - min);f[i][j] = Math.min(grid.get(i).get(j), min);}}return ans;}
}Python3
class Solution:def maxScore(self, grid: List[List[int]]) -> int:f = [[0] * len(grid[0]) for _ in range(len(grid))]ans = -inffor i, row in enumerate(grid):for j, x in enumerate(row):mi = infif i:mi = min(mi, f[i - 1][j])if j:mi = min(mi, f[i][j - 1])ans = max(ans, grid[i][j] - mi)f[i][j] = min(grid[i][j], mi)return ansTypeScript
function maxScore(grid: number[][]): number {const [m, n] = [grid.length, grid[0].length];const f = Array.from({length: m}, () => Array.from({length: n}, () => 0));let ans = -Infinity;for (let i = 0; i < m; i++) {for (let j = 0; j < n; j++) {let min = Infinity;if (i > 0) {min = Math.min(min, f[i - 1][j]);}if (j > 0) {min = Math.min(min, f[i][j - 1]);}ans = Math.max(ans, grid[i][j] - min);f[i][j] = Math.min(grid[i][j], min);}}return ans;
};C++
class Solution {
public:int maxScore(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int f[m][n];int inf = 1 << 30, ans = -inf;for (int i = 0;i < m;i++) {for (int j = 0;j < n;j++) {int mi = inf;if (i > 0) {mi = min(mi, f[i - 1][j]);}if (j > 0) {mi = min(mi, f[i][j - 1]);}ans = max(ans, grid[i][j] - mi);f[i][j] = min(grid[i][j], mi);}}return ans; }
};Go
func maxScore(grid [][]int) int {m, n := len(grid), len(grid[0])f := make([][]int, m)for i := range f {f[i] = make([]int, n)}const inf int = 1 << 30ans := -inffor i, row := range grid {for j, x := range row {mi := infif i > 0 {mi = min(mi, f[i-1][j])}if j > 0 {mi = min(mi, f[i][j-1])}ans = max(ans, x-mi)f[i][j] = min(x, mi)}}return ans
}相关文章:

矩阵中的最大得分(Lc3148)——动态规划
给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。 你可以从 任一 单元格开始,并且必须…...
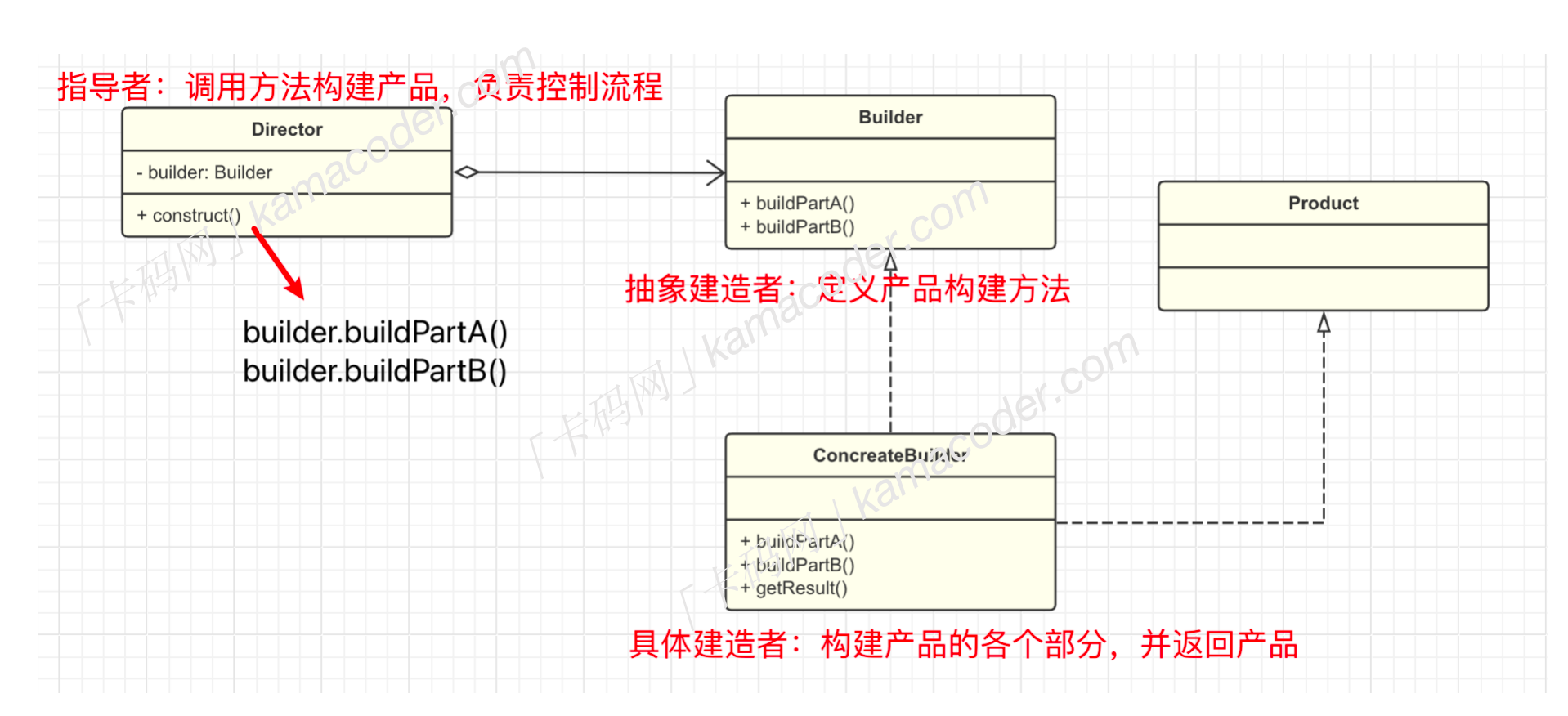
C++ 设计模式(4. 建造者模式)
建造者模式(也被成为生成器模式),是一种创建型设计模式,软件开发过程中有的时候需要创建很复杂的对象,而建造者模式的主要思想是将对象的构建过程分为多个步骤,并为每个步骤定义一个抽象的接口。具体的构建…...

Arbitrum 和 Optimism Layer 2 扩展方案对比
Arbitrum 和 Optimism 对比分析 Arbitrum 和 Optimism 是两个以太坊 Layer 2 扩展方案,它们都使用了 Optimistic Rollup 技术来提升以太坊的可扩展性并降低交易成本。虽然它们有着相似的目标,但在架构设计、性能表现和费用结构上各有特点。 一、架构与…...

热门的蓝牙耳机中,哪种类型更受欢迎?四款热度高的开放式耳机
在如今的耳机市场中,开放式耳机异军突起,成为了众多消费者的新宠。如果你还在为传统入耳式耳机带来的不适而烦恼,那么开放式耳机绝对值得你一试。它不仅能让你在享受音乐的同时,依然可以清晰感知周围环境,保障你的安全…...

基于web的亚热带常见自然林病虫害识别系统——总结与展望
文章目录 一、前言二、总结三、展望参考文献致谢一、前言 这个系列也迎来了结尾,最后说一些碎碎念… 二、总结 本文首先简要介绍了卷积神经网络的基本原理,以及在亚热带常见自然林植物识别领域的研究应用现状。 其重点研究了卷积神经网络在亚热带常见自然林植物叶片病害识…...

其他自动重试的注解
除了 Retryable 注解之外,Spring 提供了其他注解用于自动重试方法,主要包括以下几个注解: 1. Recover Recover 注解用于定义重试次数耗尽后执行的恢复方法。当 Retryable 注解的重试次数达到上限时,Recover 方法会被调用。这通常…...
宠物空气净化器哪款能吸毛?希喂、米家宠物空气净化器测评分享
养猫最令人困扰的,就是掉毛与难以彻底消除的异味,这两个问题就成了养猫生活中的一大挑战。每当换季或是猫咪自我梳理时,家中便被一层细腻的绒毛覆盖,从地板到沙发,从床单到衣物,甚至是空气中都漂浮着细小的…...
)
讲清前端开发(入门)
前端开发:创建用户在网页或应用程序中直接与之交互的部分。 简单来说,就是负责打造用户在使用网站、网页应用或者移动应用时直接看到和与之交互的部分。打个比方,前端开发就像是给房子做装修。房子的框架结构已经有了,但是需要有…...

深入理解MySQL索引:原理、数据结构与优化策略
深入理解MySQL索引:原理、数据结构与优化策略 MySQL 是当今最流行的开源关系型数据库管理系统之一,其强大的性能与灵活的可扩展性使得它广泛应用于各种规模的应用程序中。在数据库的日常操作中,索引起着至关重要的作用,能够极大地…...

mysql数据库基础使用
1、登录mysql ① 本地登录 mysql -u 用户名 -p ②远程登入 mysql -h ip主机地址 -P 端口号 -u 用户名 -p 回车输入密码即可. 2、关于用户操作 ①创建用户 % 代表所有ip都可以访问,可指定主机ip create user 用户名% identified by 密码; ②修改密码 alte…...

GATK AlleleList接口介绍
在 GATK(Genome Analysis Toolkit)中,AlleleList 接口是一个用来表示等位基因(alleles)列表的接口。Allele 是遗传学中用于表示某一特定基因座的不同形式的一个基本单位。AlleleList 接口定义了一些操作,使得处理和访问一组等位基因更加方便。 AlleleList 的实现类和继承…...

直播App遭受抓包后的DDoS与CC攻击防御策略
随着直播应用的普及,越来越多的用户开始依赖这些平台进行娱乐和社交活动。然而,这也使得直播平台成为网络攻击的目标之一。其中,DDoS(分布式拒绝服务)攻击和CC(Challenge Collapsar,即HTTP慢速攻…...

【xilinx】 AXI Quad SPI IP - 如果 s_axi_wstrb 不等于 0xf,则寄存器可能无法正确更新
PG153 (v3.2) 规定如下: “AXI4-Lite 写访问寄存器由 32 位 AXI 写数据 (* _wdata ) 信号更新,并且不受 AXI 写数据选通 (* _wstrb ) 信号的影响。” "The AXI4-Lite write access register is updated by the 32-bit AXI Write Data (* _wdata ) s…...

【EPLAN】P8 2.9 使用不了ePLUSE
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 解决 EPLAN P8 2.9 使用不了ePLUSE问题 2、 问题场景 客户反应 EPLAN P8 2.9 版本打开后使用不了 ePLUSE 功能,如图 1 所示 EPLAN ePLUSE 界面为空白状态,无法使用。 图 1 3、软硬件环境 …...

页面设计任务 个人简介页面
目录 任务要求 任务讲解 源码: 详细讲解 html部分 CSS部分 任务要求 页面结构: 创建一个基本的 HTML 页面,页面标题为“我的个人简介”。页面内容分为以下四个部分: 顶部导航栏: 包含至少三个导航链接,例如:“主页”、“关于…...

机械学习—零基础学习日志(如何理解概率论3)
随机变量的函数分布 一维随机变量分布,可以看到下图,X为不同情况的概率。而x如果是大于等于X,那么当x在40以内时,没有概率,为0。 当x变大,在40-80之间,那么x大于X的概率为,0.7&…...

YOLOv8添加SE注意力机制有效提升检测精度(已跑通)
SE注意力机制概念 SSqueeze-and-Excitation (SE) 注意力机制是一种专注于增强网络模型对不同特征通道的重要性理解的机制。它通过对通道维度上的特征进行动态调整,增强了网络对重要特征的敏感性。 源码 import numpy as np import torch from torch import nn fro…...

【正点原子K210连载】第三十二章 音频FFT实验 摘自【正点原子】DNK210使用指南-CanMV版指南
第三十二章 音频FFT实验 本章将介绍CanMV下FFT的应用,通过将时域采集到的音频数据通过FFT为频域。通过本章的学习,读者将学习到CanMV下控制FFT加速器进行FFT的使用。 本章分为如下几个小节: 32.1 maix.FFT模块介绍 32.2 硬件设计 32.3 程序设…...
Android Studio修改默认.m2与Gradle user home缓存位置
Android Studio修改默认.m2与Gradle user home缓存位置 1、修改Gradle user home的方法: android studio配置默认.gradle路径_android studio gradle在哪-CSDN博客文章浏览阅读2k次。当android studio新建一个项目时候,默认的.gradle路径均认为是在c盘的…...

BFS解决单源最短路问题
目录 迷宫中离入口最近的出口 最小基因变化 单词接龙 为高尔夫比赛砍树 迷宫中离入口最近的出口 题目 思路 使用宽度优先遍历解决这道题,需要一个二维数组标记是否被遍历过,也需要一个队列辅助完成宽度优先遍历,类似于水波纹一样&#x…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
