【题解】—— LeetCode一周小结32
🌟欢迎来到 我的博客 —— 探索技术的无限可能!
🌟博客的简介(文章目录)
【题解】—— 每日一道题目栏
上接:【题解】—— LeetCode一周小结31
5.不含连续1的非负整数
题目链接:600. 不含连续1的非负整数
给定一个正整数 n ,请你统计在 [0, n] 范围的非负整数中,有多少个整数的二进制表示中不存在 连续的 1 。
示例 1:
输入: n = 5
输出: 5
解释:
下面列出范围在 [0, 5] 的非负整数与其对应的二进制表示:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
其中,只有整数 3 违反规则(有两个连续的 1 ),其他 5 个满足规则。
示例 2:
输入: n = 1
输出: 2
示例 3:
输入: n = 2
输出: 3
提示:
1 <= n <= 109
题解:
方法:数位 DP
class Solution {public int findIntegers(int n) {int m = Integer.SIZE - Integer.numberOfLeadingZeros(n);int[][] memo = new int[m][2];for (int[] row : memo) {Arrays.fill(row, -1); // -1 表示没有计算过}return dfs(m - 1, 0, true, n, memo); // 从高位到低位}// pre 表示前一个比特位填的数private int dfs(int i, int pre, boolean isLimit, int n, int[][] memo) {if (i < 0) {return 1;}if (!isLimit && memo[i][pre] >= 0) { // 之前计算过return memo[i][pre];}int up = isLimit ? n >> i & 1 : 1;int res = dfs(i - 1, 0, isLimit && up == 0, n, memo); // 填 0if (pre == 0 && up == 1) { // 可以填 1res += dfs(i - 1, 1, isLimit, n, memo); // 填 1}if (!isLimit) {memo[i][pre] = res; // 记忆化}return res;}
}
6.找出所有稳定的二进制数组 I
题目链接:3129. 找出所有稳定的二进制数组 I
给你 3 个正整数 zero ,one 和 limit 。
一个
二进制数组
arr 如果满足以下条件,那么我们称它是 稳定的 :
0 在 arr 中出现次数 恰好 为 zero 。
1 在 arr 中出现次数 恰好 为 one 。
arr 中每个长度超过 limit 的
子数组
都 同时 包含 0 和 1 。
请你返回 稳定 二进制数组的 总 数目。
由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:zero = 1, one = 1, limit = 2
输出:2
解释:
两个稳定的二进制数组为 [1,0] 和 [0,1] ,两个数组都有一个 0 和一个 1 ,且没有子数组长度大于 2 。
示例 2:
输入:zero = 1, one = 2, limit = 1
输出:1
解释:
唯一稳定的二进制数组是 [1,0,1] 。
二进制数组 [1,1,0] 和 [0,1,1] 都有长度为 2 且元素全都相同的子数组,所以它们不稳定。
示例 3:
输入:zero = 3, one = 3, limit = 2
输出:14
解释:
所有稳定的二进制数组包括 [0,0,1,0,1,1] ,[0,0,1,1,0,1] ,[0,1,0,0,1,1]
,[0,1,0,1,0,1] ,[0,1,0,1,1,0] ,[0,1,1,0,0,1] ,[0,1,1,0,1,0]
,[1,0,0,1,0,1] ,[1,0,0,1,1,0] ,[1,0,1,0,0,1] ,[1,0,1,0,1,0]
,[1,0,1,1,0,0] ,[1,1,0,0,1,0] 和 [1,1,0,1,0,0] 。
提示:
1 <= zero, one, limit <= 200
题解:
方法:动态规划
class Solution {public int numberOfStableArrays(int zero, int one, int limit) {final int mod = (int) 1e9 + 7;long[][][] f = new long[zero + 1][one + 1][2];for (int i = 1; i <= Math.min(zero, limit); ++i) {f[i][0][0] = 1;}for (int j = 1; j <= Math.min(one, limit); ++j) {f[0][j][1] = 1;}for (int i = 1; i <= zero; ++i) {for (int j = 1; j <= one; ++j) {long x = i - limit - 1 < 0 ? 0 : f[i - limit - 1][j][1];long y = j - limit - 1 < 0 ? 0 : f[i][j - limit - 1][0];f[i][j][0] = (f[i - 1][j][0] + f[i - 1][j][1] - x + mod) % mod;f[i][j][1] = (f[i][j - 1][0] + f[i][j - 1][1] - y + mod) % mod;}}return (int) ((f[zero][one][0] + f[zero][one][1]) % mod);}
}
7.找出所有稳定的二进制数组 II
题目链接:3130. 找出所有稳定的二进制数组 II
给你 3 个正整数 zero ,one 和 limit 。
一个
二进制数组
arr 如果满足以下条件,那么我们称它是 稳定的 :
0 在 arr 中出现次数 恰好 为 zero 。
1 在 arr 中出现次数 恰好 为 one 。
arr 中每个长度超过 limit 的
子数组
都 同时 包含 0 和 1 。
请你返回 稳定 二进制数组的 总 数目。
由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:zero = 1, one = 1, limit = 2
输出:2
解释:
两个稳定的二进制数组为 [1,0] 和 [0,1] ,两个数组都有一个 0 和一个 1 ,且没有子数组长度大于 2 。
示例 2:
输入:zero = 1, one = 2, limit = 1
输出:1
解释:
唯一稳定的二进制数组是 [1,0,1] 。
二进制数组 [1,1,0] 和 [0,1,1] 都有长度为 2 且元素全都相同的子数组,所以它们不稳定。
示例 3:
输入:zero = 3, one = 3, limit = 2
输出:14
解释:
所有稳定的二进制数组包括 [0,0,1,0,1,1] ,[0,0,1,1,0,1] ,[0,1,0,0,1,1]
,[0,1,0,1,0,1] ,[0,1,0,1,1,0] ,[0,1,1,0,0,1] ,[0,1,1,0,1,0]
,[1,0,0,1,0,1] ,[1,0,0,1,1,0] ,[1,0,1,0,0,1] ,[1,0,1,0,1,0]
,[1,0,1,1,0,0] ,[1,1,0,0,1,0] 和 [1,1,0,1,0,0] 。
提示:
1 <= zero, one, limit <= 1000
题解:
方法:递推
class Solution {public int numberOfStableArrays(int zero, int one, int limit) {final int MOD = 1_000_000_007;int[][][] f = new int[zero + 1][one + 1][2];for (int i = 1; i <= Math.min(limit, zero); i++) {f[i][0][0] = 1;}for (int j = 1; j <= Math.min(limit, one); j++) {f[0][j][1] = 1;}for (int i = 1; i <= zero; i++) {for (int j = 1; j <= one; j++) {// + MOD 保证答案非负f[i][j][0] = (int) (((long) f[i - 1][j][0] + f[i - 1][j][1] + (i > limit ? MOD - f[i - limit - 1][j][1] : 0)) % MOD);f[i][j][1] = (int) (((long) f[i][j - 1][0] + f[i][j - 1][1] + (j > limit ? MOD - f[i][j - limit - 1][0] : 0)) % MOD);}}return (f[zero][one][0] + f[zero][one][1]) % MOD;}
}
8.找出与数组相加的整数 I
题目链接:3131. 找出与数组相加的整数 I
给你两个长度相等的数组 nums1 和 nums2。
数组 nums1 中的每个元素都与变量 x 所表示的整数相加。如果 x 为负数,则表现为元素值的减少。
在与 x 相加后,nums1 和 nums2 相等 。当两个数组中包含相同的整数,并且这些整数出现的频次相同时,两个数组 相等 。
返回整数 x 。
示例 1:
输入:nums1 = [2,6,4], nums2 = [9,7,5]
输出:3
解释:
与 3 相加后,nums1 和 nums2 相等。
示例 2:
输入:nums1 = [10], nums2 = [5]
输出:-5
解释:
与 -5 相加后,nums1 和 nums2 相等。
示例 3:
输入:nums1 = [1,1,1,1], nums2 = [1,1,1,1]
输出:0
解释:
与 0 相加后,nums1 和 nums2 相等。
提示:
1 <= nums1.length == nums2.length <= 100
0 <= nums1[i], nums2[i] <= 1000
测试用例以这样的方式生成:存在一个整数 x,使得 nums1 中的每个元素都与 x 相加后,nums1 与 nums2 相等。
题解:
方法:数学
class Solution {public int addedInteger(int[] nums1, int[] nums2) {return min(nums2) - min(nums1);}private int min(int[] nums) {int res = Integer.MAX_VALUE;for (int x : nums) {res = Math.min(res, x);}return res;}
}
9.找出与数组相加的整数 II
题目链接:3132. 找出与数组相加的整数 II
给你两个整数数组 nums1 和 nums2。
从 nums1 中移除两个元素,并且所有其他元素都与变量 x 所表示的整数相加。如果 x 为负数,则表现为元素值的减少。
执行上述操作后,nums1 和 nums2 相等 。当两个数组中包含相同的整数,并且这些整数出现的频次相同时,两个数组 相等 。
返回能够实现数组相等的 最小 整数 x 。
示例 1:
输入:nums1 = [4,20,16,12,8], nums2 = [14,18,10]
输出:-2
解释:
移除 nums1 中下标为 [0,4] 的两个元素,并且每个元素与 -2 相加后,nums1 变为 [18,14,10] ,与 nums2
相等。
示例 2:
输入:nums1 = [3,5,5,3], nums2 = [7,7]
输出:2
解释:
移除 nums1 中下标为 [0,3] 的两个元素,并且每个元素与 2 相加后,nums1 变为 [7,7] ,与 nums2 相等。
提示:
3 <= nums1.length <= 200
nums2.length == nums1.length - 2
0 <= nums1[i], nums2[i] <= 1000
测试用例以这样的方式生成:存在一个整数 x,nums1 中的每个元素都与 x 相加后,再移除两个元素,nums1 可以与 nums2 相等。
题解:
方法:O(nlogn) 排序+判断子序列
class Solution {public int minimumAddedInteger(int[] nums1, int[] nums2) {Arrays.sort(nums1);Arrays.sort(nums2);// 枚举保留 nums1[2] 或者 nums1[1] 或者 nums1[0]// 倒着枚举是因为 nums1[i] 越大答案越小,第一个满足的就是答案for (int i = 2; i > 0; i--) {int x = nums2[0] - nums1[i];// 在 {nums1[i] + x} 中找子序列 nums2int j = 0;for (int k = i; k < nums1.length; k++) {if (nums2[j] == nums1[k] + x && ++j == nums2.length) {// nums2 是 {nums1[i] + x} 的子序列return x;}}}// 题目保证答案一定存在return nums2[0] - nums1[0];}
}10.找到 Alice 和 Bob 可以相遇的建筑
题目链接:2940. 找到 Alice 和 Bob 可以相遇的建筑
给你一个下标从 0 开始的正整数数组 heights ,其中 heights[i] 表示第 i 栋建筑的高度。
如果一个人在建筑 i ,且存在 i < j 的建筑 j 满足 heights[i] < heights[j] ,那么这个人可以移动到建筑 j 。
给你另外一个数组 queries ,其中 queries[i] = [ai, bi] 。第 i 个查询中,Alice 在建筑 ai ,Bob 在建筑 bi 。
请你能返回一个数组 ans ,其中 ans[i] 是第 i 个查询中,Alice 和 Bob 可以相遇的 最左边的建筑 。如果对于查询 i ,Alice 和 Bob 不能相遇,令 ans[i] 为 -1 。
示例 1:
输入:heights = [6,4,8,5,2,7], queries = [[0,1],[0,3],[2,4],[3,4],[2,2]]
输出:[2,5,-1,5,2]
解释:第一个查询中,Alice 和 Bob 可以移动到建筑 2 ,因为 heights[0] < heights[2] 且
heights[1] < heights[2] 。第二个查询中,Alice 和 Bob 可以移动到建筑 5 ,因为 heights[0] < heights[5] 且 heights[3]
< heights[5] 。第三个查询中,Alice 无法与 Bob 相遇,因为 Alice 不能移动到任何其他建筑。
第四个查询中,Alice 和 Bob 可以移动到建筑 5 ,因为 heights[3] < heights[5] 且 heights[4]
< heights[5] 。第五个查询中,Alice 和 Bob 已经在同一栋建筑中。
对于 ans[i] != -1 ,ans[i] 是 Alice 和 Bob 可以相遇的建筑中最左边建筑的下标。
对于 ans[i] == -1 ,不存在 Alice 和 Bob 可以相遇的建筑。
示例 2:
输入:heights = [5,3,8,2,6,1,4,6], queries =
[[0,7],[3,5],[5,2],[3,0],[1,6]]输出:[7,6,-1,4,6]
解释:第一个查询中,Alice 可以直接移动到 Bob 的建筑,因为 heights[0] < heights[7] 。
第二个查询中,Alice 和 Bob 可以移动到建筑 6 ,因为 heights[3] < heights[6] 且 heights[5]
< heights[6] 。第三个查询中,Alice 无法与 Bob 相遇,因为 Bob 不能移动到任何其他建筑。
第四个查询中,Alice 和 Bob 可以移动到建筑 4 ,因为 heights[3] < heights[4] 且 heights[0]
< heights[4] 。第五个查询中,Alice 可以直接移动到 Bob 的建筑,因为 heights[1] < heights[6] 。
对于 ans[i] != -1 ,ans[i] 是 Alice 和 Bob 可以相遇的建筑中最左边建筑的下标。
对于 ans[i] == -1 ,不存在 Alice 和 Bob 可以相遇的建筑。
提示:
1 <= heights.length <= 5 * 104
1 <= heights[i] <= 109
1 <= queries.length <= 5 * 104
queries[i] = [ai, bi]
0 <= ai, bi <= heights.length - 1
题解:
方法1:离线+最小堆
class Solution {public int[] leftmostBuildingQueries(int[] heights, int[][] queries) {int[] ans = new int[queries.length];Arrays.fill(ans, -1);List<int[]>[] qs = new ArrayList[heights.length];Arrays.setAll(qs, i -> new ArrayList<>());for (int i = 0; i < queries.length; i++) {int a = queries[i][0];int b = queries[i][1];if (a > b) {int tmp = a;a = b;b = tmp; // 保证 a <= b}if (a == b || heights[a] < heights[b]) {ans[i] = b; // a 直接跳到 b} else {qs[b].add(new int[]{heights[a], i}); // 离线询问}}PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);for (int i = 0; i < heights.length; i++) {while (!pq.isEmpty() && pq.peek()[0] < heights[i]) {// 堆顶的 heights[a] 可以跳到 heights[i]ans[pq.poll()[1]] = i;}for (int[] q : qs[i]) {pq.offer(q); // 后面再回答}}return ans;}
}
方法2:离线+单调栈二分
class Solution {public int[] leftmostBuildingQueries(int[] heights, int[][] queries) {int n = heights.length;int[] ans = new int[queries.length];List<int[]>[] qs = new ArrayList[n];Arrays.setAll(qs, i -> new ArrayList<>());for (int i = 0; i < queries.length; i++) {int a = queries[i][0];int b = queries[i][1];if (a > b) {int tmp = a;a = b;b = tmp; // 保证 a <= b}if (a == b || heights[a] < heights[b]) {ans[i] = b; // a 直接跳到 b} else {qs[b].add(new int[]{heights[a], i}); // 离线询问}}int[] st = new int[n];int top = 0;for (int i = n - 1; i >= 0; i--) {for (int[] q : qs[i]) {ans[q[1]] = binarySearch(heights, st, top, q[0]);}while (top > 0 && heights[i] >= heights[st[top - 1]]) {top--;}st[top++] = i;}return ans;}// 返回 st 中最后一个 > x 的高度的下标// 如果不存在,返回 -1// https://www.bilibili.com/video/BV1AP41137w7/private int binarySearch(int[] heights, int[] st, int right, int x) {int left = -1; // 开区间 (left, right)while (left + 1 < right) { // 开区间不为空int mid = (left + right) >>> 1;if (heights[st[mid]] > x) {left = mid; // 范围缩小到 (mid, right)} else {right = mid; // 范围缩小到 (left, mid)}}return left < 0 ? -1 : st[left];}
}
方法3:在线+线段树二分
class Solution {public int[] leftmostBuildingQueries(int[] heights, int[][] queries) {int n = heights.length;mx = new int[2 << (Integer.SIZE - Integer.numberOfLeadingZeros(n))];build(1, 0, n - 1, heights);int[] ans = new int[queries.length];for (int i = 0; i < queries.length; i++) {int a = queries[i][0];int b = queries[i][1];if (a > b) {int tmp = a;a = b;b = tmp; // 保证 a <= b}if (a == b || heights[a] < heights[b]) {ans[i] = b; // a 直接跳到 b} else {// 线段树二分,找 [b+1,n-1] 中的第一个 > heights[a] 的位置ans[i] = query(1, 0, n - 1, b + 1, heights[a]);}}return ans;}private int[] mx;// 用 heights 初始化线段树,维护区间最大值private void build(int o, int l, int r, int[] heights) {if (l == r) {mx[o] = heights[l];return;}int m = (l + r) / 2;build(o * 2, l, m, heights);build(o * 2 + 1, m + 1, r, heights);mx[o] = Math.max(mx[o * 2], mx[o * 2 + 1]);}// 返回 [L,n-1] 中第一个 > v 的值的下标// 如果不存在,返回 -1private int query(int o, int l, int r, int L, int v) {if (mx[o] <= v) { // 区间最大值 <= vreturn -1; // 没有 > v 的数}if (l == r) { // 找到了return l;}int m = (l + r) / 2;if (L <= m) {int pos = query(o * 2, l, m, L, v); // 递归左子树if (pos >= 0) { // 找到了return pos;}}return query(o * 2 + 1, m + 1, r, L, v); // 递归右子树}
}
11.不相交的线
题目链接:1035. 不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
输入:nums1 = [1,4,2], nums2 = [1,2,4]
输出:2
解释:可以画出两条不交叉的线,如上图所示。
但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到
nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出:2
提示:
1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000
题解:
方法:动态规划
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int m = nums1.length, n = nums2.length;int[][] f = new int[m + 1][n + 1];for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (nums1[i - 1] == nums2[j - 1]) {f[i][j] = f[i - 1][j - 1] + 1;} else {f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);}}}return f[m][n];}
}
下接:【题解】—— LeetCode一周小结33
相关文章:

【题解】—— LeetCode一周小结32
🌟欢迎来到 我的博客 —— 探索技术的无限可能! 🌟博客的简介(文章目录) 【题解】—— 每日一道题目栏 上接:【题解】—— LeetCode一周小结31 5.不含连续1的非负整数 题目链接:600. 不含连续…...
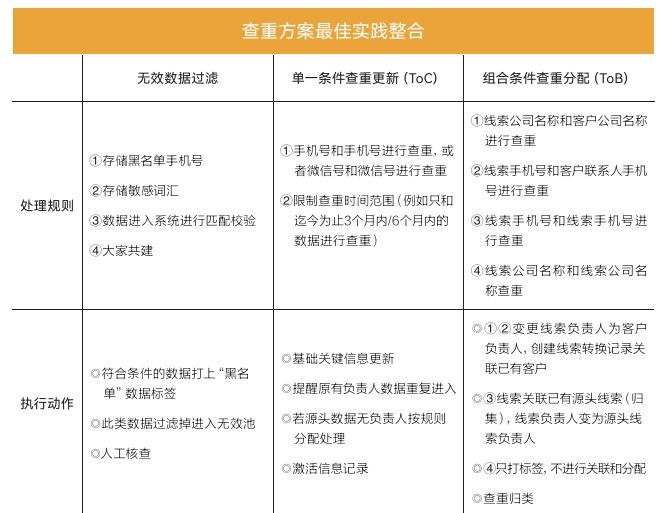
详解线索分层的目的、维度与创新实践
线索分层是一个系统性的过程,旨在更有效地管理、跟踪和利用线索资源。这一过程可以借鉴多种策略和方法,特别是在用户运营和市场营销中。 1、线索分层的目的 线索分层的主要目的是根据线索的不同特征或成熟度,将其分类管理,以便更…...

于8月21号的回顾
傍晚的日落和逐渐深邃的夜,驱散了白天的极致闷热。倦怠和疲惫充斥着大脑,喧嚣的浮沉又在耳边轰鸣。 我不曾想到,再次打开博客已经是两年后的今天了。手指轻轻滑过鼠标,博客的页面缓缓加载,那些被时间尘封的记忆瞬间涌…...

Abstract Class抽象类
抽象类(Abstract Class)在面向对象编程中是一种特殊的类,它不能被实例化,即不能创建该类的对象。抽象类主要用于定义一组接口(即方法),这些方法的具体实现由子类来完成。抽象类通常用于表示一种…...

webrtc ns 降噪之粉红噪声参数推导
webrtc中降噪中,前50帧需要进行简单噪声估计,使用白噪声和粉红噪声模型估算。 首先我们 复习 有色噪声(包含白噪声)的一般模型: S(f) 是频率 f 处的功率谱密度。f是频率。α 是一个频谱指数,通常在1左右。…...

IO进程线程8月21日
1,思维导图 2,登录 #ifndef __LOG_H__ #define __LOG_H__ #include<myhead.h> typedef struct {char name[20];char pwd[20]; }str;int regist();int login(); #endif#include"log.h" int login() {char a[20]"\n";str p,s;…...

Web安全:SqlMap工具
一、简介 sqlmap 是一款开源的渗透测试工具,可以自动化进行SQL注入的检测、利用,并能接管数据库服务器。它具有功能强大的检测引擎,为渗透测试人员提供了许多专业的功能并且可以进行组合,其中包括数据库指纹识别、数据读取和访问底层文件系统…...
用手机写一本电子书
第1步、进入Andi.cn网站 第2步、点击登录,注册用户 第3步、点击去创作,进入创作页面 第4步、点击右下角的小笔,写一篇文章 第5步、下翻,点击提交按钮 第6步、再写一篇文章 第7步、点击栏目设计 第8步、进入栏目设计,点…...

【网络编程】基于UDP的TFTP文件传输
1)tftp协议概述 简单文件传输协议,适用于在网络上进行文件传输的一套标准协议,使用UDP传输 特点: 是应用层协议 基于UDP协议实现 数据传输模式 octet:二进制模式(常用) mail:已经不再…...

Vue 3 + Pinia 实现网页刷新功能
概述 在现代 Web 开发中,保持用户界面的动态性和响应性至关重要。当用户触发某些操作时,例如点击按钮或者完成表单提交,我们往往需要刷新页面的一部分来展示最新的数据。本文将介绍如何使用 Vue 3 和 Pinia 来实现这一功能。 技术栈 Vue 3…...
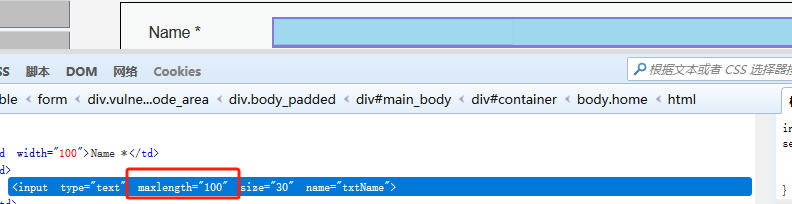
DVWA综合靶场漏洞讲解
目录 综合靶场漏洞讲解 Brute Force Low Medium High Command Injection Low Medium High File Inclusion Low,Medium,High File Upload Low Medium High SQL Injection Low Medium High SQL Injection (Blind) Low Medium High XSS(DOM&am…...

实现Bezier样条曲线
1.给出n1 个控制点pk(xk,yk,zk),这里k可取值0-n,多项式函数公式如下 获取的单个点的代码 void zmBezier::getPoint(float u, double p[3]) {int n m_count - 1;double x 0, y 0, z 0;for(int k 0; k < n; k){x m_ctrlPoints[k][0] * BEZ_k_n(n, k, u);y m_ctrlPoin…...

MySQL中的EXPLAIN的详解
一、介绍 官网介绍: https://dev.mysql.com/doc/refman/5.7/en/explain-output.htmlhttps://dev.mysql.com/doc/refman/8.0/en/explain-output.htmlexplain(执行计划),使用explain关键字可以模拟优化器执行sql查询语句ÿ…...

LearnOpenGL——SSAO学习笔记
LearnOpenGL——SSAO学习笔记 SSAO一、基本概念二、样本缓冲三、法向半球四、随机核心转动五、SSAO着色器六、环境遮蔽模糊七、应用SSAO遮蔽因子 SSAO 一、基本概念 环境光照是我们加入场景总体光照中的一个固定光照常量,它被用来模拟光的散射(Scattering)。散射应…...

[C语言]-基础知识点梳理-文件管理
前言 各位师傅们好,我是qmx_07,今天给大家讲解文件管理的相关知识,也就是常见的 读取,删除一类的操作 文件 为什么要使用文件? 程序的数据是存储在电脑的内存中,如果程序退出,内存回收&…...
pcdn闲置带宽被动收入必看教程。第五讲:光猫更换和基础设置
PCDN闲置带宽被动收入必看教程 —— 第五讲:光猫更换和基础设置 为了从闲置带宽中获得被动收入,高效的网络设备至关重要。运营商提供的光猫通常能满足日常家用需求,但对于PCDN应用来说,它们可能不足以提供所需的高性能和稳定性。…...

工业数据采集网关简介-天拓四方
随着工业4.0和物联网(IoT)技术的深入发展,工业数据采集网关作为连接现场设备与上层管理系统的关键节点,其在智能工厂中的作用愈发凸显。本文将深入探讨工业数据采集网关的功能、特点、应用场景及其实操性,以期为读者提…...

Java 调整字符串,验证码生成
package text7;public class ZiFanz {public static void main(String[] args) {//1.定义两个字符串String strA "abcde";String strB "deabc";//2.abcde->bcdea->cdeab->deabc旋转字符串//旋转并比较boolean result cheak(strA, strB);System…...

【专题】全球商用服务机器人市场研究(2023)报告合集PDF分享(附原数据表)
原文链接:https://tecdat.cn/?p37366 近年来,随着人工智能、物联网和自动化技术的不断进步,商用服务机器人行业迅速崛起,展现出广阔的发展前景。从最初的实验室研发到如今的规模化应用,商用服务机器人已逐渐成为各行…...

SQL UA注入 (injection 第十八关)
简介 SQL注入(SQL Injection)是一种常见的网络攻击方式,通过向SQL查询中插入恶意的SQL代码,攻击者可以操控数据库,SQL注入是一种代码注入攻击,其中攻击者将恶意的SQL代码插入到应用程序的输入字段中&a…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
