异或相关算法

文章目录
- 1. 异或的性质
- 2. 题目一
- 3. 题目二
- 4. 题目三
- 5. 题目四
1. 异或的性质
我们知道,异或的定义是:相同为0,相异为1。所以也被称为无进位相加,根据这定义,我们可以得出三个性质:
1. N ^ N=0。2. N ^ 0=N。3. 异或满足结合律与交换率,所以一组数据,一起异或,结果一定是同一个值。
2. 题目一
如何不创建临时变量,交换两个值?
答案是:a=a ^ b,b=a ^ b,a=a ^ b。
证明:a=a ^ b,a变了,b没变。b=a ^ b,就等于b=a ^ b ^ b,b=a ^ 0,b=a。最后一步,a=a ^ b ^ a,就是a=b ^ 0,a=b。
两个数就进行交换了,但是这个方法只能用在a与b指向不同的内存空间,如果指向同一个内存空间,这样写会把此内存置成0。
3. 题目二
怎么把一个int类型的数,提取出最右侧的1来?
什么意思呢?

就是一个数a,如何得到ans这样的值,就是把最右侧的1提取出来。
答案是:a&(-a)或者a&((~a)+1)。这个大家可以自己证明一下。
4. 题目三
一个数组中有两种数出现了奇数次,其它数都出现了偶数次,怎么找到这两个数?
解题思路:假设出现两个奇数次的是a和b。
第一步:将数组里的数全部异或,那么结果就是a ^ b,因为其它都是偶数次,异或为0。
第二步:找出a ^ b最右侧的1位置,因为a和b是不同的,所以a ^ b一定不为0,所以a ^ b二进位中一定存在1的。
第三步:a ^ b二进位中的1位置,说明a和b在此位置上是不相等的。我们就把数组中所有此位置为1的分成一组,此位置为0的分成一组。
第四步:将此位置为1的异或在一起就能得出其中一个奇数次,在异或a ^ b,就能得出另外一个奇数次。
代码实现:

5. 题目四
一个数组中有一种数出现K次,其它数都出现了M次,M>1,K<M。找到出现K次的数。要求:时间复杂度O(N),空间复杂度O(1)。
解题思路:
第一步:因为一个int类型是32位,所以我们可以先定义一个32的数组。因为是常量数组所以空间复杂度是O(1)。。
第二步:遍历数组里所有数,如果这个数的某个位置是1,我们就在32位数组中这个位置上+1。

如果是4就在下标2的位置上+1,如果是12就在下标为2和3的位置上+1。
第三步:遍历这个32位数组,如果某位置上能被M整除,说明出现K次的那个数在此位置上为0,如果此位置不能被M整除,说明此位置上出现K次的那个数此位置为1。因为K<M,所有不存在能被M整除还存在出现K次的那个数。
假设K=3,M=7,某位置上1的个数是38,38不能被7整除,说明此位置上出现K此的那个数一定为1。
第四步:定义一个变量为0,如果此位置上不能整除,我们就左移1,然后或上去。
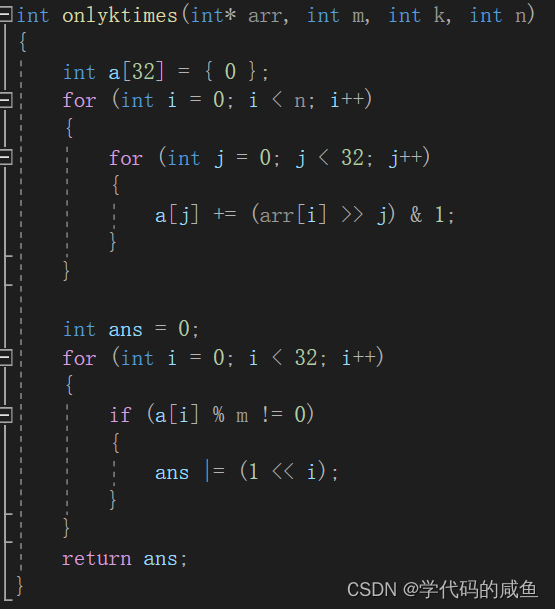
代码实现:
相关文章:

异或相关算法
文章目录1. 异或的性质2. 题目一3. 题目二4. 题目三5. 题目四1. 异或的性质 我们知道,异或的定义是:相同为0,相异为1。所以也被称为无进位相加,根据这定义,我们可以得出三个性质: 1. N ^ N0。2. N ^ 0N。3…...

python 使用pyshp读写shp文件
安装 pip install pyshp 引入 import shapefile读取 sfshapefile.Reader("{路径名}",encodingutf-8) # 仅仅读取 shapes与shape shapessf.shapes() 返回值是一个列表,包含该文件中所有的”几何数据”对象shapesf.shape(0) Shape是第1个”几何数据”…...

eNSP FTP基础配置实验
关于本实验在本实验中,我们通过两台路由器来展示通过FTP在两台路由器之间传输文件。其中一台路由器AR2作为FTP服务器,另一台路由器AR1以FTP的方式登录AR2,并对AR2的文件系统进行一些更改。实验目的熟悉华为网络设备文件系统的管理。掌握华为网…...

堆及其多种接口与堆排序的实现
我们本期来讲解堆结构 目录 堆的结构 堆的初始化 堆的销毁 堆的插入 向上调整算法 堆的删除 向下调整算法 取堆顶元素 判断堆是否为空 堆中元素个数 堆排序 向下调整与向上调整效率计算 Top-K问题 全部代码 堆的结构 堆是一种用数组模拟二叉树的结构 逻辑结构是…...
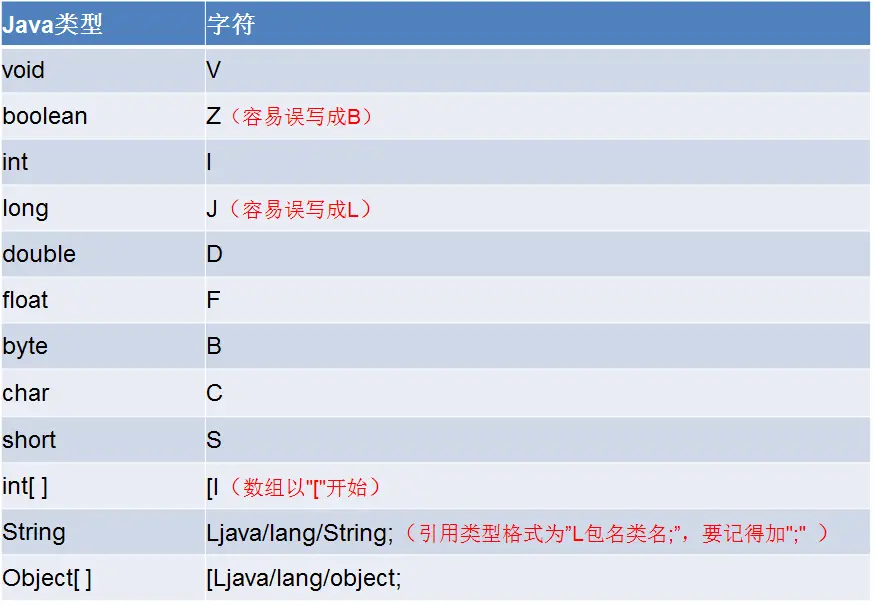
JNI原理及常用方法概述
1.1 JNI(Java Native Interface) 提供一种Java字节码调用C/C的解决方案,JNI描述的是一种技术。 1.2 NDK(Native Development Kit) Android NDK 是一组允许您将 C 或 C(“原生代码”)嵌入到 Android 应用中的工具,NDK描述的是工具集…...

【Docker】之docker-compose的介绍与命令的使用
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录docker-compose简介docker-compose基础…...
水果新鲜程度检测系统(UI界面+YOLOv5+训练数据集)
摘要:水果新鲜程度检测软件用于检测水果新鲜程度,利用深度学习技术识别腐败或损坏的水果,以辅助挑拣出新鲜水果,支持实时在线检测。本文详细介绍水果新鲜程度检测系统,在介绍算法原理的同时,给出Python的实…...

flask多并发
多线程 flask默认使用多进程处理请求,因此,是支持并发的。比如两个调用a.html和b.html, 请求a.html未运行完成,在浏览访问b.html不会阻塞。开两个不同浏览器,分别请求请求运行时间较长的a.html也不阻塞。只要不用一个…...

我用Python django开发了一个商城系统,已开源,求关注!
起始 2022年我用django开发了一个商城的第三方包,起名为:django-happy-shop。当时纯粹是利用业余时间来开发和维护这个包,想法也比较简单,Python语言做web可能用的人比较少,不一定有多少人去关注,就当是一个…...
大数据项目之数仓相关知识
第1章 数据仓库概念 数据仓库(DW): 为企业指定决策,提供数据支持的,帮助企业,改进业务流程,提高产品质量等。 DW的输入数据通常包括:业务数据,用户行为数据和爬虫数据等 ODS: 数据…...

RK3588平台开发系列讲解(视频篇)RTP H264 码流打包详解
平台内核版本安卓版本RK3588Linux 5.10Android 12文章目录 一、单 NALU 封包方式二、组合封包方式三、分片封包方式沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 H264 码流是放在 RTP 的有效载荷部分的。因此有效载荷前面的 RTP 头部跟码流本身是没有关系的,所以我…...

realloc的补充 柔性数组
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C 🔥座右铭:“不要等到什么都没有了,才下…...
【C语言】柔性数组
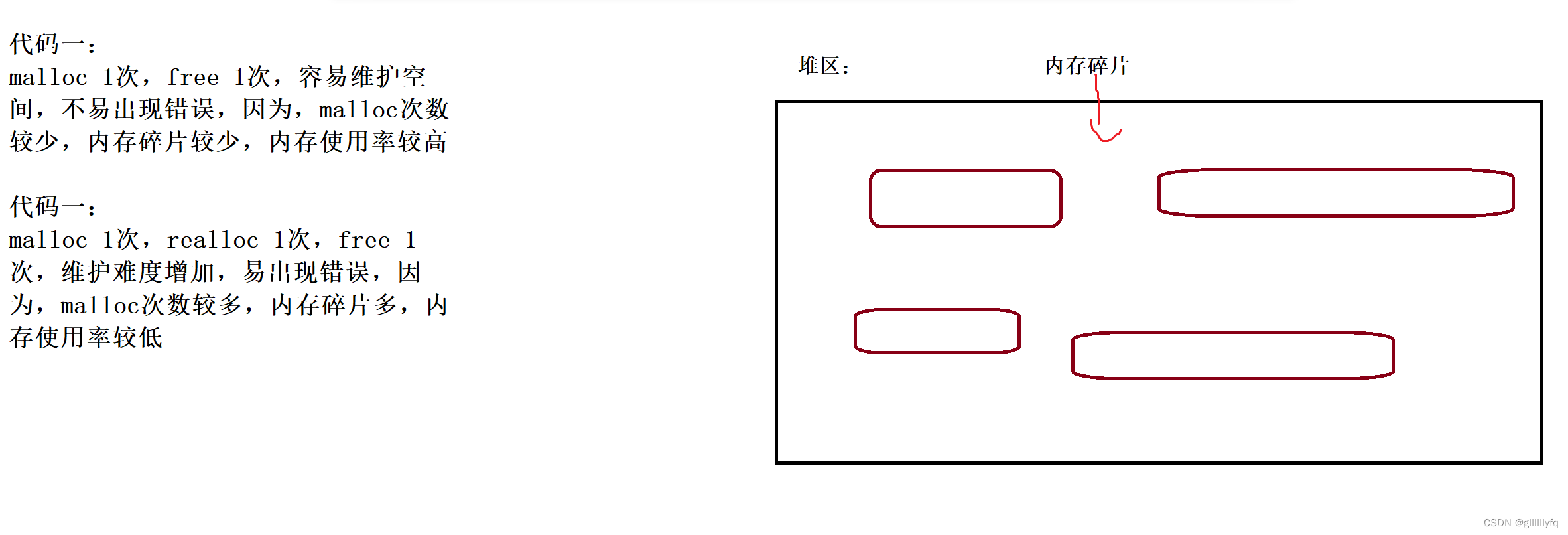
柔性数组1. 柔性数组介绍2. 柔性数组特点3. 用例3.1 代码一:3.2 代码二:4. 柔性数组优势:1. 柔性数组介绍 也许你从来没有听说过柔性数组(flexible array)这个概念,但是它确实是存在的。 C99 中,…...
【Linux】权限详解
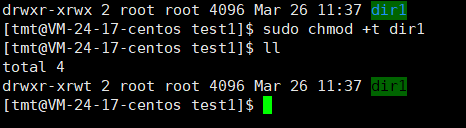
前言首先我们先来看一下权限的概念:在多用户计算机系统的管理中,权限(privilege)是指某个特定的用户具有特定的系统资源使用权力,像是文件夹,特定系统指令的使用或存储量的限制。通常,系统管理员…...

Android 之 打开相机 打开相册
Android 之 打开系统摄像头拍照 打开系统相册,并展示1,清单文件 AndroidManifest.xml<uses-permission android:name"android.permission.INTERNET" /><!--文件读取权限--><uses-permission android:name"android.permiss…...

C语言数据结构初阶(8)----栈与队列OJ题
CSDN的uu们,大家好。这里是C语言数据结构的第八讲。 目标:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:数据结构与算法栈与队列的知识点我➡➡队列相关点我➡➡栈相关2. 用栈实现队列原题链接…...

JavaScript——原型对象
JavaScript——原型对象专题 文章目录JavaScript——原型对象专题1. 原型对象2. 原型对象的this指向3. 案例4. constructor属性5. 对象原型6. 总结7. 原型继承8. 原型链由先前的学习可知,构造函数实例创建的对象彼此独立、互不影响,很好的体现了面向对象…...
网络安全 2023 年为什么如此吃香?事实原来是这样....
前言由于我国网络安全起步晚,所以现在网络安全工程师十分紧缺。俗话说:没有网络安全就没有国家安全为什么选择网络安全?十四五发展规划建议明确提出建设网络强国,全面加强网络安全保障体系和能力建设,加强网络文明建设,…...

(源码篇02)webpack5中的事件调度系统和NormalModuleFactary核心逻辑
1. 书接上回,从 this.factorizeQueue.add(options, callback); 开始 不是很清楚上下文的兄弟,可以去看下我之前写的 (源码篇01)浅析webpack5中Compiler中重要的hook调用过程。 此文比较干,各位读者开始阅读前…...
做了啥?)
Vue2.x源码:new Vue()做了啥?
vue源码版本vue2.5.2 new Vue()做了啥? new Vue()会执行_init方法,而_init方法在initMixin函数中定义。 src/core/instance/index.js文件中定义了Vue function Vue (options) {this._init(options) }initMixin(Vue) stateMixin(Vue) eventsMixin(Vue) lifecycl…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
