聚类分析|距离与相似系数|层次聚类|K均值聚类|SPSS及Matlab
聚类分析问题描述
聚类分析问题描述
人类认识世界的方法之一就是将事物按照各种属性或特征分成若干类别。
物以类聚、人以群分。分类方法多种多样,简单直接的如高、矮、胖瘦。使用的信息量小,但对类别界限附近的案例,分类结果不一定合适。
为了满足更高的分类要求,对研究对象需用更多的特征变量来刻画。如要想把中国的县分类,就有多种方法,可以按照自然条件来分,比如考虑降水、土地、日照、湿度等,也可考虑收入、教育水准、医疗条件、基础设施等指标;既可以用某一项来分类,也可以同时考虑多项指标来分类。
引例:20种啤酒的热量、钠含量、酒精及价格四种变量。如何找到数据中隐藏的模式特征?
![![[Pasted image 20240822160347.png]]](https://i-blog.csdnimg.cn/direct/1fc4ec7c55c34401b2828f92ca699d25.png)
整理好的数据具有如下结构:
![![[Pasted image 20240822160424.png]]](https://i-blog.csdnimg.cn/direct/9c538f5d43ef4461ba2bcadf7acb3022.png)
x i x_{i} xi是特征变量,可能是分类变量(如民族、性别),也可能是数值变量(如
身高体重),单位量纲也不相同。每个对象用一个p维特征向量来刻画。
任意两各随机变量
X = ( x 1 , x 2 , … , x n ) T , Y = ( y 1 , y 2 , … , y n ) T X=(x_{1},x_{2},\dots,x_{n})^{T},\ Y=(y_{1},y_{2},\dots ,y_{n})^{T} X=(x1,x2,…,xn)T, Y=(y1,y2,…,yn)T
的协方差
c o v ( X , Y ) = 1 n ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) cov(X, Y)=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y}) cov(X,Y)=n1i=1∑n(xi−xˉ)(yi−yˉ)
P维特征向量 ( X 1 , X 2 , … , X p ) (X_{1},X_{2},\dots,X_{p}) (X1,X2,…,Xp)的协方差矩阵
∑ = ( v ( x 1 ) c ( X 1 , X 2 ) … c ( X 1 , X p ) c ( X 1 , X 2 ) v ( X 2 ) … c ( X 2 , X p ) … … … … c ( X , X p c ( X 2 , X p ) … v ( X p ) ) \sum=\begin{pmatrix} v(x_{1})&&c(X_{1},X_{2})&&\dots&&c(X_{1},X_{p}) \\ c(X_{1},X_{2})&&v(X_{2})&&\dots&&c(X_{2},X_{p}) \\ \dots&&\dots&&\dots&&\dots \\ c(X,X_{p}&&c(X_{2},X_{p})&&\dots&&v(X_{p}) \end{pmatrix} ∑= v(x1)c(X1,X2)…c(X,Xpc(X1,X2)v(X2)…c(X2,Xp)…………c(X1,Xp)c(X2,Xp)…v(Xp)
聚类分析(clusteranalysis)就是基于数据自身信息来对数据进行分类的方法(也称为无监督学习)。
在聚类分析之前,研究者不知道观察对象可以分成多少个类,类的特点也无所得知。在分类的过程中,聚类分析能够从样本数据出发,自动进行分类。
不同研究者对于同一组数据进行聚类分析,所得到的聚类结果未必一致,因此聚类分析是一种探索性的分析方法。
聚类分析的数学描述
假设
X i = ( x i 1 , x i 2 , … , x i p ) , i = 1 , 2 , … n X_{i}=(x_{i1},x_{i2},\dots,x_{ip}),\quad i=1,2,\dots n Xi=(xi1,xi2,…,xip),i=1,2,…n
是待分析的对象全体。每个对象用p个特征变量来刻画。
聚类分析就是分析n个(对象)样本所对应的特征向量间的空间距离及分散情况,按照各样本间的距离远近或相似程度把n个样本划分成k个不相交非空的模式子集G1,G2,…,GK,称为簇或类,要求每一个样本能且只能隶属于某一类。
- 对研究样本聚类即数据表中的行作为对象,称为Q型聚类。
- 对特征变量(指标)进行聚类,即对数据中的列,对变量的聚类称为R型聚类。可以将一些相近的特征划归一类
它们在数学上是无区别的。
聚类分析的实质,就是结合研究目的、专业知识和数据特征,合理定义距离,把数据分成若干个类别,使得类别内部差异,尽可能小,类别间的差异尽可能大。
两种基本聚类算法
- HierarchicalCluster:谱系聚类或层次聚类
- K-Means Cluster:k-均值聚类法。
在聚类分析的前沿领域,有基于密度、基于网格和基于模型的新的聚类方法,本质上都是寻求更好的相似度(similarity)或距离的定义方法
距离与相似系数
如何在高维空间中度量距离远近呢?在啤酒数据中,每种饮料都有四个变量值。这就是四维空间点的距离了。
不仅要定义点和点之间的距离,也需要定义类(集合)和类(集合)之间的距离。不同距离定义方式影响聚类效果。
相似度是和距离相反但起同样作用的概态,两点相似度越大就相当于距离越短
两点间距离
给定任意两点
X = ( x 1 , x 2 , … , x p ) T , Y = ( y 1 , y 2 , … , y p ) T X=(x_{1},x_{2},\dots,x_{p})^{T},\ Y=(y_{1},y_{2},\dots,y_{p})^{T} X=(x1,x2,…,xp)T, Y=(y1,y2,…,yp)T
有多种方法定义两点间的距离
最常用的欧氏距离:
∑ i ( x i − y i ) 2 \sqrt{ \sum_{i} (x_{i}-y_{i})^{2}} i∑(xi−yi)2
欧氏距离的优点:几何意义明确,简单;
缺点:从统计意义上看,使用欧氏距离要求:
- 向量的p个分量互不相关具有相当的方差
- 各个坐标对欧氏距离的贡献同等且变差大小相同
也可采用欧氏距离平方
Minkowski距离:
( ∑ i = 1 p ∣ x i − y i ∣ q ) 1 / q \left( \sum_{i=1}^{p}| x_{i}-y_{i}|^{q} \right)^{1/q} (i=1∑p∣xi−yi∣q)1/q
当取q=1时,即为Block(绝对距离):
∑ i = 1 p ∣ x i − y i ∣ \sum_{i=1}^{p}| x_{i}-y_{i}| i=1∑p∣xi−yi∣
当q=o时,Chebychev距离:
m a x i ∣ x i − y i ∣ max_{i}| x_{i}-y_{i}| maxi∣xi−yi∣
缺点:
- 易受指标量纲的影响
- 未考虑指标间的相关性
B模距离
对于任意的正定矩阵B,由下式确定的距离称为B模距离
d X Y 2 = ( X − Y ) T B ( X − Y ) d^{2}_{XY}=(X-Y)^{T}B(X-Y) dXY2=(X−Y)TB(X−Y)
当B为单位矩阵时,即为欧式距离
若
B = d i a g ( 1 σ 1 2 , 1 σ 2 2 , … , 1 σ p 2 ) B=diag\left( \frac{1}{\sigma_{1}^{2}},\frac{1}{\sigma_{2}^{2}},\dots,\frac{1}{\sigma_{p}^{2}} \right) B=diag(σ121,σ221,…,σp21)
d X Y 2 = ( x 1 − y 1 ) 2 σ 1 2 + ( x 2 − y 2 ) 2 σ 2 2 + ⋯ + ( x p − y p ) 2 σ p 2 d_{XY}^{2}=\frac{(x_{1}-y_{1})^{2}}{\sigma_{1}^{2}}+\frac{(x_{2}-y_{2})^{2}}{\sigma_{2}^{2}}+\dots+\frac{(x_{p}-y_{p})^{2}}{\sigma_{p}^{2}} dXY2=σ12(x1−y1)2+σ22(x2−y2)2+⋯+σp2(xp−yp)2
当取协方差矩阵的逆矩阵时,得到马氏距离
Mahalanobis距离
B = [ c o v ( X ) ] − 1 = ∑ − 1 B=[cov(X)]^{-1}=\sum^{-1} B=[cov(X)]−1=∑−1
d X Y 2 = ( X − Y ) T ∑ − 1 ( X − Y ) d_{XY}^{2}=(X-Y)^{T}\sum^{-1}(X-Y) dXY2=(X−Y)T∑−1(X−Y)
优点:
- 排除了指标间的相关性干扰
- 不受指标量纲的影响
- 对原数据进行线性变换之后,马氏距离不变
相似系数
夹角余弦(Cosin)
d x y = cos θ x y = ∑ i x i y i ∑ i x i 2 ∑ i y i 2 , − 1 ≤ d x y ≤ 1 d_{xy}=\cos \theta_{xy}=\frac{\sum_{i}x_{i}y_{i}}{\sqrt{ \sum_{i}x_{i}^{2}\sum_{i}y_{i}^{2} }},\ -1\le d_{xy}\le 1 dxy=cosθxy=∑ixi2∑iyi2∑ixiyi, −1≤dxy≤1
相关系数(Pearson correlation)
d x y = γ x y = ∑ i ( x i − x ˉ ) ( y i − y ˉ ) ∑ i ( x i − x ˉ ) 2 ∑ i ( y i − y ˉ ) 2 d_{xy}=\gamma_{xy}=\frac{\sum_{i}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sqrt{ \sum_{i}(x_{i}-\bar{x})^{2}\sum_{i}(y_{i}-\bar{y})^{2} }} dxy=γxy=∑i(xi−xˉ)2∑i(yi−yˉ)2∑i(xi−xˉ)(yi−yˉ)
距离或相似度定义是聚类分析的关键步骤,要结合专业和所研究对象的特点设计。
比如Lance和Williams的距离
1 p ∑ i ∣ x i − y i ∣ x i + y i \frac{1}{p}\sum_{i} \frac{| x_{i}-y_{i}|}{x_{i}+y_{i}} p1i∑xi+yi∣xi−yi∣
兰氏距离是一个无量纲的量,克服了闵可夫斯基距离与各指标的量纲有关的缺点,且兰氏距离对大的奇异值不敏感,这使其特别适合高度偏移的和数据。但兰氏距离也没有考虑变量间的相关性。
再比如汉明距离(Hammingdistance):两个0,1字符码中不同位值的数目。
两类之间的距离
由一个点组成的类是最基本的类;如果每一类都由一个点组成那么点间的距离就是类问距离。但是如果某一类包含不止一个点,那么就要确定类间距离
类间距离是基于点间距离定义的:比如两类之间最近点之间的距离可以作为这两类之间的距离,也可以用两类中最远点之间的距离或各类的中心之间的距离来作为类间距离等。
给定两类 G p , G q G_{p},G_{q} Gp,Gq,及其均值中心 X p ˉ , X q ˉ \bar{X_{p}},\bar{X_{q}} Xpˉ,Xqˉ
两类之间的距离 D p q D_{pq} Dpq
最短距离法single
D p q = m i n X i ∈ G p , X j ∈ G q d ( x i , y j ) D_{pq}=min_{X_{i}\in G_{p},X_{j}\in G_{q}}d(x_{i},y_{j}) Dpq=minXi∈Gp,Xj∈Gqd(xi,yj)
最长距离法complete
D p q = m a x X i ∈ G p , X j ∈ G q d ( x i , y j ) D_{pq}=max_{X_{i}\in G_{p},X_{j}\in G_{q}}d(x_{i},y_{j}) Dpq=maxXi∈Gp,Xj∈Gqd(xi,yj)
重心法Centroid
D p q = d ( X p ˉ , X q ˉ ) D_{pq}=d(\bar{X_{p}},\bar{X_{q}}) Dpq=d(Xpˉ,Xqˉ)
类平均法average
D p q = 1 n 1 n 2 ∑ X i ∈ G p ∑ X j ∈ G q d ( X i , X j ) D_{pq}=\frac{1}{n_{1}n_{2}}\sum_{X_{i}\in G_{p}}\sum_{X_{j}\in G_{q}}d(X_{i},X_{j}) Dpq=n1n21Xi∈Gp∑Xj∈Gq∑d(Xi,Xj)
离差平方和Wald
D 1 = ∑ X i ∈ G p ( X i − X p ˉ ) ′ ( X i − X p ˉ ) D_{1}=\sum_{X_{i}\in G_{p}}(X_{i}-\bar{X_{p}})'(X_{i}-\bar{X_{p}}) D1=Xi∈Gp∑(Xi−Xpˉ)′(Xi−Xpˉ)
D 2 = ∑ X j ∈ G q ( X j − X q ˉ ) ′ ( X j − X q ˉ ) D_{2}=\sum_{X_{j}\in G_{q}}(X_{j}-\bar{X_{q}})'(X_{j}-\bar{X_{q}}) D2=Xj∈Gq∑(Xj−Xqˉ)′(Xj−Xqˉ)
D 1 + 2 = ∑ X ∈ G p ∪ G q ( X k − X ˉ ) ′ ( X k − x ˉ ) D_{1+2}=\sum_{X\in G_{p}\cup G_{q}}(X_{k}-\bar{X})'(X_{k}-\bar{x}) D1+2=X∈Gp∪Gq∑(Xk−Xˉ)′(Xk−xˉ)
⟹ D p q = D 1 + 2 − D 1 − D 2 \Longrightarrow D_{pq}=D_{1+2}-D_{1}-D_{2} ⟹Dpq=D1+2−D1−D2
G p ∪ G q G_{p}\cup G_{q} Gp∪Gq均值中心 X ˉ \bar{X} Xˉ。用两类合并后离差的增加量来衡量两类之间的距离
![![[Pasted image 20240822165548.png]]](https://i-blog.csdnimg.cn/direct/a16631f29d0f4b76904765404560d064.png)
![![[Pasted image 20240822165612.png]]](https://i-blog.csdnimg.cn/direct/d562c4145276416ca052e7aee3e401cc.png)
![![[Pasted image 20240822165619.png]]](https://i-blog.csdnimg.cn/direct/5dee5a1c4ea54de0b38bf67dfc1f32d0.png)
![![[Pasted image 20240822165644.png]]](https://i-blog.csdnimg.cn/direct/0826d7e69b6b4ad394314bdad7fc8ffd.png)
红绿合并(2,4,6,5)后的离差平方8.75
离差平方和增加8.75-2.5=6.25
黄绿合并(6,5,1,5)后的离差平方14.75
离差平方和增加14.75-8.5=6.25
黄红(2,4,1,5)后的离差平方
离差平方和增加10-10=0
故按该方法的连接和黄红首先连接。
层次聚类算法步骤及SPSS实现
层次聚类的方法原理
操作对象是类,
开始时,每一个样本点被看做一个类。
它首先把最近的两类(点)合并成一类,类数减少一个;
在剩下的类中继续寻找最近的两类合并;
这样下去,每次都少一类,直到最后只有一大类为止。越是后来合并的类,距离就越远。
聚类树的构造过程
- 计算n个样本点两两之间的距离,记为距离矩阵D
- 首先构造n个类,每个类只包含一个样本点,每一类的平台高度均为0
- 合并距离最近的两类为新类,并且以这两个类间的距离值作为聚类图中的平台高度
- 计算新类与当前各类的距离,调整距离矩阵。若类的个数等于1,转入步骤5,否则转到步骤3
- 画聚类图决定类的个数和类
以数据beer.sav为例,可以先通过菜单描述统计→描述→另存为变量将数据标准化。
![![[Pasted image 20240822171917.png]]](https://i-blog.csdnimg.cn/direct/61c27c1bc5f842c284a81c2f5decfe58.png)
然后选择菜单分析→分类→系统聚类。然后把标准化的热量、咖啡因、钠含量、价格选入变量框。
![![[Pasted image 20240822171831.png]]](https://i-blog.csdnimg.cn/direct/9b734bc500ec4ad4a3ba985cc0f3058f.png)
在方法按钮设置类间距离计算方法,如下图。
![![[Pasted image 20240822172017.png]]](https://i-blog.csdnimg.cn/direct/cdebffee6740444eab24ba17fabc9ab9.png)
在绘制按钮,选择画出树状图
![![[Pasted image 20240822172036.png]]](https://i-blog.csdnimg.cn/direct/21a3abd0cfbe4171a3f1d28063c6c566.png)
在平台高度发生较大跳跃的地方,可以提示最好的聚类数目。这里可以是2类或3类,选择聚成2类,并在保存按钮设置保存类成员
Cutoff=5,聚成了4类
Cutoff=12,聚成了2类
![![[Pasted image 20240822172323.png]]](https://i-blog.csdnimg.cn/direct/248df31ad56742b09703d2acd43b0b5c.png)
中间的系数,是两类合并时的距离,群集1,群集2和系数
这三列就是用矩阵表示的聚类树,合并过程
聚类分析要注意的问题
聚类分析是探索性研究,是一种描述统计方法,它没有深入的统计理论支持。可以试验不同的距离定义,不同的分类个数,以及使用原数据还是标准化数据等等。
聚类结果主要受所选择的变量影响。如果去掉一些变量,或者增加一些变量,结果会很不同。相比之下,聚类方法的选择则不那么重要了。
从应用角度讲,针对某个特定问题,很难得出一个完全确定,并且也有理论支持的结论。更多的时候,是依据聚类的结果在问题中的“有用性”来判断模型效果的好坏。
一个较好的聚类结果应该在类内样品尽可能相似的前提下,使得类的个数尽可能的少。
一个较好的聚类结果要有令人信服的解释。其中一个标准就是能不能给出可读性好的类别特征描述。
K均值聚类算法步骤及SPSS实现
K均值聚类的思想和算法
给定要聚类的数据点
X i = ( x i 1 , x i 2 , … , x i p ) , i = 1 , 2 , … , n X_{i}=(x_{i1},x_{i2},\dots,x_{ip}),i=1,2,\dots,n Xi=(xi1,xi2,…,xip),i=1,2,…,n
k-均值聚类算法中的k表示聚类的个数。事先并不知道,试探性给出或结合背景知识给出
每个类用一个中心点来表示。聚类中心点随机初始化。
C i , i = 1 , 2 , … , k C_{i},i=1,2,\dots ,k Ci,i=1,2,…,k
通过计算样本数据点与中心点距离,将所有样本数据点分配到距离最近的类中
∣ ∣ X i − C j ∣ ∣ , j = 1 , 2 , … , k | | X_{i}-C_{j}| |,j=1,2,\dots,k ∣∣Xi−Cj∣∣,j=1,2,…,k
K-均值聚类算法是一种迭代算法。每扫描一次就要重新计算每个聚类中心点的位置。当聚类中心点的位置变化在一定的阀值之内的时候停止变化时,最后就可以得到K个类,并且类中每个样本数据点到本簇的中心的距离都小于到其它簇中心的距离
主要的聚类过程有三步
- 随机生成k个初始点作为中心点。
- 将数据集中的数据按照距离中心点的远近,分配到各个类中。
- 将各个类中的数据求平均值,作为新的中心点,重复上一步,直到所有的簇不再改变。
![![[Pasted image 20240823043601.png]]](https://i-blog.csdnimg.cn/direct/8d6072ed9a194a8b89065b1f33311f29.png)
K均值聚类分析的SPSS实现
以数据Beer.sav为例,在SPSS中选择 分析→分类→k均值聚类
![![[Pasted image 20240823044959.png]]](https://i-blog.csdnimg.cn/direct/cfc05c00752f42b3a7f37d59874a880d.png)
然后把啤酒的热量、钠含量、酒精及价格选入变量框。
在聚类数目处选择2(自己试探可能的类数)。
如果想要知道哪种饮料分到哪类,则设置保存按钮,再选类成员。结果会写入数据表中。
![![[Pasted image 20240823044658.png]]](https://i-blog.csdnimg.cn/direct/8de7ed6f9b5b41f0b5cd573b1e2a5326.png)
利用SPSS,只迭代五次就达到目标了。这样就可以得到最后的三类的中心以及每类有多少点
![![[Pasted image 20240823044810.png]]](https://i-blog.csdnimg.cn/direct/c8310248bb304ddea616b81d10c728a1.png)
倒数第二列给出各类包含的样本。结果是:第一类为啤酒9、10、12、 16、19、20。剩下的饮料为第二类。最后一列给出到类中心的距离。
聚类分析MATLAB实现
两种聚类分析方法
一种是利用clusterdata函数对样本数据进行一次聚类,其缺点为可供用户选择的面较窄,不能更改距离的计算方法
另一种是分步聚类:
- 找到数据集合中对象两两之间的相似性或非相似性,用pdist函数计算变量之间的距离;
- 用linkage函数定义变量之间的连接;
- 用inconsistent函数评价聚类信息;
- 用cluster函数创建聚类。
pdist函数
调用格式:
Y = pdist(X, 'metric’)
说明:用metric指定的方法计算X数据矩阵中对象之间的距离。
- X:一个n×m的矩阵,它是由m个对象组成的数据集,每个对象的大小为n。
- metric指定距离计算方法:
euclid:欧氏距离(默认)
seuclid:标准化欧氏距离
mahal:马氏距离;等等
linkage函数
调用格式:
Z = linkage(Y, 'method')
说明:用method参数指定的算法计算系统聚类树
返回:
- Z,为一个包含聚类树信息的(n-1)×3的矩阵。记载系统聚类合并过程。
- Y,pdist函数返回的距离矩阵;
- method:可取值如下:
single:最短距离法(默认);
complete:最长距离法;
average:未加权平均距离法:
weighted:加权平均法;
centroid:质心距离法;
median:加权质心距离法;
ward:内平方距离法(最小方差算法)
dendrogram函数
调用格式:
[H, T, ...] = dendrogram(Z, p,...)
说明:生成只有顶部p个节点的谱系图
inconsistent函数
说明:利用linkage函数生成的Z,计算两个节点合并时的不一致性。
调用格式:
c = inconsistent(Z)
cluster函数
Cluster(Z,a)
其中0<a<2,表示linkage输出的系统聚类树Z中距离小于a的样本点归于一类
·Cluster(Z,b)
其中b>1整数,表示将linkage输出的系统聚类树X分为b类
分布聚类步骤
- 寻找变量之间的相似性
最好先将数据用zscore函数进行标准化。
X2 = zscore(X); %标准化数据
Y2 = pdist(X2); %计算距离
- 定义变量之间的连接
Z2 = linkage(Y2);
- 评价聚类信息
C = inconsistent(Z2) %两个集合(节点)合并时的不一致度量
- 创建聚类,并作出谱系图
T = cluster(Z2,6); %这里聚6个类
H = dendrogram(Z2);
可直接调用clusterdata函数,根据数据创建分类调用格式:
T = clusterdata(X,...)
Clusterdata(x,a),其中0<a<2,表示将原始数据中距离小于a的样本点归于一类
Clusterdata(x,b),其中b>1整数,表示将原始数据x分为b类
T=clusterdata(X,cutoff)
与下面的一组命令等价:
Y = pdist(X, 'euclid');
Z = linkage(Y, 'single');
T = cluster(Z, cutoff);
MATLAB中若要实现k均值聚类,直接使用的K-means函数。
使用方法:
ldx = Kmeans(X, K)
[ldx, C] = Kmeans(X, K)
- X是NxP的数据矩阵
- K表示将X划分为几类,为整数
- C是KxP的矩阵,存储的是K个聚类质心位置,
- ldx Nx1的向量,存储的是每个点的聚类标号
相关文章:

聚类分析|距离与相似系数|层次聚类|K均值聚类|SPSS及Matlab
聚类分析问题描述 聚类分析问题描述 人类认识世界的方法之一就是将事物按照各种属性或特征分成若干类别。 物以类聚、人以群分。分类方法多种多样,简单直接的如高、矮、胖瘦。使用的信息量小,但对类别界限附近的案例,分类结果不一定合适。 …...
Linux中安装java和tomcat(保姆级教程)
java 篇 JDK是用于开发Java应用程序的软件开发工具包。它包含了编译器、调试器、运行时环境和其他一些开发工具,可以帮助开发人员创建、编译、调试和部署Java应用程序。JDK提供了Java编程语言的开发工具和运行时库,使开发人员能够编写和执行Java代码。 …...
Vue组件库Element和Vue路由
目录 一、Vue组件库Element(学会怎么CV) 快速入门 ElementUI的常用组件 1.Table表格 (1)组件演示 (2)组件属性详解 2.Pagination分页 (1)组件演示 (2࿰…...
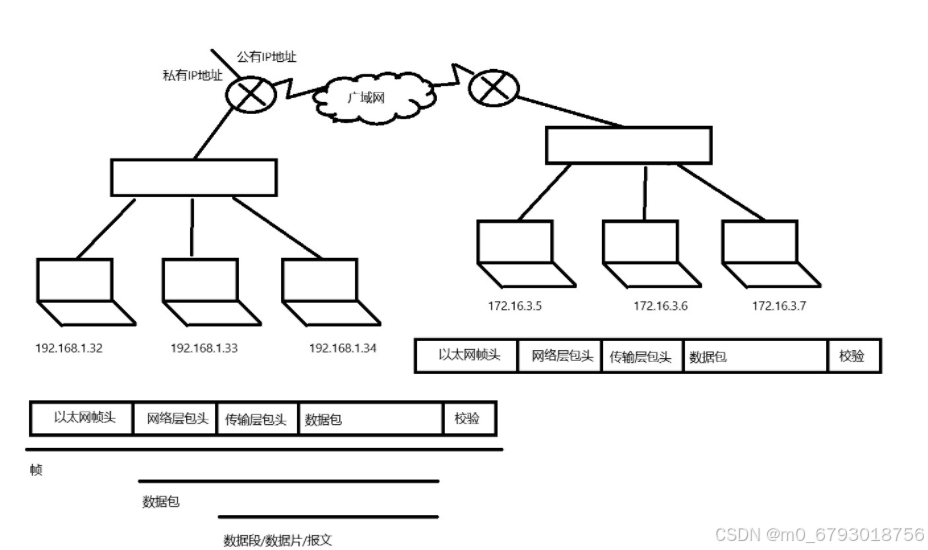
网络编程,网络协议,UDP编程
网络: 1.协议:通信双方约定的一套标准 2.国际网络通信协议标准: 1.OSI协议: 应用层 发送的数据内容 表示层 数据是否加密 会话层 是否建立会话连接 传输层 …...

通过访存地址获取主存数据的过程
目录 1.根据访存地址在Cache中查找数据 2.如果在Cache中命中 3.如果没有命中 4.数据送CPU 5.做几道题: 主要厘清思路,中间细节需自行补充! 1.根据访存地址在Cache中查找数据 ① 访存地址的结构会根据Cache和主存之间的映射方式不同而改变。映射方式…...
)
sqlite3交叉编译问题(对‘fcntl64@GLIBC_2.28’未定义的引用)
使用rk3568的编译器交叉编译程序,报如下错误: libsqlite3.so:对‘fcntl64GLIBC_2.28’未定义的引用 libsqlite3.so:对‘logGLIBC_2.29’未定义的引用在网上查了下这个问题的原因可能是在GLIBC库2.28版本中, "fcn…...
- 决策树模型)
每天一个数据分析题(四百九十六)- 决策树模型
回归树是可以用于回归的决策树模型,一个回归树对应着输入空间(即特征空间)的一个划分以及在划分单元上的输出值。以下哪个指标可用于回归树中的模型比较 A. Adjusted R2 B. F-measure C. AUC D. Precision & Recall 数据分析认证考试…...
七牛云 CDN 视频瘦身,为视频分发「减负增效」
随着智能设备的普及,以及各种以分享视频为主的平台的兴起,人们记录生活、分享故事的方式不再局限于文字和图片,而是越来越多地通过视频来表达。视频也不再需要复杂的制作过程,变得随手可得。 然而,视频在互联网上的爆炸…...

使用html-docx-js + fileSaver实现前端导出word
因为html-docx-js是16年的老库了,它代码里面用到的with语法现在严格模式不允许,用npm直接引入会报错,所以我们需要用其它方式引入 首先要将html-docx-js的代码放到项目中 html-docx-js/dist/html-docx.js at master evidenceprime/html-do…...

Spark2.x 入门:DStream 输出操作
在Spark应用中,外部系统经常需要使用到Spark DStream处理后的数据,因此,需要采用输出操作把DStream的数据输出到数据库或者文件系统中。 这里以《Spark2.1.0入门:DStream输出操作》中介绍的NetworkWordCountStateful.scala为基础…...

Python爬虫——简单网页抓取(实战案例)小白篇
Python 爬虫是一种强大的工具,用于从网页中提取数据。这里,我将通过一个简单的实战案例来展示如何使用 Python 和一些流行的库(如 requests 和 BeautifulSoup)来抓取网页数据。 实战案例:抓取一个新闻网站的头条新闻标…...
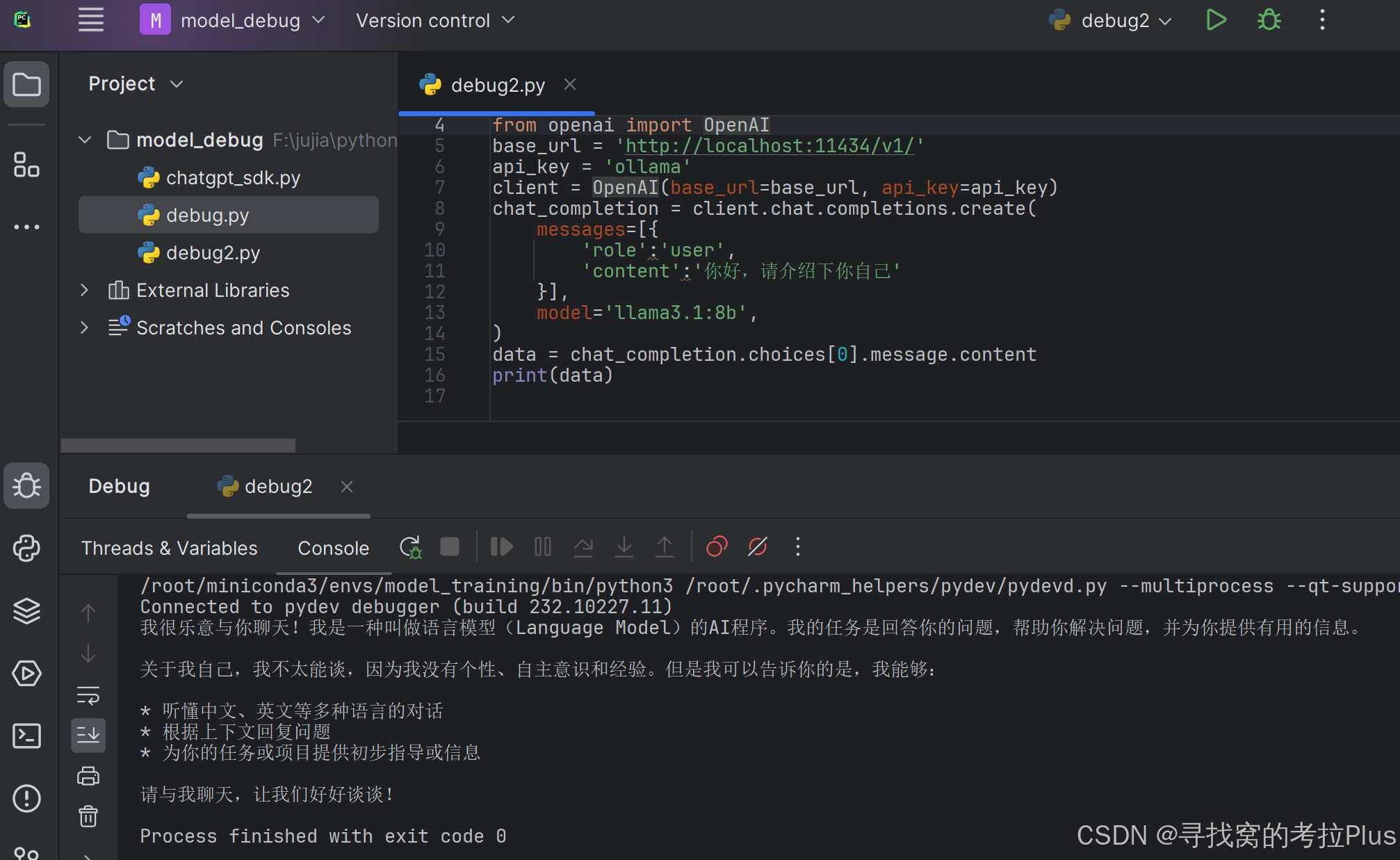
linux,ubuntu,使用ollama本地部署大模型llama3,模型通用,简易快速安装
文章目录 前言安装ollama启动ollama运行llama3模型查看ollama列表删除模型通过代码进行调用REST API 前言 在拥有了一条4090显卡后,那冗余的性能让你不得不去想着办法整花活,于是就想着部署个llama3,于是发现了ollama这个新大陆,…...

JS中的encodeURIComponent函数示例
JavaScript中的encodeURIComponent函数用于对字符串进行URL编码。它将字符串中的特殊字符转换为相应的编码形式,以确保字符串可以安全地嵌入到URL中。 使用encodeURIComponent函数时,它会将除了字母、数字、-、_、.、~以外的所有字符都进行编码。编码后…...

8.20 pre day bug
pre-bug1 分号省略 这些语句的分隔规则会导致一些意想不到的情形,如以下的一个示例; let m n f(bc).toString()但该语句最终会被解析为: let m n f(ab).toString();returntrue一定会被解析成 return;true;pre-bug2 Math.random()与Mat…...

位运算专题
分享丨【题单】位运算(基础/性质/拆位/试填/恒等式/思维) - 力扣(LeetCode) Leetcode 3133. 数组最后一个元素的最小值 我的答案与思路: class Solution { public: // 4 --> (100)2 7 --> (0111)2 // 5 --&g…...
)
HaProxy学习 —300K的TCP Socket并发连接实现(翻译)
HaProxy学习 —300K的TCP Socket并发连接实现(翻译) 1 原文链接2 原文翻译2.1 调整Linux系统参数2.2 调整HAProxy 1 原文链接 Use HAProxy to load balance 300k concurrent tcp socket connections: Port Exhaustion, Keep-alive and others࿰…...

92.WEB渗透测试-信息收集-Google语法(6)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:91.WEB渗透测试-信息收集-Google语法(5) 监控的漏洞也有很多 打…...
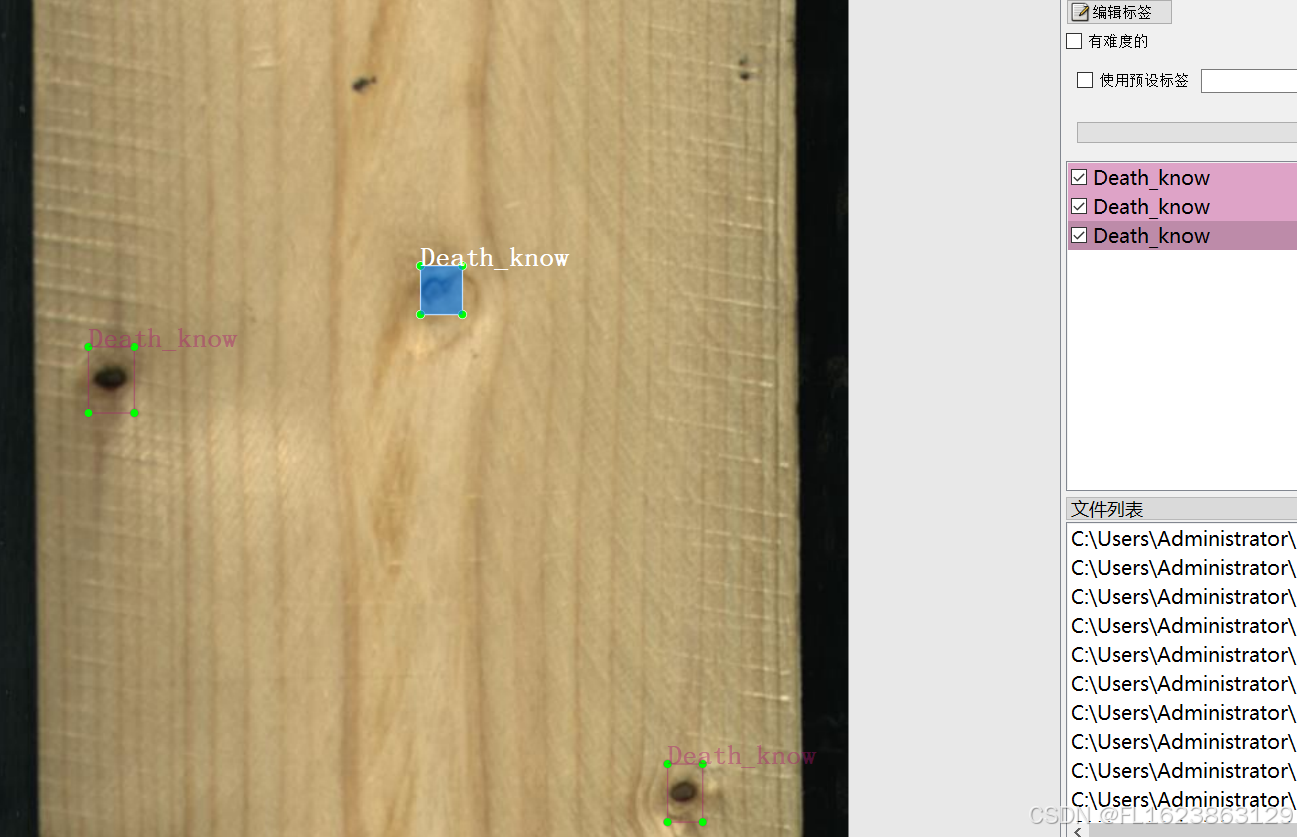
[数据集][目标检测]木材缺陷检测数据集VOC+YOLO格式2383张10类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):2383 标注数量(xml文件个数):2383 标注数量(txt文件个数):2383 标注…...

【启明智显分享】智能音箱AI大模型一站式解决方案重塑人机交互体验,2个月高效落地
2010年左右,智能系统接入音箱市场,智能音箱行业在中国市场兴起。但大潮激荡,阿里、小米、百度三大巨头凭借自身强大的资本、技术、粉丝群强势入局,形成三足鼎立态势。经过几年快速普及,智能音箱整体渗透率极高…...

逻辑与集合论基础及其在编程中的应用
目录 第一篇文章:逻辑与集合论基础及其在编程中的深度应用 引言 命题逻辑与谓词逻辑在编程中的深入应用 集合论及其在编程中的深度运用 函数的概念及其与集合的结合 总结与应用 第一篇文章:逻辑与集合论基础及其在编程中的深度应用 引言 逻辑与集…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
