CentOS上通过frp实现HTTPS访问内网
要在CentOS上通过frp实现HTTPS访问内网,你需要按照以下步骤操作:
-
在外网服务器上安装frps(frp服务端)。
-
在外网服务器上配置frps,编辑配置文件
frps.ini。 -
在frps服务器上启动frps服务。
-
在内网服务器上安装frpc(frp客户端)。
-
在内网服务器上配置frpc,编辑配置文件
frpc.ini。 -
在frpc服务器上启动frpc服务。
-
配置DNS或修改hosts文件,使得内网能够通过域名解析到外网服务器的IP。
-
通过域名进行HTTPS访问内网服务。
以下是简化的配置文件示例:
外网服务器(frps)的frps.ini配置:
[common]
bind_port = 7000内网服务器(frpc)的frpc.ini配置:
[common]
server_addr = <外网服务器的IP>
server_port = 7000[https_rule]
type = https
local_port = 443 # 内网服务器的HTTPS端口
custom_domains = <你的域名>确保你的域名指向外网服务器的IP,并且外网服务器的443端口(如果被防火墙限制,需要开放)能够接收来自frpc的流量。
启动frps(在外网服务器上):
./frps -c frps.ini启动frpc(在内网服务器上):
./frpc -c frpc.ini访问外网服务:
https://<你的域名>请确保你的域名已经正确解析到外网服务器的IP,并且外网服务器的安全组或防火墙规则允许相应的流量通过。如果你没有一个域名,你可以使用内网的IP地址或通过修改hosts文件来进行测试。
相关文章:

CentOS上通过frp实现HTTPS访问内网
要在CentOS上通过frp实现HTTPS访问内网,你需要按照以下步骤操作: 在外网服务器上安装frps(frp服务端)。 在外网服务器上配置frps,编辑配置文件frps.ini。 在frps服务器上启动frps服务。 在内网服务器上安装frpc&…...

短视频SDK解决方案,高效集成,助力商业变现
美摄科技,作为业界领先的多媒体技术服务商,其全面升级的短视频SDK解决方案,旨在为开发者与内容创作者提供一站式、高效能的创作工具,让每一个灵感都能瞬间转化为触动人心的视频作品。 【一站式解决方案,重塑短视频创作…...

C++系列-继承方式
继承方式 继承的语法继承方式:继承方式的特点继承方式的举例 继承可以减少重复的代码。继承允许我们依据另一个类来定义一个类,这使得创建和维护一个应用程序变得更容易。基类父类,派生类子类,派生类是在继承了基类的部分成员基础…...

web前端之选项卡的实现、动态添加类名、动态移除类名、动态添加样式、激活、间距、tabBar
MENU 原生(一)原生(二)vue(一) 原生(一) 效果图 html 代码 <div class"card"><div class"tab_bar"><div class"item" onclick"handleTabBar(this)">tabBar1</div><div class"item" onclick&qu…...

sql 优化,提高查询速度
文章目录 一、前言二、建议2.1 使用索引2.2 避免使用select *2.3. 使用表连接代替子查询2.4. 优化WHERE子句,减少返回结果集的大小2.5 用union all代替union2.6 使用合适的聚合策略2.7 避免在WHERE子句中使用函数2.8 使用EXPLAIN分析查询2.9 小表驱动大表2.10 使用窗…...

springboot后端开发-自定义参数校验器
背景 在使用springboot进行后端开发的时候,经常会遇到数据校验的问题, 有时候可能默认的校验器不足以满足自己的需求, 这个时候就需要开发一个自己的校验器 在 Spring Boot 中自定义参数校验器通常涉及以下几个步骤: 1. 定义注解…...
springboot社区帮扶对象管理系统论文源码调试讲解
第2章 开发环境与技术 社区帮扶对象管理系统的编码实现需要搭建一定的环境和使用相应的技术,接下来的内容就是对社区帮扶对象管理系统用到的技术和工具进行介绍。 2.1 MYSQL数据库 本课题所开发的应用程序在数据操作方面是不可预知的,是经常变动的&…...

EmguCV学习笔记 VB.Net 6.2 轮廓处理
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 EmguCV是一个基于OpenCV的开源免费的跨平台计算机视觉库,它向C#和VB.NET开发者提供了OpenCV库的大部分功能。 教程VB.net版本请访问…...
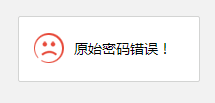
【Python的魅力】:利用Pygame实现游戏坦克大战——含完整源码
文章目录 一、游戏运行效果二、代码实现2.1 项目搭建2.2 加载我方坦克2.3 加载敌方坦克2.4 添加爆炸效果2.5 坦克大战之音效处理 三、完整代码 一、游戏运行效果 二、代码实现 坦克大战游戏 2.1 项目搭建 本游戏主要分为两个对象,分别是我方坦克和敌方坦克。用户可…...

【机器学习】经典CNN架构
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 经典CNN架构1. 引言2. LeNet3. AlexNet4. VGGNet5. GoogLeNet(Inception)6. Res…...

图像数据处理21
五、边缘检测 5.2基于二阶导数的边缘检测 一阶导数(如Sobel、Prewitt算子)能够捕捉到灰度值的快速变化,但有时会因检测到过多的边缘点而导致边缘线过粗。为了更加精确地定位边缘位置,可以利用二阶导数的零交叉点。零交叉点是是函…...

day37动态规划+三.Github链接本地仓库
一.动态规划 474.一和零 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。 思路:这道题更像是另一种的0-…...

设备运维故障排查与修复技巧
运维中最常见的40个故障问题及其解决方法: 1. 网络不通问题:无法访问网络资源。 解决方法:检查物理线路、交换机端口、网卡驱动和配置,使用ping、traceroute等工具定位问题。 2. 网络速度慢问题:访问网络资源速度慢。 解决方法:分析带宽使用情况,检查是否存在广播风…...

探索Python的自动化魔法:AutoIt库揭秘
文章目录 探索Python的自动化魔法:AutoIt库揭秘第一部分:背景介绍第二部分:AutoIt是什么?第三部分:如何安装AutoIt库?第四部分:AutoIt的五个简单函数第五部分:场景应用第六部分&…...

【I/O多路复用】
基于I/O多路复用的并发编程 I/O实现I/O多路复用select优缺点 pollepoll优点 I/O I/O复用是基于一个单进程或单线程的一个执行流当中监控多个输入输出流的技术(网络套接字或者文件描述符进行监控)。单进程或单线程,允许多个用户对单进程发起连…...

【python报错已解决】“IndexError: list index out of range”
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《C干货基地》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! 引言 你是否在处理Python列表时遇到了“IndexError: list index out of range”的错误?这个错误可能会让你的程序中…...

oracle和mysql查询某字段在哪个表中
oracle和mysql查询某字段在哪个表中 oracle的 select TABLE_NAME from user_tab_columns where COLUMN_NAME字段名mysql的: select table_schema ,table_name from information_schema.columns where column_name ‘字段名’ 查询结果table_schema为数据库名&a…...
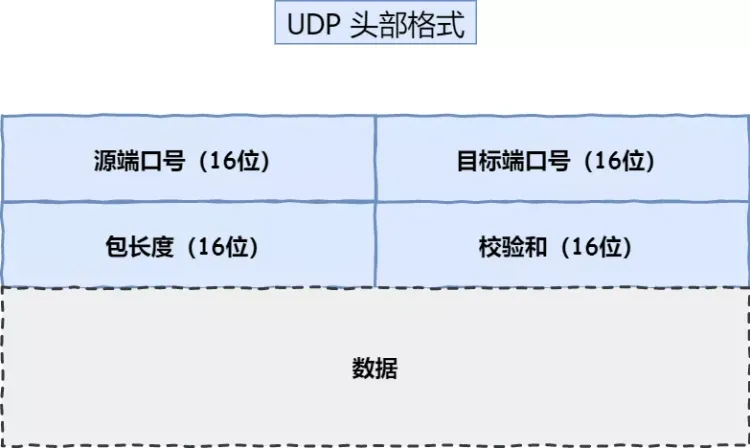
TCP vs UDP:揭秘可靠性与效率之争
概述 今天我们开始主要讲解TCP的相关知识点。在之前讲解分层章节的时候,我们提到过一个重要观点。在网络层及以下几层,更多的是让主机与主机建立连接,也就是说你的电脑需要知道另一台电脑在哪里才能连接上它。然而,在网络中的通信…...

“树”的高度的计算——CSP-J1真题详解
如同树有高度一样,数据结构中的“树”也有高度,只不过这个高度指的是第几“层”。就像武功可以修炼到第几层一样,树也可以长到第几层。 需要指明的是,树的根节点属于第几层是没有严格的定义的,一般被认为是处于第0层或…...

Docker介绍、docker安装以及实现docker的远程管理
1.Docker介绍 1.Docker介绍 Docker 是⼀个开源的应用容器引擎,可以实现虚拟化,完全采用“沙盒”机制,容器之间不会存在任何接口。 Docker 通过 Linux Container(容器)技术将任意类型的应用进行包装,变成一…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
