常用算法实现【必会】:sort/bfs/dfs
文章目录
- 常用排序算法实现(Go版本)
- BFS 广度优先遍历,利用queue
- DFS 深度优先遍历,利用stack
- 前序遍历(根 左 右)
- 中序遍历(左根右)
- 后序遍历(左 右 根)
- BFS/DFS 总结
常用排序算法实现(Go版本)
// 快排(分治)
// 时间复杂度:O(nlogn) 空间复杂度:O(logn)
func QuickSort(arr []int, left, right int) {var QuickSorting = func(arr []int, left, right int) int {tmp := arr[right] // 1、从右向左依次选基准值tmpfor left < right {for arr[left] <= tmp && left < right { // 2、每轮循环中先从左向右,遇到比基准值小的数则left++left++}if left < right {arr[right] = arr[left] // 3、直至遇到比基准值大的数x=array[left]为止,然后再交换基准值与较大值x的位置(保证基准值左侧的值都比基准值tmp小)}for arr[right] >= tmp && left < right { // 4、每轮循环中再从右向左,遇到比基准值大的数则right--right--}if left < right { // 5、直至遇到比基准值小的数y=array[right]为止,然后再交换基准值与较小值y的位置(保证基准值右侧的值都比基准值tmp大)arr[left] = arr[right]}}arr[left] = tmpreturn left}if left < right {mid := QuickSorting(arr, left, right)QuickSort(arr, left, mid-1)QuickSort(arr, mid+1, right)}
}// 快排(非递归)// todo:待补充
// https://www.bilibili.com/video/av758822583/?vd_source=2c268e25ffa1022b703ae0349e3659e4
func QuickSortNotByRecursion(arr []int) {
}// 堆排(大顶堆:每个节点的值都大于或等于其左右孩子节点的值)
// 时间复杂度:O(nlogn) 空间复杂度:O(1)
func HeapSort(arr []int) {var CreateHeap = func(arr []int, i, length int) {tmp := arr[i]// 注意for循环条件:是 j<length 而不是 j<len(arr)for j := 2*i + 1; j < length; j = j*2 + 1 { // j=2i+1:当前根节点的左孩子下标 j= 2*j + 1:以当前叶子节点为新根节点,该新根节点的下一层叶子节点左孩子下标if j+1 < length && arr[j] < arr[j+1] { // j+1<length:右孩子(j+1)不能超出len长度范围j++}if tmp > arr[j] { // 左右孩子节点中选较大的节点值,并与父节点比较大小break // 若父节点值满足"大于或等于其左右孩子节点的值"则break,否则与较大的孩子节点相互交换}arr[i] = arr[j]i = j}arr[i] = tmp // 将最终比较后较小值放到合适的位置}// 首次构建堆l := len(arr)for i := l / 2; i >= 0; i-- { // 从二叉树最后一个父节点从底向上遍历(最上面的父节点:i = 0;最后一个父节点下标:i = len(arr) / 2)CreateHeap(arr, i, l)}// 再次重建堆for i := l - 1; i > 0; i-- { // 从下往上不断在每轮循环中置换出当前最大值,arr长度i也逐渐减到0arr[0], arr[i] = arr[i], arr[0] // swap 把大顶堆根节点(下标为0)上的最大值交换到末尾,置换出来.CreateHeap(arr, 0, i)}
}// 归并
// 时间复杂度:O(nlogn) 空间复杂度:O(n)
func MergeSort(arr []int, length int) {var MergeSorting = func(arr1, arr2 []int, length1, length2 int) {i, j := 0, 0tempArr := make([]int, 0 /*, length1+length2*/)// 1.分别将两个子数组中较小一方的值按大小顺序移动到临时数组tempArr中for i < length1 && j < length2 {if arr1[i] < arr2[j] {tempArr = append(tempArr, arr1[i]) // 将较小值加入临时数组tempArri++// fmt.Println("i ", i)} else {tempArr = append(tempArr, arr2[j])j++// fmt.Println("j ", j)}}// 2.肯定存在一个子数组先移动完,所以需要将另一个未移动完的有序子数组剩下的元素继续移动到tempArr中if i < length1 {tmpArr = append(tmpArr, arr1[i:]...)}if j < length2 {tmpArr = append(tmpArr, arr2[j:]...)}// 3.将合并数组值赋给原始数组copy(arr, tmpArr) // arr = tempArr // 此赋值方式不会影响main()中原数组arr中的值,仅仅在该函数作用域内的结果是排好序的// for i := 0; i < length1+length2; i++ {// arr[i] = tmpArr[i]// }}// 注意:下面的l1和l2不能写成 "len(arr)/2" 和 "len(arr)-l1"if length > 1 { // 最后拆至每个子数组只有一个元素l1 := length / 2l2 := length - l1arr1, arr2 := arr, arr[l1:] // arr1原数组前半部分、arr2原数组后半部分MergeSort(arr1, l1) // 不断拆分数组长度直至长度为1MergeSort(arr2, l2) // 不断拆分数组长度直至长度为1MergeSorting(arr1, arr2, l1, l2)// mid := length / 2// arr1, arr2 := arr[:mid], arr[mid:] // arr1原数组前半部分、arr2原数组后半部分// MergeSort(arr1, len(arr1)) // 不断拆分数组长度直至长度为1// MergeSort(arr2, len(arr2)) // 不断拆分数组长度直至长度为1// MergeSorting(arr1, arr2, len(arr1), len(arr2))}
}// 冒泡
// 时间复杂度:O(n^2) 空间复杂度:O(1)
func MaoPaoSort(arr []int) {for i := 0; i < len(arr); i++ {for j := i + 1; j < len(arr); j++ {if arr[i] > arr[j] {arr[i], arr[j] = arr[j], arr[i] // swap}}}
}func main() {array := []int{5, 28, 73, 19, 6, 0, 5}// MaoPaoSort(array)// QuickSort(array, 0, len(array)-1)// QuickSortNotByRecursion(array)// HeapSort(array)MergeSort(array, len(array))fmt.Println(array)return
}
BFS 广度优先遍历,利用queue
// BFS(利用队列:尾进头出)
func levelOrder(root *TreeNode) []int {res := make([]int, 0)if root == nil { return res}queue := []*TreeNode{root} // 开始循环前,先塞入rootfor len(queue) > 0 {root = queue[0] // 获取即将出队的头节点res = append(res, root.Val)queue = queue[1:] // 头结点出队if root.Left != nil {queue = append(queue, root.Left)}if root.Right != nil {queue = append(queue, root.Right)}}return res
}
DFS 深度优先遍历,利用stack
前序遍历(根 左 右)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
// 迭代
func preorderTraversal(root *TreeNode) []int {array := make([]int, 0)stack := make([]*TreeNode, 0)for root != nil || len(stack) > 0 {// 不断遍历左子树for root != nil {array = append(array, root.Val) // result, finally return stack = append(stack, root) // pushroot = root.Left}// 左子树遍历完了,开始从下往上遍历右子树(每次找栈顶指针,然后pop出栈)if len(stack) > 0 {root = stack[len(stack) - 1] // 获取栈顶元素root = root.Rightstack = stack[: len(stack) - 1] // pop}}return array
}// 递归
var array []int
func preorderTraversal(root *TreeNode) []int {array = make([]int, 0)dfs(root)return array
}func dfs(root *TreeNode) {if root == nil {return}array = append(array, root.Val)dfs(root.Left)dfs(root.Right)
}
中序遍历(左根右)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/// 迭代
func inorderTraversal(root *TreeNode) []int {res := make([]int, 0)stack := make([]*TreeNode, 0)for root != nil || len(stack) > 0 {for root != nil {stack = append(stack, root)root = root.Left}if len(stack) > 0 {top := stack[len(stack) - 1]res = append(res, top.Val)root = top.Rightstack = stack[:len(stack) - 1] // pop}}return res
}// 递归
func inorderTraversal(root *TreeNode) []int {res := make([]int, 0)var inorder func(root *TreeNode)inorder = func(root *TreeNode) {if root != nil {inorder(root.Left)res = append(res, root.Val)inorder(root.Right)}}inorder(root)return res
}
后序遍历(左 右 根)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/// 迭代
// https://github.com/HelloWorld-666/C_Tree/blob/master/C_Tree/main.cpp
// 每个节点会经过两次栈,第一次不断遍历左子节点会经过,第二次遍历完右子节点后,获取栈顶节点时也会经过;
// 且当某个根节点root左右孩子节点都为空时,root出栈并置空
func postorderTraversal(root *TreeNode) []int {res := make([]int, 0)stack:= make([]*TreeNode, 0)flagMap := make(map[*TreeNode]int) // 标记节点是第几次经过根节点 => 入栈for root != nil || len(stack) > 0 {for root != nil { // 遍历左子节点stack = append(stack, root) // pushflagMap[root] = 1 // 第1次经过该节点时,做标记:1root = root.Left}if len(stack) > 0 {root = stack[len(stack) - 1] // 获取栈顶节点if flagMap[root] == 1 {flagMap[root] = 2 // 第2次经过该节点时,做标记:2root = root.Right} else {res = append(res, root.Val)stack = stack[:len(stack) - 1] // pop stack top noderoot = nil // 当前root的左右子节点都为空时(叶子节点),将该root出栈且置空,避免该root因不等于空而再次进入上方内循环中逻辑.}}}return res
}// 递归
func postorderTraversal(root *TreeNode) []int {res := make([]int, 0)var recursion func(root *TreeNode)recursion = func(root *TreeNode) {if root != nil {recursion(root.Left)recursion(root.Right)res = append(res, root.Val)}}recursion(root)return res
}
BFS/DFS 总结
将所有结点都看作根结点,关键在于何时访问。
前序:入栈时访问;中序:第一次退栈时访问;后序:第二次退栈时访问。
深度优先遍历(借助栈stack结构来实现) = 前中后序遍历
dfs:一条路走的死,用栈实现,进栈、退栈,一搜到底!一般用 递归 实现
bfs: 辐射八方,用队实现,入队、出队,步步为营!一般用 迭代 实现
深度优先,就是 一条路走到底,广度优先,就是 每条路都同时派人走 。
另外:删除一棵二叉树,即释放一棵二叉树的内存,用后序遍历即可实现(这里的“访问”变成了delete 结点).
相关文章:

常用算法实现【必会】:sort/bfs/dfs
文章目录常用排序算法实现(Go版本)BFS 广度优先遍历,利用queueDFS 深度优先遍历,利用stack前序遍历(根 左 右)中序遍历(左根右)后序遍历(左 右 根)BFS/DFS 总…...
瑟瑟发抖吧——用了这款软件,我的开发效率提升了50%
一、前言 开发中,一直听到有人讨论是否需要重复造轮子,我觉得有能力的人,轮子得造。但是往往开发周期短,用轮子所节省的时间去更好的理解业务,应用到业务中,也能清晰发现轮子的利弊,一定意义上…...
笔记本只使用Linux是什么体验?
个人主页:董哥聊技术我是董哥,嵌入式领域新星创作者创作理念:专注分享高质量嵌入式文章,让大家读有所得!近期,也有朋友问我,笔记本只安装Linux怎么样,刚好我也借此来表达一下我的感受…...

pipeline业务发布
业务环境介绍公司当前业务上线流程首先是通过nginx灰度,dubbo-admin操作禁用,然后发布上线主机,发布成功后,dubbo-admin启用,nginx启用主机;之前是通过手动操作,很不方便,本次优化为…...

【巨人的肩膀】JAVA面试总结(七)
💪MyBatis 1、谈谈你对MyBatis的理解 Mybatis是一个半ORM(对象关系映射)框架,它内部封装了JDBC,加载驱动、创建连接、创建statement等繁杂的过程,开发者开发时只需要关注如何编写SQL语句,可以…...

Python满屏表白代码
目录 前言 爱心界面 无限弹窗 前言 人生苦短,我用Python!又是新的一周啦,本期博主给大家带来了一个全新的作品:满屏表白代码,无限弹窗版!快快收藏起来送给她吧~ 爱心界面 def Heart(): roottk.Tk…...
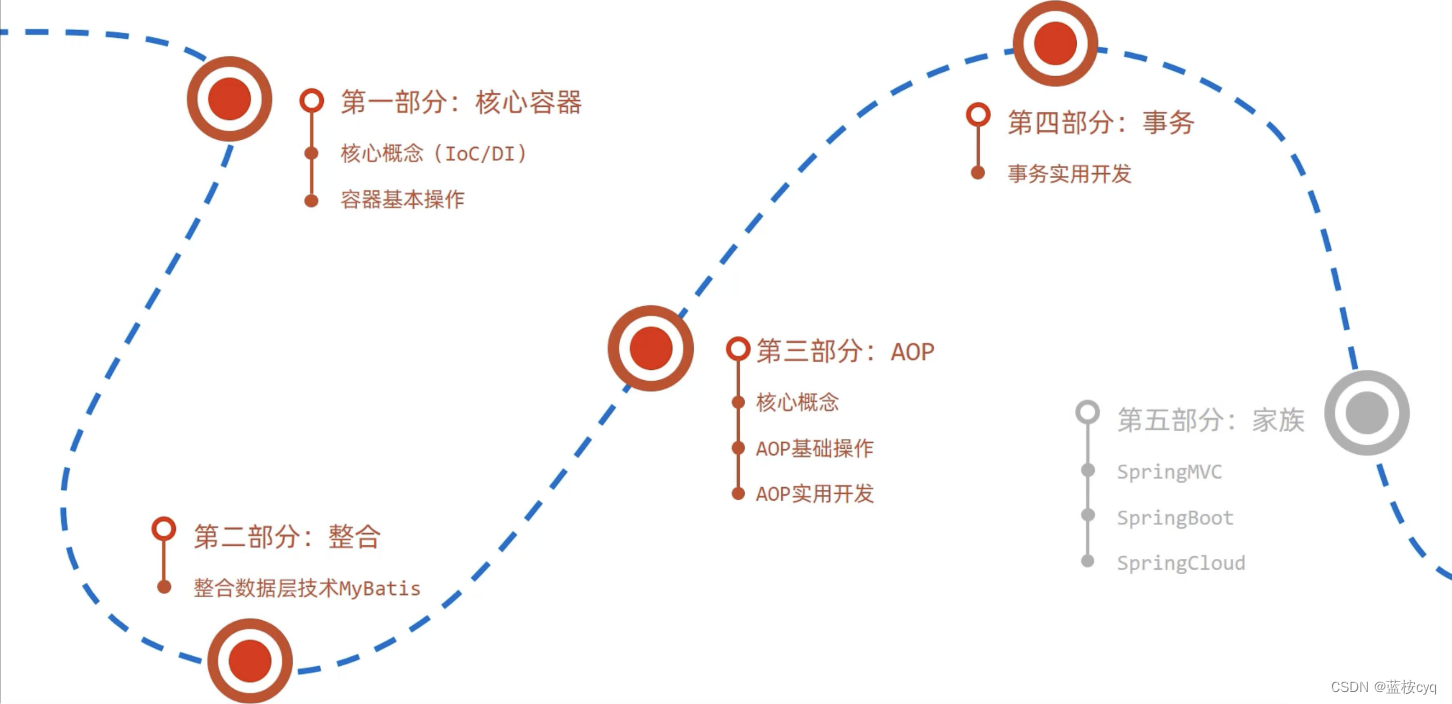
Spring学习流程介绍
Spring学习流程介绍 Spring技术是JavaEE开发必备技能,企业开发技术选型命中率>90%; Spring有下面两大优势: 简化开发: 降低企业级开发的复杂性 框架整合: 高效整合其他技术,提高企业级应用开发与运行效率 Spring官网: https://spring.io/ Spring发展…...
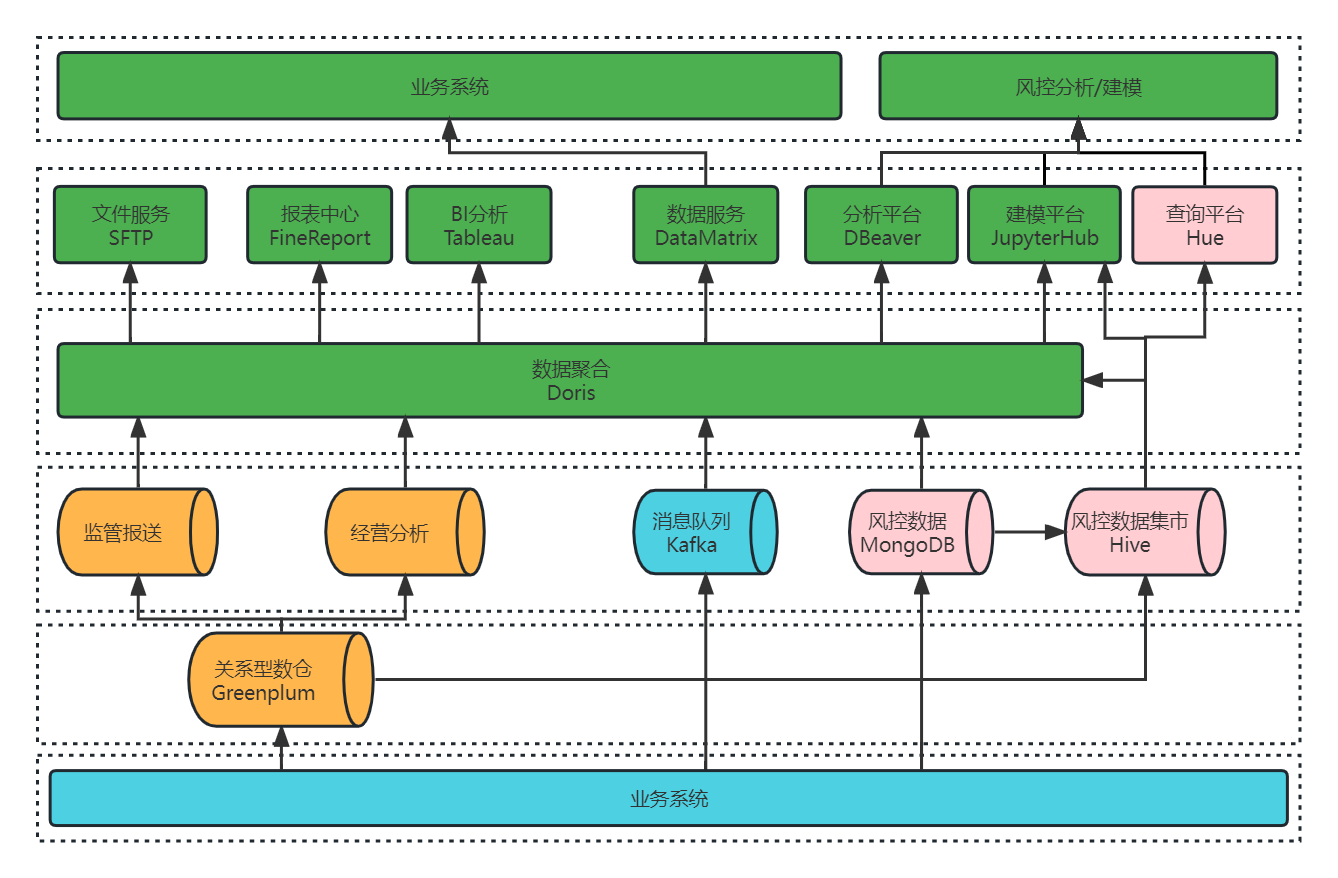
杭银消金基于 Apache Doris 的统一数据查询网关改造
导读: 随着业务量快速增长,数据规模的不断扩大,杭银消金早期的大数据平台在应对实时性更强、复杂度更高的的业务需求时存在瓶颈。为了更好的应对未来的数据规模增长,杭银消金于 2022 年 10 月正式引入 Apache Doris 1.2 对现有的风…...
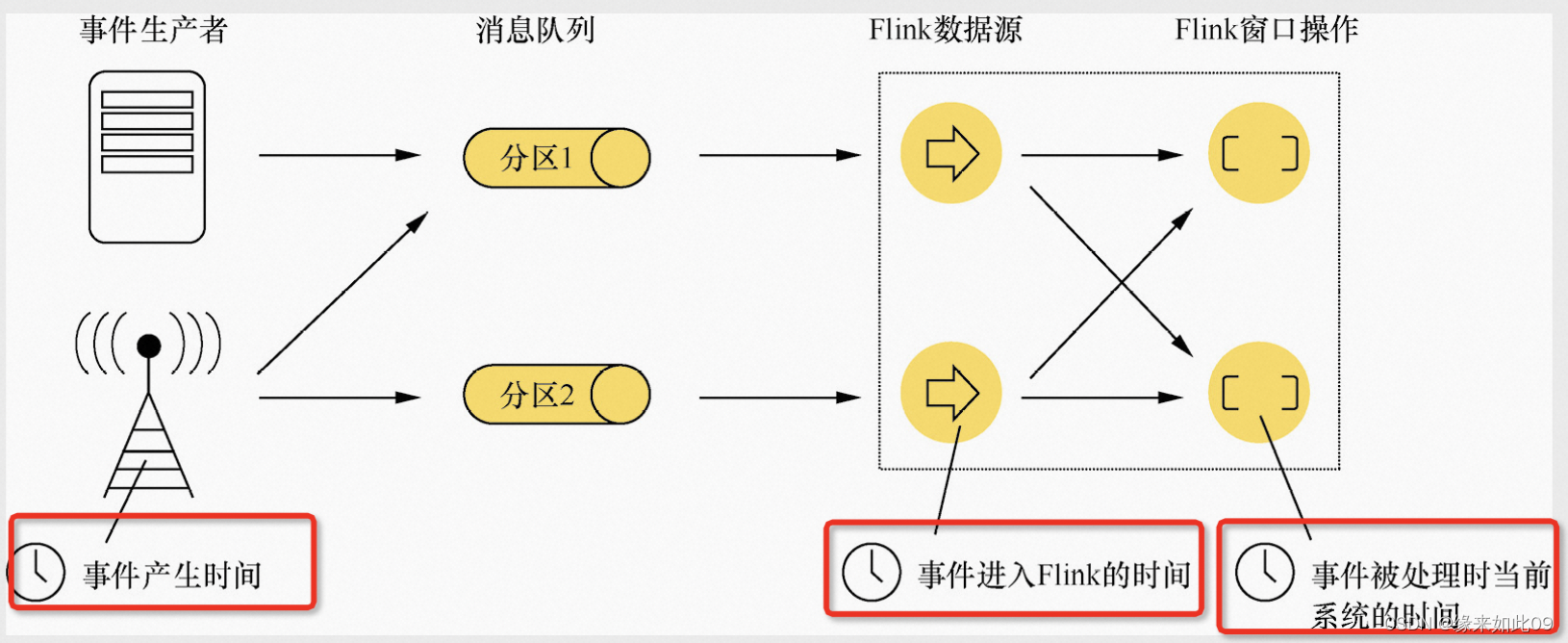
Flink学习笔记(六)Time详解
一、Flink中Time的三种类型: Stream数据中的Time(时间)分为以下3种: 1.Event Time(事件产生的时间): 事件的时间戳,通常是生成事件的时间。Event time 是事件本身的时间,…...

「Vue面试题」在项目中你是如何解决跨域的?
文章目录一、跨域是什么二、如何解决CORSProxy一、跨域是什么 跨域本质是浏览器基于同源策略的一种安全手段 同源策略(Sameoriginpolicy),是一种约定,它是浏览器最核心也最基本的安全功能 所谓同源(即指在同一个域&…...
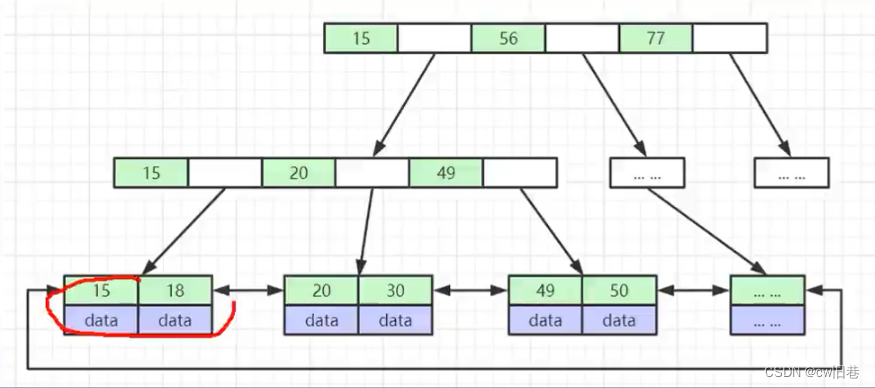
java八股文--数据库
数据库1.索引的基本原理2.聚簇和非聚簇索引的区别3.mysql索引的数据结构以及各自的优劣4.索引的设计原则5.事务的基本特性和隔离级别6.mysql主从同步原理7.简述MyISAM和InnoDB的区别8.简述mysql中索引类型及对数据库性能的影响9.Explain语句结果中各个字段分别表示什么10.索引覆…...

vue中名词解释
No名称略写作用应用场景其他1 单页面应用 (Single-page application) SPA 1,控制整个页面 2,抓取更新数据 3,无需加载,进行页面切换 丰富的交互,复杂的业务逻辑的web前端一般要求后端提供api数据…...

基于Java+SSM+Vue的旅游资源网站设计与实现【源码(完整源码请私聊)+论文+演示视频+包运行成功】
博主介绍:专注于Java技术领域和毕业项目实战 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟 Java项目精品实战案例(200套) 目录 一、效果演示 二、…...
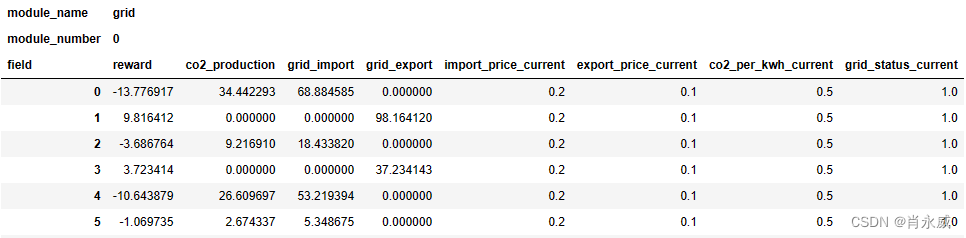
用于人工智能研究的开源Python微电网模拟器pymgrid(入门篇)
pymgrid是一个开源Python库,用于模拟微型电网的三级控制,允许用户创建或自行选择的微电网。并可以使用自定义的算法或pymgrid中包含的控制算法之一来控制这些微电网(基于规则的控制和模型预测控制)。 pymgrid还提供了与OpenAI Gy…...
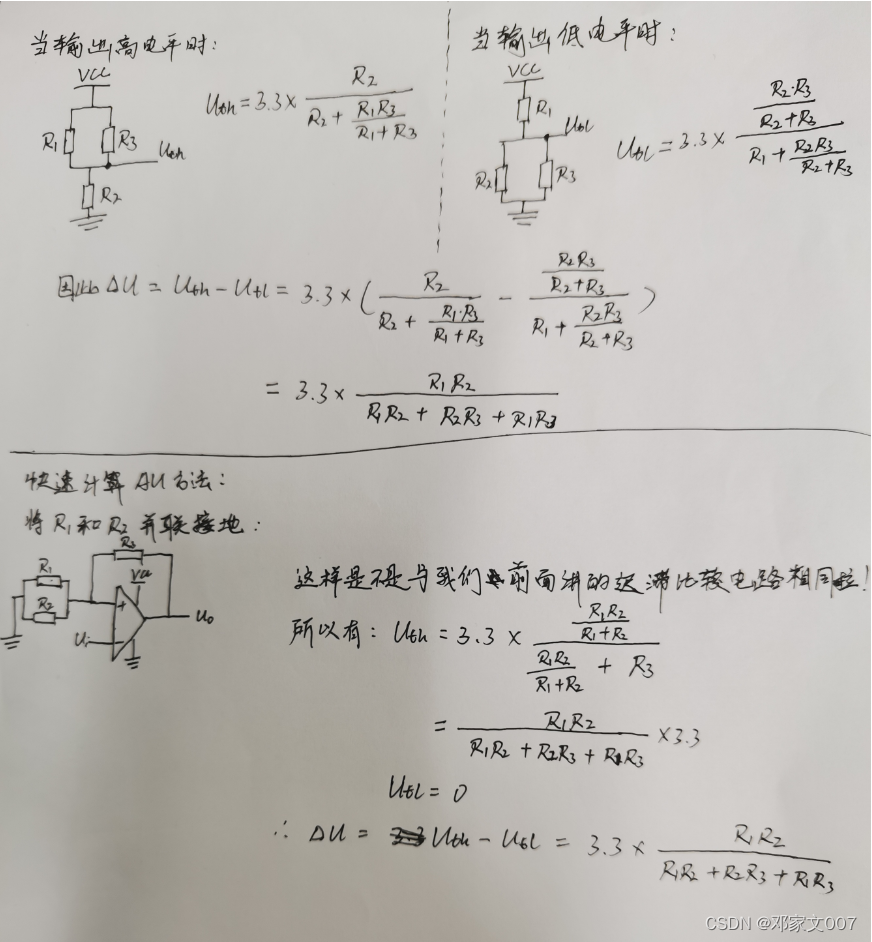
运算放大器:电压比较器、电压跟随器、同相比例放大器
目录一、单限电压比较器二、滞回电压比较器三、窗口电压比较器四、正点原子直流电机驱动器电路分析实战1、电压采集电路2、电流采集电路3、过流检测电路Ⅰ、采用分压后的输入电压:Ⅱ、采用理想电压源的输入电压:Ⅲ、同相输入电压采用的是非理想电压源&am…...

Vector - CAPL - 实时时间on *(续2)
继续继续。。。四、键盘事件这个键盘事件是我个人起的名字,为了方便与其他事件进行区分,为什么要把这一个单独拉出来说呢,因为它的用处实在是太广泛了,基本只要是使用CANoe做一些基本的自动化测试小工具,都会用到它&am…...

数据质量管理的四个阶段
然而,我们需要按照什么流程来对数据质量进行有效的管控,从而提升数据质量,释放数据价值?一般来讲,数据质量控制流程分为4个阶段:启动、执行、检查、处理。在管控过程中这4个阶段需不断循环,螺旋…...
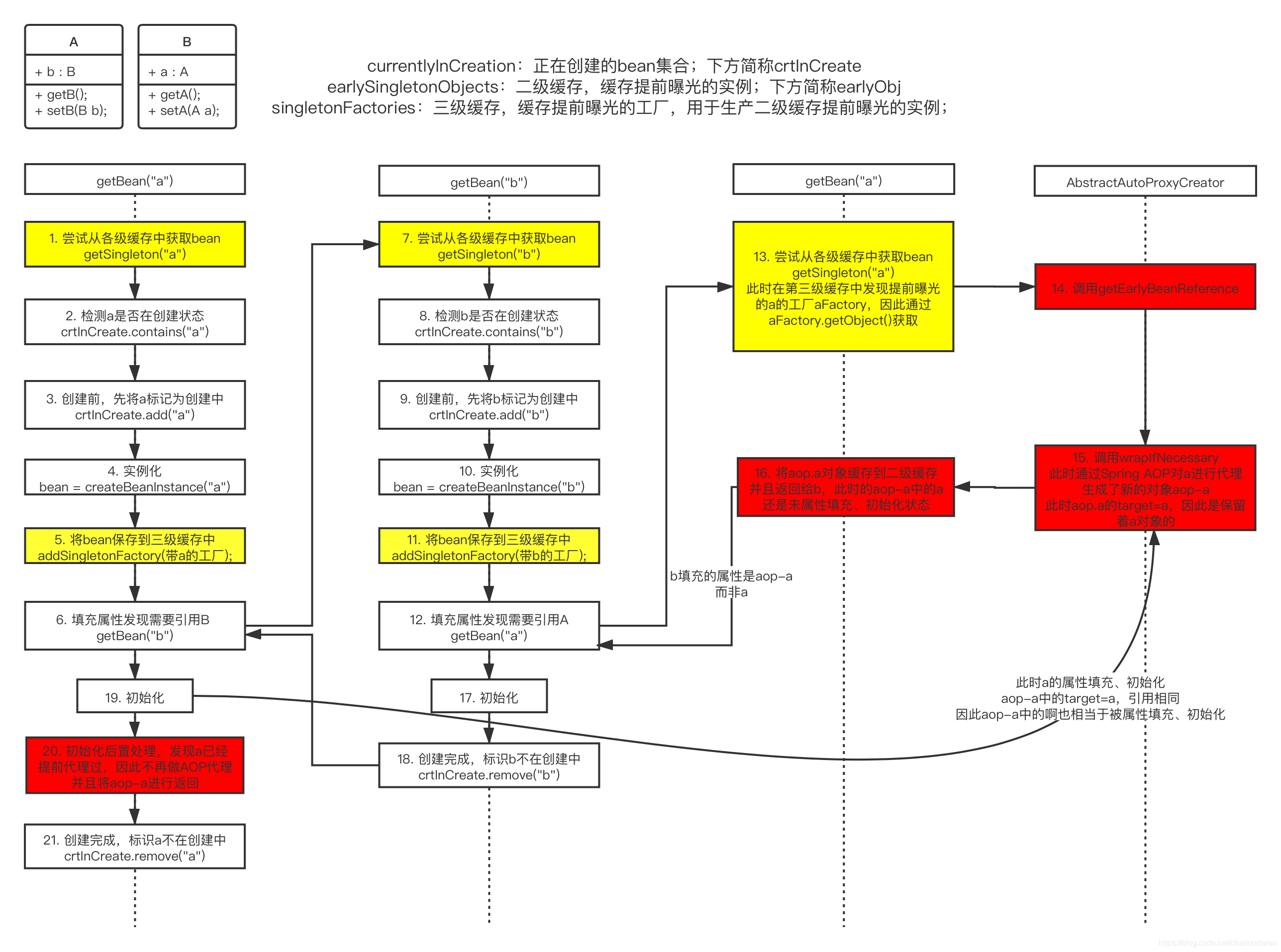
Spring源码面试最难问题——循环依赖
前言 问:Spring 如何解决循环依赖? 答:Spring 通过提前曝光机制,利用三级缓存解决循环依赖(这原理还是挺简单的,参考:三级缓存、图解循环依赖原理) 再问:Spring 通过提前…...
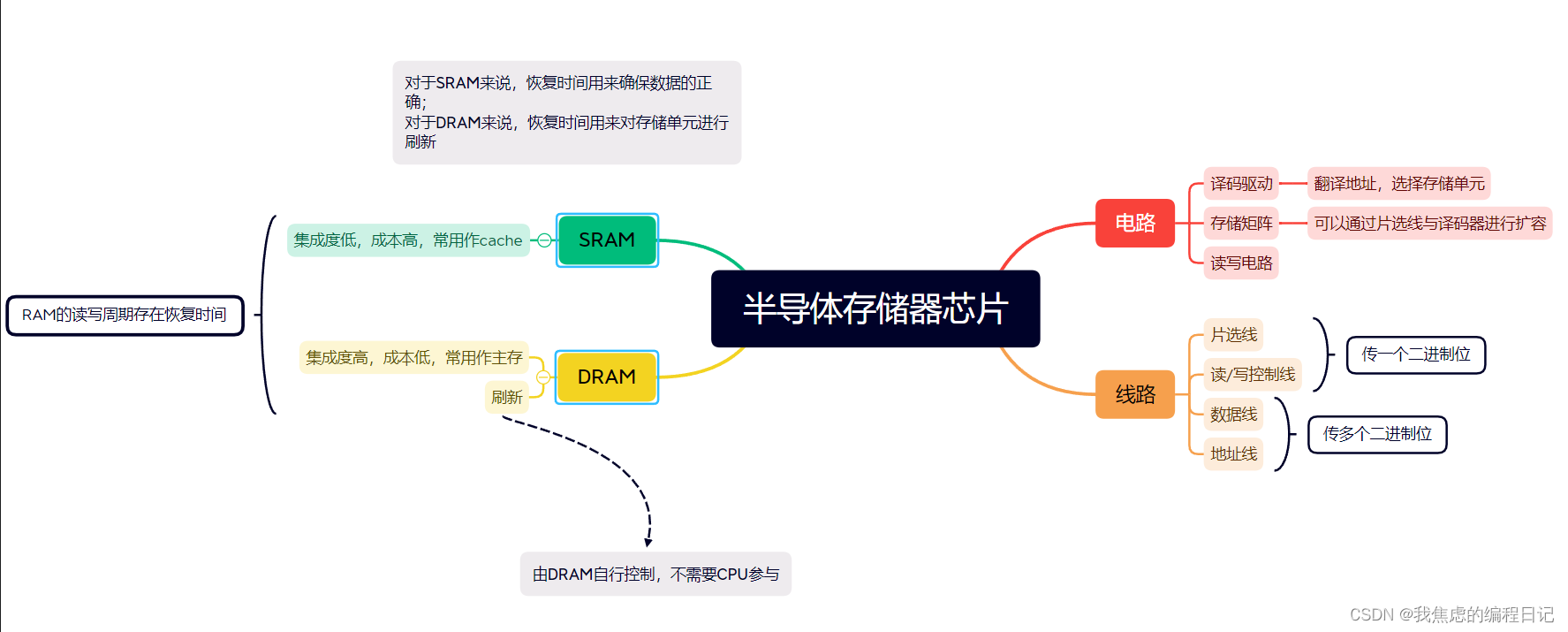
【计组】RAM的深入理解
一、存储机理 RAM的实现逻辑有种,分别是触发器和电容。 SRAM(Static)DRAM(Dynamic)存储方式触发器电容破坏性读出否(触发器具有稳态,能够锁住0或1两种状态)是(电容需要…...

JavaScript 之数据交互
在前后端交互中,前端通常需要对接口返回的数据进行格式转换、遍历、循环等;通常会用到以下函数和方法: forEach()、map()遍历数组(map返回新的数组);forEach()只能使用try catah终止循环;for in…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...
