数据结构实验1
实验题1:求1到n的连续整数和
题目描述
编写一个程序,对于给定的正整数n,求1+2+…十n,采用逐个累加与(n+1)/2(高斯法)两种解法。对于相同的n,给出这两种解法的求和结果和求解时间,并用相关数据进行测试。
运行代码
//实验题1:求1到n的连续整数和
#include<iostream>
#include<time.h>
#include<stdio.h>
#include<math.h>
using namespace std;
#define ll long long
ll add1(ll n) {ll sum = 0;for (ll i = 1; i <= n; i++) {sum += i;}return sum;
}
void AddTime1(ll n) {clock_t t;ll sum;t = clock();sum = add1(n);t = clock() - t;cout << "方法一:" << endl;printf(" 结果:1 到 %lld 之和:%lld\n", n, sum);printf(" 用时:%lf 秒\n", ((double)t) / CLOCKS_PER_SEC);
}
ll add2(ll n) {return n * (n + 1) / 2;
}
void AddTime2(ll n) {clock_t t;ll sum;t = clock();sum = add2(n);t = clock() - t;cout << "方法二:" << endl;printf(" 结果:1 到 %lld 之和:%lld\n", n, sum);printf(" 用时:%lf 秒\n", ((double)t) / CLOCKS_PER_SEC);
}
int main() {ll n;printf("n(大于 1000000):");cin >> n;if (n < 1000000) return 0;AddTime1(n);AddTime2(n);return 0;
}代码思路
- 头文件和命名空间
- 包含了必要的输入输出流头文件
<iostream>、时间相关头文件<time.h>、标准输入输出头文件<stdio.h>和数学库头文件<math.h>。 - 使用
using namespace std引入标准命名空间。 - 定义宏
ll为long long,方便后续使用长整型数据类型。
- 包含了必要的输入输出流头文件
- 函数定义
add1函数:使用循环遍历从 1 到n的整数,逐个累加求和。AddTime1函数:测量add1函数的执行时间,并输出结果和用时。add2函数:利用数学公式n*(n+1)/2直接计算从 1 到n的整数之和。AddTime2函数:测量add2函数的执行时间,并输出结果和用时。
main函数- 从用户输入获取整数
n,要求n大于 1000000,否则程序退出。 - 分别调用
AddTime1和AddTime2函数,对两种方法进行测试。
- 从用户输入获取整数
-
方法一的原理:循环遍历从 1 到
n的每个整数,逐个累加到变量sum中,最终得到从 1到n的整数之和。这种方法直观易懂,但当n较大时,循环执行次数较多,可能会比较耗时。 -
方法二的原理:利用数学公式
1 + 2 + 3 +... + n = n*(n+1)/2直接计算从 1 到n的整数之和。这个公式可以通过数学归纳法证明。这种方法避免了循环遍历,计算效率更高,尤其是对于较大的n。
通过测量两种方法的执行时间,可以看出当 n 较大时,方法二通常比方法一执行速度更快,因为方法二避免了大量的循环迭代操作,直接利用数学公式进行计算。
实验题2:常见算法时间函数的增长趋势分析
题目描述

运行代码
//实验题2:常见算法时间函数的增长趋势分析
#include <iostream>
#include <cmath>
using namespace std;
double log2(double n) {return log10(n) / log10(2);
}
int factorial(int n) {if (n == 0 || n == 1)return 1;elsereturn n * factorial(n - 1);
}
int main() {cout << "n\tlog2(n)\t√n\tn\tn^2\tn^3\t2^n\tn!" << endl;for (int n = 1; n <= 10; n++) {cout << n << "\t" << log2(n) << "\t" << sqrt(n) << "\t" << n << "\t" << n * n << "\t" << n * n * n << "\t" << pow(2, n) << "\t" << factorial(n) << endl;}return 0;
}代码思路
一、代码思路
- 函数定义
log2函数:通过换底公式logₐb = logₑb / logₑa,这里使用以 10 为底的对数函数log10计算出以 2 为底的对数。factorial函数:使用递归的方式计算给定整数n的阶乘。当n为 0 或 1 时,阶乘为 1;否则,n的阶乘等于n乘以n - 1的阶乘。
main函数- 首先输出表头,展示不同算法时间函数的名称。
- 使用循环从 1 到 10 遍历整数
n。 - 在循环中,分别计算并输出
n、以 2 为底n的对数、n的平方根、n、n的平方、n的立方、2 的n次方、n的阶乘的值。
二、原理
log2(n):对数函数的增长非常缓慢。随着n的增大,对数函数的值增长速度远远慢于线性增长。√n:平方根函数的增长速度比线性增长慢,但比对数函数快。n:代表线性增长,即随着n的增加,函数值以相同的比例增加。n^2:二次函数的增长速度比线性增长快得多。当n增大时,二次函数的值增长迅速。n^3:三次函数的增长速度比二次函数更快。2^n:指数函数的增长速度非常快,远远超过其他函数。n!:阶乘函数的增长速度是所有这些函数中最快的。随着n的增大,阶乘函数的值呈爆炸式增长。
通过输出这些不同函数在不同n值下的结果,可以直观地观察到它们的增长趋势差异,对于分析算法的时间复杂度非常有帮助。例如,在选择算法时,如果一个算法的时间复杂度是指数级的(如2^n或n!),那么对于较大的输入规模,该算法可能会非常耗时,而如果算法的时间复杂度是线性的(如n)或对数级的(如log2(n)),则通常会更加高效。
实验题3:求素数的个数
题目描述
编写一个程序,求1~n的素数个数。给出两种解法,对于相同的n,给出这两种解法的结果和求解时间,并用相关数据进行测试。
运行代码
//实验题3:求素数的个数
#include <iostream>
#include <ctime>
using namespace std;
bool isPrime1(int n) {// 方法 1:传统方法判断素数,时间复杂度 O(n)if (n < 2) return false;for (int i = 2; i < n; i++) {if (n % i == 0) return false;}return true;
}
int prime1(int n) {int count = 0;for (int i = 2; i <= n; i++) {if (isPrime1(i)) count++;}return count;
}
bool isPrime2(int n) {// 方法 2:改进方法判断素数,时间复杂度 O(√n)if (n < 2) return false;if (n == 2 || n == 3) return true;if (n % 2 == 0 || n % 3 == 0) return false;for (int i = 5; i * i <= n; i += 6) {if (n % i == 0 || n % (i + 2) == 0) return false;}return true;
}
int prime2(int n) {int count = 0;for (int i = 2; i <= n; i++) {if (isPrime2(i)) count++;}return count;
}
void PrimeTime1(int n) {clock_t start = clock();int count = prime1(n);clock_t end = clock();double time_taken = double(end - start) / CLOCKS_PER_SEC;cout << "方法 1:1 到 " << n << " 的素数个数为 " << count << ",用时 " << time_taken << " 秒。" << endl;
}
void PrimeTime2(int n) {clock_t start = clock();int count = prime2(n);clock_t end = clock();double time_taken = double(end - start) / CLOCKS_PER_SEC;cout << "方法 2:1 到 " << n << " 的素数个数为 " << count << ",用时 " << time_taken << " 秒。" << endl;
}
int main() {int n;cout << "输入 n(n>100000):";cin >> n;PrimeTime1(n);PrimeTime2(n);return 0;
}代码思路
一、代码思路
- 函数定义
isPrime1函数:采用传统方法判断一个整数是否为素数。从 2 开始到该数减 1 进行遍历,如果存在能整除该数的数,则不是素数,否则是素数。时间复杂度为。prime1函数:利用isPrime1函数,遍历从 2 到n的所有整数,统计其中素数的个数。isPrime2函数:改进的方法判断素数。先处理特殊情况小于 2 的数、2 和 3。然后根据素数的性质,只需要判断到该数的平方根即可,并且只需要考虑 6 的倍数两侧的数(即i和i + 2),因为所有大于等于 5 的素数一定可以表示为 6k ± 1 的形式。时间复杂度为。prime2函数:与prime1类似,使用isPrime2函数遍历从 2 到n的整数,统计素数个数。PrimeTime1函数:测量prime1函数的执行时间,并输出素数个数和用时。PrimeTime2函数:测量prime2函数的执行时间,并输出素数个数和用时。
main函数- 提示用户输入一个大于 100000 的整数
n。 - 分别调用
PrimeTime1和PrimeTime2函数,对两种方法进行测试并输出结果。
- 提示用户输入一个大于 100000 的整数
二、原理
-
素数的定义:素数是指一个大于 1 的自然数,除了 1 和它自身外,不能被其他自然数整除。
-
两种判断素数方法的原理:
- 方法 1:传统方法通过遍历所有小于该数的整数来判断是否有能整除它的数。这种方法虽然直观,但效率较低,因为需要进行大量的除法运算。
- 方法 2:改进的方法利用了素数的分布规律。首先处理特殊情况,然后只需要判断到该数的平方根,并且只考虑特定形式的数,减少了不必要的判断,提高了效率。
-
统计素数个数的原理:通过遍历一定范围内的整数,对每个整数使用判断素数的函数进行判断,如果是素数则计数器加一。
-
测量执行时间的原理:使用
clock_t类型记录程序开始和结束的时间,通过计算时间差并除以CLOCKS_PER_SEC得到程序的执行时间,以秒为单位。
通过比较两种方法,可以看出在处理较大范围的素数个数计算时,改进后的方法(方法 2)具有更高的效率,因为其时间复杂度更低。
实验题4:求连续整数阶乘的和
题目描述
编写一个程序,对于给定的正整数n,求1!+2!+3!+…+n!。给出一种时间复杂度为O(n)的解法。
运行代码
//实验题4:求连续整数阶乘的和
#include <iostream>
using namespace std;
long long Sum(int n) {long long sum = 0;long long fact = 1;for (int i = 1; i <= n; i++) {fact *= i;sum += fact;}return sum;
}
int main() {int n;cout << "输入正整数 n(3-20):";cin >> n;if (n < 3 || n>20)return 0;long long result = Sum(n);cout << "1! + 2! + 3! +... + " << n << "! 的结果为:" << result << endl;return 0;
} 代码思路
一、代码思路
Sum函数:- 循环结束后,返回
sum,即从 1 到n的连续整数阶乘之和。 - 通过循环从 1 到
n遍历整数。在每次循环中,先将fact乘以当前的整数i,得到当前整数的阶乘,然后将这个阶乘累加到sum中。 - 初始化变量
fact为 1,用于存储当前整数的阶乘。 - 初始化变量
sum为 0,用于存储连续整数阶乘的和。
- 循环结束后,返回
main函数:- 提示用户输入一个正整数
n,要求在 3 到 20 之间。 - 如果输入的
n不在这个范围内,程序直接返回 0 退出。 - 调用
Sum函数计算从 1 到n的连续整数阶乘之和,并将结果存储在result中。 - 输出结果,显示从 1 到
n的连续整数阶乘之和的具体值。
- 提示用户输入一个正整数
二、原理
-
阶乘的定义:一个正整数的阶乘是所有小于及等于该数的正整数的乘积。例如,5 的阶乘是 5! = 5×4×3×2×1 = 120。
-
计算连续整数阶乘之和的原理:
- 通过循环依次计算每个整数的阶乘,并将其累加到总和中。
- 首先,初始化阶乘为 1,因为 1 的阶乘是 1。然后,从 2 开始,每次将当前整数乘以当前的阶乘得到新的阶乘,并将新的阶乘累加到总和中。
- 这样,通过循环可以依次得到 2!、3!、4!…… 直到
n!,并将它们累加到总和中,最终得到从 1! 到n!的连续整数阶乘之和。
相关文章:

数据结构实验1
实验题1:求1到n的连续整数和 题目描述 编写一个程序,对于给定的正整数n,求12…十n,采用逐个累加与(n1)/2(高斯法)两种解法。对于相同的n,给出这两种解法的求和结果和求解时间,并用相关数据进行测试。 运行代码 //实验题1:求1到n的连续整数和 #includ…...

使用Postman+JMeter进行简单的接口测试
以前每次学习接口测试都是百度,查看相关人员的实战经验,没有结合自己公司项目接口真正具体情况。 这里简单分享一下公司项目Web平台的一个查询接口,我会使用2种工具Postman和JMeter如何对同一个接口做调试。 准备工作 首先,登录公…...

基于 SpringBoot 的车辆充电桩管理系统
专业团队,咨询就送开题报告 摘 要 随着信息化时代的到来,管理系统都趋向于智能化、系统化,车辆充电桩管理系统也不例外,但目前国内仍都使用人工管理,市场规模越来越大,同时信息量也越来越庞大,…...
centos7.9安装clamav教程
本章教程主要记录在centos7.9安装clamav过程。 ClamAV(Clam AntiVirus)是一个开源的防病毒软件工具,主要用于检测和消除恶意软件。它最初由 Tomasz Kojm 于 2001 年开发,并由 Cisco Systems 维护和支持。ClamAV 广泛应用于邮件网关、文件服务器和其他需要防病毒保护的环境中…...

产品经理如何转型为AI产品经理,如何理解AI产品工程化
技术领域,特别是人工智能和机器学习,其优秀模型的成功应用是一个复杂过程,它不仅要求技术本身的卓越,还须与现有解决方案竞争,这涉及到技术成熟度、成本有效性、市场接受度等多维度因素。 在这一过程中,产品经理扮演着核心角色,负责协调各方利益,确保技术能够转化为满…...
TiDB从0到1学习笔记(精华篇)
历时四个月,恭喜赵老师的《TiDB从0到1》 系列文章顺利完结,小编再次梳理一遍文稿,并附注解分享给大家。 整体架构 从 TiDB 1.0 到 8.0,TiDB 的体系结构一直在不断演进。接下来让我们一起看看整体架构的变化。 TiDB v1 TiDB v1&…...
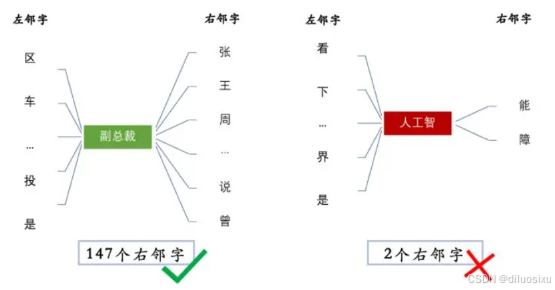
NLP-新词挖掘
一、背景 网络领域的新词发现(挖掘)是一个非常重要的nlp课题。在处理文本对象时,非常关键的问题在于“切词”这个环节,几乎所有的后续结果都依赖第一步的切词。因此切词的准确性在很大程度上影响着后续的处理,切词结果…...
电脑录屏不求人,9月必备免费录屏软件推荐!苹果电脑可用!
在当今这个信息爆炸的时代,电脑录屏软件已经成为了我们日常工作和生活中不可或缺的工具。无论是制作教学视频、录制在线课程、游戏直播,还是创建产品演示,一个好的录屏软件都能帮助我们更高效地完成任务。市场上的录屏软件琳琅满目࿰…...
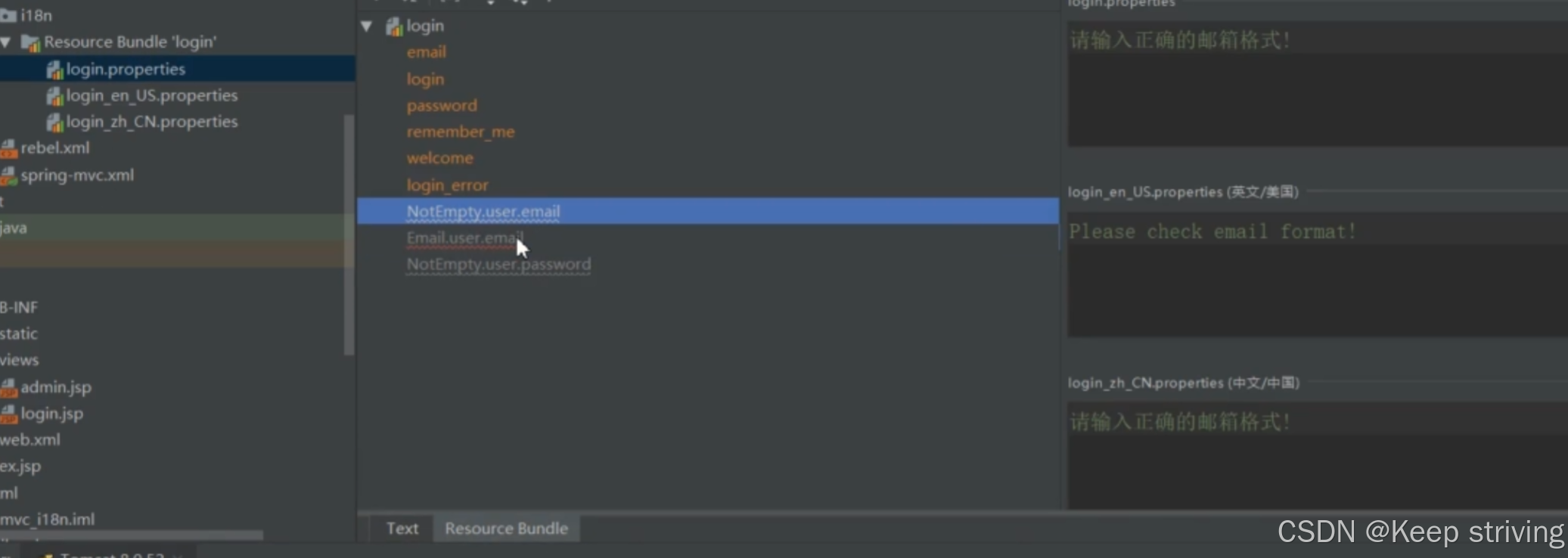
SpringMVC基于注解使用:国际化
01-国际化介绍 首先在bootstrap下载个页面 下载后把登录页面的代码粘上去 然后再登录页面代码上有些超链接需要再spring-mvc.xml里面配置下,登录页面才能正常显示 配置静态资源 国际化-根据浏览器语言国际化 现在是中文的情况,要改为英文 1.配置下属…...

工地安全帽检测系统源码分享
工地安全帽检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Computer V…...
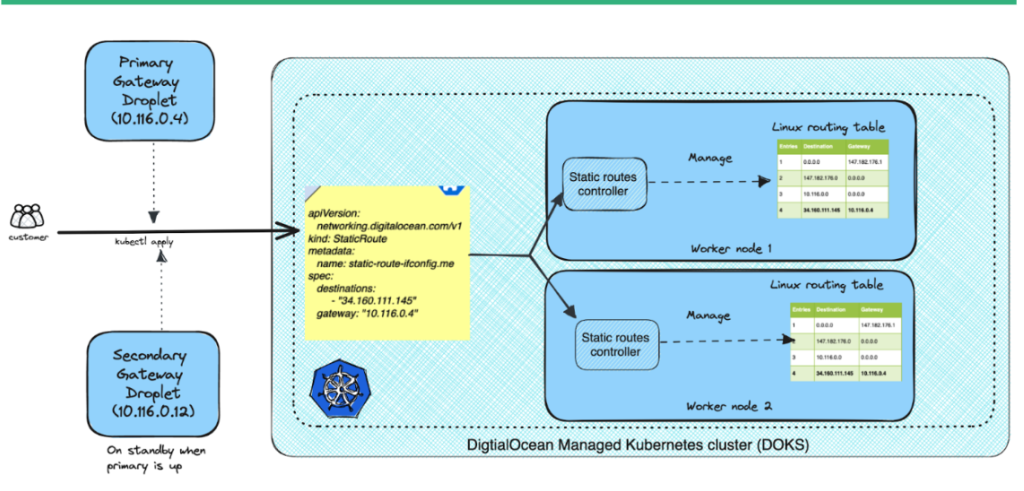
如何为 DigitalOcean 静态路由操作员设置故障转移
静态路由操作器的主要目的是提供更大的灵活性,并在 Kubernetes 环境中控制网络流量。它使你能够根据应用程序的需求自定义路由配置,从而优化网络性能。该操作器作为 DaemonSet 部署,因此将在你的 DigitalOcean Managed Kubernetes 集群的每个…...

Ansible简单部署与使用
目录 环境安装Ansibleapt installmarkupsafe error 配置Ansible创建个人目录ansible.cfghosts 测试Ansibleping批量执行自定义命令 环境 Ubuntu 20.04 安装Ansible apt install sudo apt install ansiblemarkupsafe error 安装成功后,尝试运行ansibleÿ…...

Harmony Next charles 抓包指南
1.选择安装移动证书 代理信息如下 2.设置手机代理 手机与电脑连接同一网络,然后配置步骤 1 的代理 路径:设置-wlan-选择当前网络编辑-代理-保存 注意:手机配置代理后,目前会默认断开连接,需要手动再连接下 wifi 3.鸿…...

【HarmonyOS】Beta最新对外版本IDE下载和环境配置
【HarmonyOS】Beta最新对外版本IDE下载和环境配置 前言 目前华为HarmonyOS的系统版本已经从Develop Beta升级为Beta预览版,全面开放。再也不需要白名单限制,才能下载使用最新的IDE和预览最新的开放文档了。 IDE下载和安装 Beta IDE下载地址 1.根据你…...

2024年9月第2周AI资讯
阅读时间:3-4min 更新时间:2024.9.9-2024.9.13 目录 Groq推出多模态大模型LLaVA v1.5 7B AI通过重读问题可以变得更聪明 美国Weave公司发布Isaac多功能个人机器人 特斯拉机器人出租车将实现无线充电 Adobe视频编辑新时代 无人驾驶汽车超越人类 AI…...

【软件使用-MEGA】构建进化树报错
*_summary.txt报错: MEGA-CC 10.2.6 Molecular Evolutionary Genetics Analysis Build#: 10210527-x86_640% Reading distance matrix MEGA-CC has logged the following error:When 2024年09月13日 下午 01时32分49秒 下午Data …...

面试常见八股
JAVA篇 基础 1、自动拆箱和装箱 装箱:装箱是将值类型(如int、double、struct等)转换为object类型或任何接口类型的过程。由于object是所有类型的基类(在.NET中),并且接口是引用类型,因此装箱…...

第十八章 番外 余弦相似度
余弦相似度(Cosine Similarity)是一种衡量两个非零向量之间角度的度量方式,用于评估它们之间的相似性。它的值范围从 -1 到 1,其中 1 表示完全相同的方向(即向量完全相同),0 表示正交࿰…...

HPA和helm
HPA pod的数量进行扩缩容 针对控制器创建的pod deployment: replica: 静态:edit yaml:apply -f HPA:基于cpu的利用率来实现pod数量的自动伸缩。 Horizontal pod autoscaling yaml文件————主流——————…...

基于人工智能的智能语音助手
语音助手的自然语言处理模块是语音助手系统的关键组成部分。通过这个模块,系统能够识别用户的意图并做出相应的回应。我们可以使用NLP技术来解析文本输入,并将其转换为系统可以理解的命令或指令。在本项目中,我们将结合语音识别、自然语言处理…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
