决策树ID3算法
1. 决策树ID3算法的信息论基础
机器学习算法其实很古老,作为一个码农经常会不停的敲if, else if, else,其实就已经在用到决策树的思想了。只是你有没有想过,有这么多条件,用哪个条件特征先做if,哪个条件特征后做if比较优呢?怎么准确的定量选择这个标准就是决策树机器学习算法的关键了。1970年代,一个叫昆兰的大牛找到了用信息论中的熵来度量决策树的决策选择过程,方法一出,它的简洁和高效就引起了轰动,昆兰把这个算法叫做ID3。下面我们就看看ID3算法是怎么选择特征的。
首先,我们需要熟悉信息论中熵的概念。熵度量了事物的不确定性,越不确定的事物,它的熵就越大。具体的,随机变量X的熵的表达式如下:
H(X)=−∑i=1npilogpiH(X) = -\sum\limits_{i=1}^{n}p_i logp_iH(X)=−i=1∑npilogpi
其中n代表X的n种不同的离散取值。而pip_ipi代表了X取值为i的概率,log为以2或者e为底的对数。举个例子,比如X有2个可能的取值,而这两个取值各为1/2时X的熵最大,此时X具有最大的不确定性。值为H(X)=−(12log12+12log12)=log2H(X) = -(\frac{1}{2}log\frac{1}{2} + \frac{1}{2}log\frac{1}{2}) = log2H(X)=−(21log21+21log21)=log2。如果一个值概率大于1/2,另一个值概率小于1/2,则不确定性减少,对应的熵也会减少。比如一个概率1/3,一个概率2/3,则对应熵为H(X)=−(13log13+23log23)=log3−23log2<log2)H(X) = -(\frac{1}{3}log\frac{1}{3} + \frac{2}{3}log\frac{2}{3}) = log3 - \frac{2}{3}log2 < log2)H(X)=−(31log31+32log32)=log3−32log2<log2)
熟悉了一个变量X的熵,很容易推广到多个个变量的联合熵,这里给出两个变量X和Y的联合熵表达式:
H(X,Y)=−∑i=1np(xi,yi)logp(xi,yi)H(X,Y) = -\sum\limits_{i=1}^{n}p(x_i,y_i)logp(x_i,y_i)H(X,Y)=−i=1∑np(xi,yi)logp(xi,yi)
有了联合熵,又可以得到条件熵的表达式H(X|Y),条件熵类似于条件概率,它度量了我们的X在知道Y以后剩下的不确定性。表达式如下:
H(X∣Y)=−∑i=1np(xi,yi)logp(xi∣yi)=∑j=1np(yj)H(X∣yj)H(X|Y) = -\sum\limits_{i=1}^{n}p(x_i,y_i)logp(x_i|y_i) = \sum\limits_{j=1}^{n}p(y_j)H(X|y_j)H(X∣Y)=−i=1∑np(xi,yi)logp(xi∣yi)=j=1∑np(yj)H(X∣yj)
好吧,绕了一大圈,终于可以重新回到ID3算法了。我们刚才提到H(X)度量了X的不确定性,条件熵H(X|Y)度量了我们在知道Y以后X剩下的不确定性,那么H(X)-H(X|Y)呢?从上面的描述大家可以看出,它度量了X在知道Y以后不确定性减少程度,这个度量我们在信息论中称为互信息,,记为I(X,Y)。在决策树ID3算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大,则越适合用来分类。
上面一堆概念,大家估计比较晕,用下面这个图很容易明白他们的关系。左边的椭圆代表H(X),右边的椭圆代表H(Y),中间重合的部分就是我们的互信息或者信息增益I(X,Y), 左边的椭圆去掉重合部分就是H(X|Y),右边的椭圆去掉重合部分就是H(Y|X)。两个椭圆的并就是H(X,Y)。

2. 决策树ID3算法的思路
上面提到ID3算法就是用信息增益大小来判断当前节点应该用什么特征来构建决策树,用计算出的信息增益最大的特征来建立决策树的当前节点。这里我们举一个信息增益计算的具体的例子。比如我们有15个样本D,输出为0或者1。其中有9个输出为0, 6个输出为1。 样本中有个特征A,取值为A1,A2和A3。在取值为A1的样本的输出中,有3个输出为1, 2个输出为0,取值为A2的样本输出中,2个输出为1,3个输出为0, 在取值为A3的样本中,4个输出为1,1个输出为0.
样本D的熵为:H(D)=−(915log2915+615log2615)=0.971H(D) = -(\frac{9}{15}log_2\frac{9}{15} + \frac{6}{15}log_2\frac{6}{15}) = 0.971H(D)=−(159log2159+156log2156)=0.971
样本D在特征下的条件熵为: H(D∣A)=515H(D1)+515H(D2)+515H(D3)H(D|A) = \frac{5}{15}H(D1) + \frac{5}{15}H(D2) + \frac{5}{15}H(D3)H(D∣A)=155H(D1)+155H(D2)+155H(D3)
=−515(35log235+25log225)−515(25log225+35log235)−515(45log245+15log215)=0.888= -\frac{5}{15}(\frac{3}{5}log_2\frac{3}{5} + \frac{2}{5}log_2\frac{2}{5}) - \frac{5}{15}(\frac{2}{5}log_2\frac{2}{5} + \frac{3}{5}log_2\frac{3}{5}) -\frac{5}{15}(\frac{4}{5}log_2\frac{4}{5} + \frac{1}{5}log_2\frac{1}{5}) = 0.888=−155(53log253+52log252)−155(52log252+53log253)−155(54log254+51log251)=0.888
对应的信息增益为I(D,A)=H(D)−H(D∣A)=0.083I(D,A) = H(D) - H(D|A) = 0.083I(D,A)=H(D)−H(D∣A)=0.083
下面我们看看具体算法过程大概是怎么样的。
输入的是m个样本,样本输出集合为D,每个样本有n个离散特征,特征集合即为A,输出为决策树T。
算法的过程为:
1)初始化信息增益的阈值ϵ
2)判断样本是否为同一类输出Di,如果是则返回单节点树T。标记类别为Di
3) 判断特征是否为空,如果是则返回单节点树T,标记类别为样本中输出类别D实例数最多的类别。
4)计算A中的各个特征(一共n个)对输出D的信息增益,选择信息增益最大的特征Ag
5) 如果Ag的信息增益小于阈值ϵ,则返回单节点树T,标记类别为样本中输出类别D实例数最多的类别。
6)否则,按特征Ag的不同取值Agi将对应的样本输出D分成不同的类别Di。每个类别产生一个子节点。对应特征值为Agi。返回增加了节点的数T。
7)对于所有的子节点,令D=Di,A=A−{Ag}递归调用2-6步,得到子树Ti并返回。
3. 决策树ID3算法的不足
ID3算法虽然提出了新思路,但是还是有很多值得改进的地方。
a)ID3没有考虑连续特征,比如长度,密度都是连续值,无法在ID3运用。这大大限制了ID3的用途。
b)ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现,在相同条件下,取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值,各为1/2,另一个变量为3个值,各为1/3,其实他们都是完全不确定的变量,但是取3个值的比取2个值的信息增益大。如果校正这个问题呢?
c) ID3算法对于缺失值的情况没有做考虑
d) 没有考虑过拟合的问题
相关文章:

决策树ID3算法
1. 决策树ID3算法的信息论基础 机器学习算法其实很古老,作为一个码农经常会不停的敲if, else if, else,其实就已经在用到决策树的思想了。只是你有没有想过,有这么多条件,用哪个条件特征先做if,哪个条件特征后做if比较优呢&#…...

C++模板基础(一)
函数模板(一) ● 使用 template 关键字引入模板: template void fun(T) {…} – 函数模板的声明与定义 – typename 关键字可以替换为 class ,含义相同 – 函数模板中包含了两对参数:函数形参 / 实参;模板形…...
)
生产者消费者模型线程池(纯代码)
目录 生产者消费者模型 条件变量&&互斥锁(阻塞队列) makefile Task.hpp BlockQueue.hpp BlockQueueTest.cc 信号量&&互斥锁(环形队列) makefile RingQueue.hpp RingQueueTest.cc 线程池(封…...

K8s 应用的网络可观测性: Cilium VS DeepFlow
随着分布式服务架构的流行,特别是微服务等设计理念在现代应用普及开来,应用中的服务变得越来越分散,因此服务之间的通信变得越来越依赖网络,很有必要来谈谈实现微服务可观测性中越来越重要的一环——云原生网络的可观测。K8s 是微服务设计理念能落地的最重要的承载体,本文…...
3.29面试题
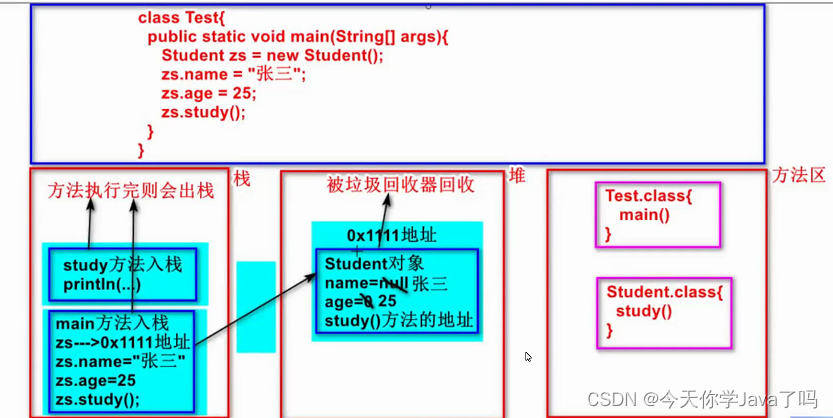
文章目录内存内存管理执行过程要点面试题内存 内存管理 由JVM管理 堆:new出来的对象(包括成员变量、数组元素、方法的地址)栈:局部变量(包括方法的参数)方法区:.class字节码文件(…...
操作系统漏洞发现
操作系统漏洞发现前言一、操作系统漏洞发现1.1 namp2. Goby3. Nessus二,进行渗透测试2.1 使用工具进行渗透1. metasploit2.2 EXP2.3 复现文章三,操作系统漏洞修复前言 不管是对于App来说,还是web站点来说,操作系统是必须的&#x…...
Linux gdb调试底层原理
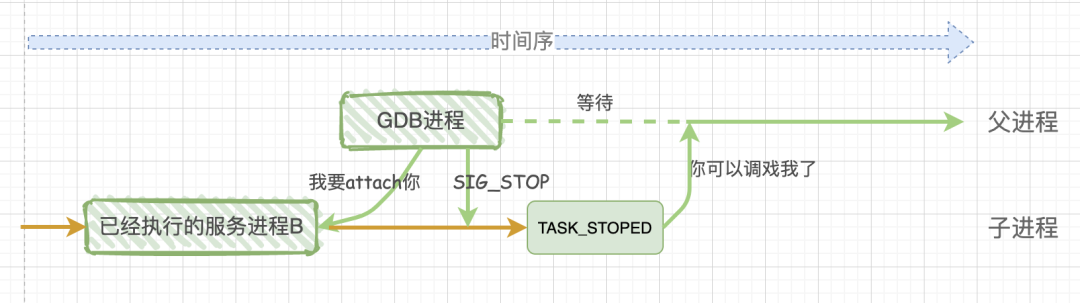
TOC 前言 linux下gdb调试程序操作过程参考本人文章:gdb调试操作; 这里不再叙述; 本文主要内容是介绍GDB本地调试的底层调试原理,我们来看一下GDB是通过什么机制来控制被调试程序的执行顺序; 总结部分是断点调试的底层原理,可以直接跳转过去先看看大概…...
)
LC-1647. 字符频次唯一的最小删除次数(哈希+计数)
1647. 字符频次唯一的最小删除次数 难度中等56 如果字符串 s 中 不存在 两个不同字符 频次 相同的情况,就称 s 是 优质字符串 。 给你一个字符串 s,返回使 s 成为 优质字符串 需要删除的 最小 字符数。 字符串中字符的 频次 是该字符在字符串中的出现…...

HTTP状态码
100: 接受,正在继续处理 200: 请求成功,并返回数据 201: 请求已创建 202: 请求已接受 203: 请求成为,但未授权 204: 请求成功,没有内容 205: 请求成功,重置内容 206: 请求成功,返回部分内容 301: 永久性重定…...

【Linux】初见“which命令”,“find命令”以及linux执行命令优先级
文章目录1.which命令1.1 whereis命令1.2 locate命令1.3 搜索文件命令总结2.find命令2.1 find之exec用法2.2 管道符之xargs用法3 Linux常用命令4.命令执行优先级1.which命令 查找命令文件存放目录 搜索范围由环境变量PATH决定(echo $PATH) which命令格式࿱…...

update case when 多字段,多条件, mysql中case when用法
文章目录 前言 sql示例 普通写法: update case when写法 update case when 多字段写法 case when语法 case when 的坑 1、不符合case when条件但是字段被更新为null了 解决方法一:添加where条件 解决方法二:添加else 原样输出 2、同一条数据符…...
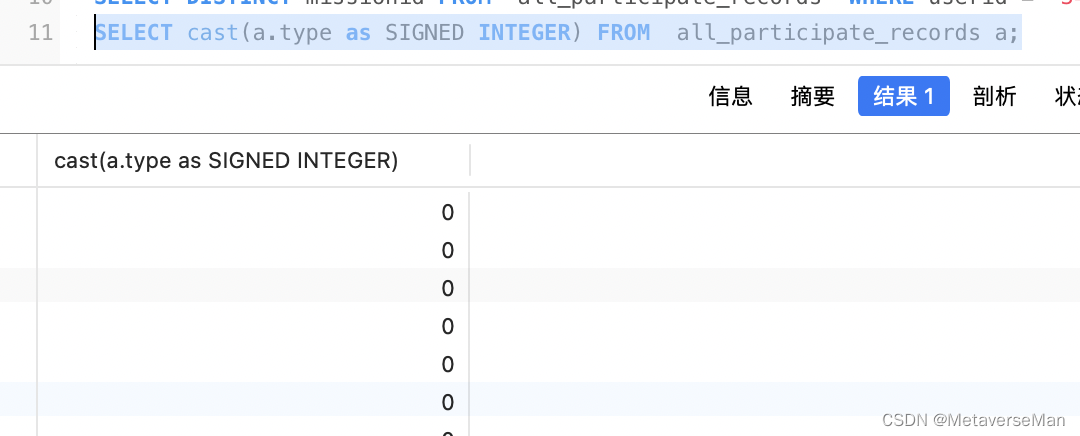
mysql隐式转换 “undefined“字符串匹配到mysql int类型0值字段
描述:mysql 用字符串搜索 能搜到int类型查询结果 mysql int类型条件用字符串查询 table: CREATE TABLE all_participate_records (id bigint unsigned NOT NULL AUTO_INCREMENT,created_at datetime(3) DEFAULT NULL,updated_at datetime(3) DEFAULT NULL,deleted…...

Redis八股文
1.Redis是什么? Redis 是一个基于 C 语言开发的开源数据库(BSD 许可),与传统数据库不同的是 Redis 的数据是存在内存中的(内存数据库),读写速度非常快,被广泛应用于缓存方向。并且,…...

InnoDB——详细解释锁的应用,一致性读,自增长与外键
一致性非锁定读 一致性的非锁定读(consistent nonlocking read)是指InnoDB存储引擎通过行多版本控制的方式读取当前执行时数据库中行的数据。 如果读取的行正在执行 行Delete或Update操作,这时读取操作不会因此去等待行上锁的释放。相反&…...

C++模板基础(四)
函数模板(四) ● 函数模板的实例化控制 – 显式实例化定义: template void fun(int) / template void fun(int) //header.h template<typename T> void fun(T x) {std::cout << x << std::endl; }//main.cpp #include&quo…...

pycharm使用记录
文章目录下载安装后续其他设置编辑器设置关于debug下载安装 直接去pycharm官网下载社区版,这个版本本来就是免费的,而且功能其实已经够了 后续其他设置 首先,第一次启动时,记得在preference->interpreter中设置python环境&a…...

Linux命令·kill·killall
Linux中的kill命令用来终止指定的进程(terminate a process)的运行,是Linux下进程管理的常用命令。通常,终止一个前台进程可以使用CtrlC键,但是,对于一个后台进程就须用kill命令来终止,我们就需…...

Linux /proc/version 文件解析
/proc/version文件里面的内容: Linux version 4.14.180-perf (oe-user@oe-host) (clang version 10.0.5 for Android NDK, GNU ld (GNU Binutils) 2.29.1.20180115) #1 SMP PREEMPT Wed Mar 29 18:55:02 CST 2023 /proc/version文件里面记录了如下内容: 1、Linux kernel的…...

【Django 网页Web开发】15. 实战项目:管理员增删改查,md5密码和密码重置(08)(保姆级图文)
目录1. model编写数据表2. 管理员列表2.1 admin.py视图文件2.2 admin_list.html2.3 url.py2.4 最终效果3. 管理员添加3.0 md5包的书写3.1 form.py表单组件3.2 admin.py视图文件3.3 引入公共的添加数据html3.4 url.py3.5 最终效果4. 管理员编辑4.0 form表单组件4.1 admin.py视图…...

STL容器之<array>
文章目录测试环境array介绍头文件模块类定义对象构造初始化元素访问容器大小迭代器其他函数测试环境 系统:ubuntu 22.04.2 LTS 64位 gcc版本:11.3.0 编辑器:vsCode 1.76.2 array介绍 array是固定大小的序列式容器,它包含按严格…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
