《深度学习》—— ResNet 残差神经网络
文章目录
- 一、什么是ResNet?
- 二、残差结构(Residual Structure)
- 三、Batch Normalization(BN----批归一化)
一、什么是ResNet?
-
ResNet 网络是在 2015年 由微软实验室中的何凯明等几位大神提出,斩获当年ImageNet竞赛中分类任务第一名,目标检测第一名。获得COCO数据集中目标检测第一名,图像分割第一名。
-
ResNet 网络中的两个核心组成部分
- 残差结构(Residual Structure)
- Batch Normalization(批归一化)
-
为什么要提出残差结构?
-
在ResNet 网络没有提出来之前,所有的神经网络都是通过卷积层和池化层的叠加组成的。
-
很多人认为卷积层和池化层的层数越多,模型的效果会越好
-
在实际的试验中发现,随着卷积层和池化层的叠加,学习效果不会逐渐变好,反而出现2个问题:
1.梯度消失和梯度爆炸
梯度消失:若每一层的误差梯度小于1,反向传播时,网络越深,梯度越趋近于0
梯度爆炸:若每一层的误差梯度大于1,反向传播时,网络越深,梯度越来越大2.退化问题
随着层数的增加,预测效果反而越来越差, 下面是何凯明他们论文中实验的可视化图,可以看出模型层数多的反而没有少的效果好
-
-
为了解决梯度消失或梯度爆炸问题,论文提出通过数据的预处理以及在网络中使用 BN(Batch Normalization)层来解决。
-
为了解决深层网络中的退化问题,可以人为地让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系。这种神经网络被称为 残差网络 (ResNets)
-
ResNet论文提出了 residual结构(残差结构)来减轻退化问题,下图是使用residual结构的卷积网络,可以看到随着网络的不断加深,效果并没有变差,而是变的更好了

-
ResNet 网络有不同数量的网络层模型,下图为 ResNet18、ResNet34、ResNet50、ResNet101、ResNet152 网络的表格化结构图:

二、残差结构(Residual Structure)
-
如下图所示,残差块包含两条路径,一条是主路径(通常包含多个卷积层),用于提取特征;另一条是恒等快捷连接,允许输入直接跳过主路径的某些层与输出相加
-
所谓相加是特征矩阵相同位置上的数字进行相加
-
两条路径的输出在特征维度上需要保持一致,以便进行相加操作。这通常通过调整卷积层的步长(stride)、使用1x1卷积核进行升维或降维等方式来实现。

-
以ResNet 18网络为例:
- 下面是 ResNet 18网络完整的图形化结构图

- 下面是 ResNet 18网络完整的图形化结构图
-
部分残差块如下:

-
非残差结构-第一层时(左边结构):
-
经过卷操作得到输出为[56,56,64]:
- 通过设置步长stride=1、3x3卷积和卷积核64,使得高宽与卷积核不变
- 激活函数relu处理
- 通过设置步长stride=1、3x3卷积和卷积核64,重复特征提取
-
残差结构-第二层(右边结构):
-
由上一层的输入为[56,56,64]——>输出为[28,28,128]:
- 通过设置步长stride=2、3x3卷积和卷积核128,使得高宽从56缩减一半到28,卷积核从64个更改为128个
- 激活函数relu处理
- 通过设置步长stride=1、3x3卷积和卷积核128,重复特征提取
-
快捷连接的输入为[56,56,64]——>[1x1x128]——>输出为[28,28,128]:
- 通过设置步长stride=2、1x1卷积和卷积核更改,使得高宽从56缩减一半到28,卷积核从64个更改为128个。
- 与经过卷积层处理后的输出值相加
三、Batch Normalization(BN----批归一化)
参考博客
-
所谓Feature Map(特征图)是卷积核卷出来的,你用各种情况下的卷积核去乘以原图,会得到各种各样的feature map。
-
在输入一张图片时往往会使用预处理来使得图片满足某一个分布规律,以加快特征提取。然后进行一次卷积得到一个feature map,而这个feature map就不一定还满足之前所要求的分布规律。
-
Batch Normalization是指批标准化处理,将一批数据的feature map满足均值为0,方差为1的分布规律。注意不是对某一张图片的feature map,而是一整批的feature map,因为BN需要计算整个batch的均值和方差。
-
如下图

-
原理
- 标准化处理:在训练过程中,对每个小批量数据进行标准化处理,即对每个特征维度进行归一化操作。这有助于缓解内部协变量偏移(Internal Covariate Shift)问题,即网络在训练过程中由于参数更新导致的数据分布变化问题。
- 可学习参数:为了恢复出原始网络所要学习的特征分布,BN引入了可学习的缩放因子(γ)和偏移因子(β),使得网络可以通过学习这些参数来调整标准化后的数据分布。
- 训练与测试:在训练阶段,BN使用当前小批量数据的均值和方差进行标准化处理;在测试阶段,则使用训练过程中所有小批量数据的均值和方差的移动平均进行标准化处理。
-
使用注意
-
(1)训练时要将traning参数设置为True进行统计,在验证时将trainning参数设置为False,对统计的值进行验证。在pytorch中可通过创建模型的model.train()和model.eval()方法控制。
-
(2)batch_size (每次迭代中,模型同时处理多少个数据点)尽可能设置大点,设置小后表现可能很糟糕,设置的越大求的均值和方差越接近整个训练集的均值和方差。
-
(3)建议将BN层放在卷积层(Conv)和激活层(例如Relu)之间
-
相关文章:

《深度学习》—— ResNet 残差神经网络
文章目录 一、什么是ResNet?二、残差结构(Residual Structure)三、Batch Normalization(BN----批归一化) 一、什么是ResNet? ResNet 网络是在 2015年 由微软实验室中的何凯明等几位大神提出,斩获…...

针对考研的C语言学习(定制化快速掌握重点3)
1.数组常见错误 数组传参实际传递的是数组的起始地址,若在函数中改变数组内容,数组本身也会发生变化 #include<stdio.h> void change_ch(char* str) {str[0] H; } int main() {char ch[] "hello";change_ch(ch);printf("%s\n&q…...

pikachu XXE(XML外部实体注入)通关
靶场:pikachu 环境: 系统:Windows10 服务器:PHPstudy2018 靶场:pikachu 关卡提示说:这是一个接收xml数据的api 常用的Payload 回显 <?xml version"1.0"?> <!DOCTYPE foo [ <!ENTITY …...

shell脚本定时任务通知到钉钉
shell脚本定时任务通知到钉钉 1、背景 前两天看了一下定时任务,垃圾清理、日志相关、系统巡检这些,有的服务器运行就有问题,或者不运行,正好最近在做运维标准重制运维手册,顺便把自动化这块优化一下,所…...
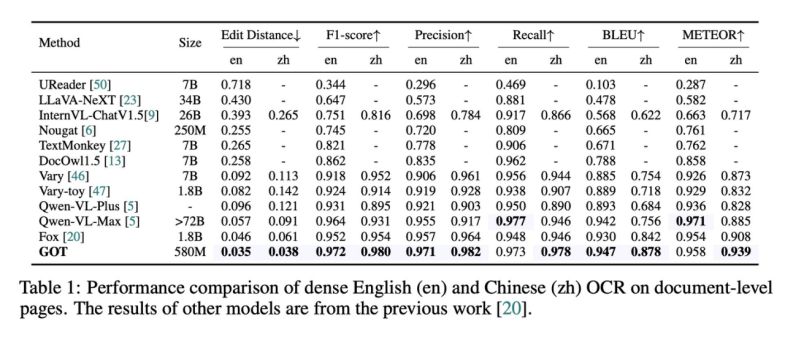
2.4K star的GOT-OCR2.0:端到端OCR 模型
GOT-OCR2.0是一款新一代的光学字符识别(OCR)技术,标志着人工智能在文本识别领域的重大进步。作为一款开源模型,GOT-OCR2.0不仅支持传统的文本和文档识别,还能够处理乐谱、图表以及复杂的数学公式,为用户提供…...

【JavaEE】——线程的安全问题和解决方式
阿华代码,不是逆风,就是我疯,你们的点赞收藏是我前进最大的动力!!希望本文内容能够帮助到你! 目录 一:问题引入 二:问题深入 1:举例说明 2:图解双线程计算…...

初步认识了解分布式系统
背景认识:我们要学习redis,还是得了解一下什么是分布式。为什么呢?因为redis只有在分布式系统中才能发挥它最大的作用,也就是领域展开,所以接下来我们就简单过一下什么是分布式系统 一些术语认识: &#x…...

react 为什么不能学习 vue3 进行静态节点标记优化性能?
因为 React 使用的是 JSX,而 JSX 本质上就是 JS 语言,是具有非常高的动态的,而 Vue 使用的 template 则是给了足够的约束,比如说 Vue 的 template 里面使用了很多特定的标记来做不同的事情,比如说 v-if 就是进行变量判…...

Elasticsearch黑窗口启动乱码问题解决方案
问题描述 elasticsearch启动后有乱码现象 解决方案: 提示:这里填写该问题的具体解决方案: 到 \config 文件下找到 jvm.options 文件 打开后 在文件末尾空白处 添加 -Dfile.encodingGBK 保存后重启即可。...

Logtus IT员工参加国际技术大会
Logtus IT的员工参加了国际技术大会,该大会致力于在金砖国家框架内开发俄罗斯的技术。该活动包括一个展览,俄罗斯开发商展示了他们的信息技术、电子和电信成就。展示了面向国内和国际市场(包括政府机构)的解决方案、产品和平台。 …...

ant design vue组件中table组件设置分组头部和固定总结栏
问题:遇到了个需求,不仅要设置分组的头部,还要在顶部有个统计总和的栏。 分组表头的配置主要是这个,就是套娃原理,不需要展示数据的直接写个title就行,需要展示数据的字段才需要详细的配置属性。 const co…...
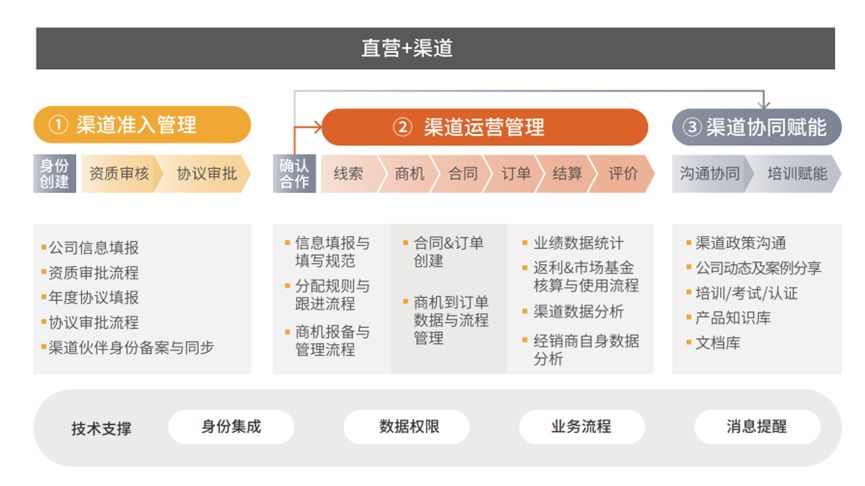
2024年信息安全企业CRM选型与应用研究报告
数字化的生活给人们带来便利的同时也带来一定的信息安全隐患,如网络侵权、泄露用户隐私、黑客攻击等。在互联网高度发展的今天,信息安全与我们每个人、每个组织甚至每个国家都息息相关。 信息安全行业蓬勃发展。根据智研咨询数据,2021年&…...

【后端开发】JavaEE初阶——计算机是如何工作的???
前言: 🌟🌟本期讲解计算机工作原理,希望能帮到屏幕前的你。 🌈上期博客在这里:【MySQL】MySQL中JDBC编程——MySQL驱动包安装——(超详解) 🌈感兴趣的小伙伴看一看小编主…...
源码安装postgresql16.3)
Linux(Ubuntu)源码安装postgresql16.3
文章目录 Linux(Ubuntu)源码安装postgresql016.3下载程序包编译安装软件初次执行configure错误调试1:configure: error: ICU library not found再次执行configureBuild 设置环境初始化数据库启动数据库参考 Linux(Ubuntu)源码安装…...
面向对象 | 7.6、多态)
Python 入门教程(7)面向对象 | 7.6、多态
文章目录 一、多态1、鸭子类型2、实现多态的机制2.1、鸭子类型2.2、继承与重写 3、Python多态的优势4、总结 前言: 在面向对象编程(OOP)中,多态(Polymorphism)是一种非常重要的概念,多态就是同一…...

Cilium + ebpf 系列文章-什么是ebpf?(一)
前言: 这篇非常非常干,很有可能读不懂。 这里非常非常推荐,建议使用Cilium官网的lab来辅助学习!!!Resources Library - IsovalentExplore Isovalents Resource Library, your one-stop destination for ins…...

RabbitMQ08_保证消息可靠性
保证消息可靠性 一、生产者可靠性1、生产者重连机制(防止网络波动)2、生产者确认机制Publisher Return 确认机制Publisher Confirm 确认机制 二、MQ 可靠性1、数据持久化交换机、队列持久化消息持久化 2、Lazy Queue 惰性队列 三、消费者可靠性1、消费者…...

恶意Bot流量识别分析实践
1、摘要 随着互联网的发展,自动化工具和脚本(Bots)的使用越来越普遍。虽然一些善意 Bots 对于网站的正常运行和数据采集至关重要,但恶意 Bots 可能会对网站带来负面影响,如爬取敏感信息、恶意注册、刷流量等。因此&am…...
习题2 第四题)
Java2 实用教程(第6版)习题2 第四题
【源文件的命名与书中的不同】 四、阅读程序题 1、上机运行下列程序,注意观察输出的结果。 public class E2_1 {public static void main(String args[]){for(int i20302;i<20322;i){System.out.println((char) i);}} } 运行结果: 低 住 佐 佑 佒…...

HashMap和ConcurrentHashMap的区别
1.是什么 HashMap和ConcurrentHashMap都是Java集合框架中的成员,它们用于存储键值对,但它们在并发场景下的表现和行为有很大的不同。以下是它们之间的一些主要区别: 1. 并发安全性 HashMap: HashMap不是线程安全的。如果多个线程同时访问Has…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
