无限大薄板的电场

单块无限大薄板两端的电场

单块无限大的薄板，如果上面带有均匀分布的电荷，就会在薄板的两侧产生电场，电场大小与距离平板的位置无关，方向与平板垂直，如果平板带正电荷，则电场方向向外指向两侧，如果平板带负电荷，两侧的电场方向向内指向平板

公式

$$E=\frac{\sigma }{2{ϵ}_0}$$

其中：

• $E$ 是电场的大小
• $\sigma$ 是电荷密度
• ${ϵ}_0$ 是真空介电常数， $\frac{1}{4\pi {ϵ}_0}=9\ast 10^9$

解释

1.对称性

图示

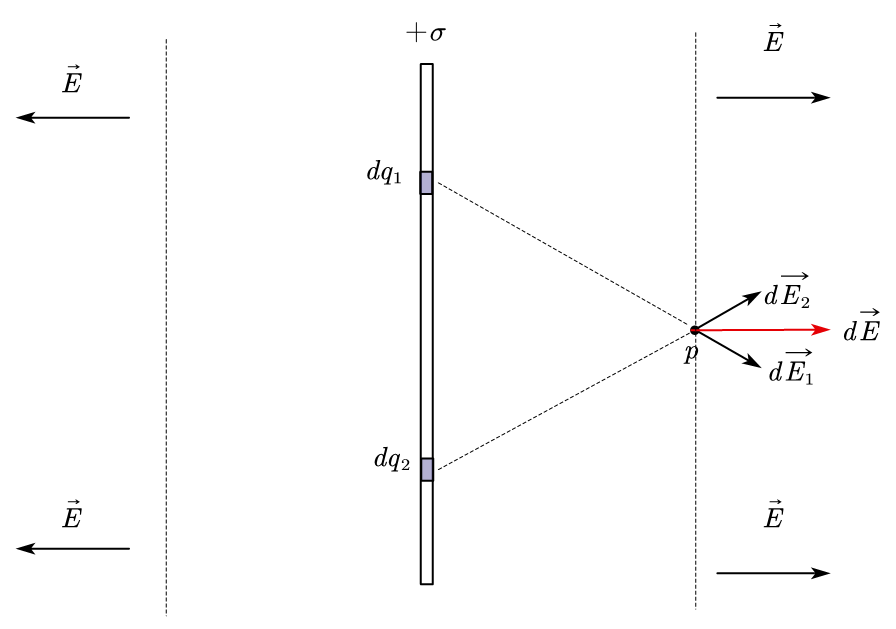
因为平板上的电荷是均匀分布的，所以在 p 点处的电场通过两个对称的电荷 $d{q}_1$，$d{q}_2$ 叠加后的电场方向为水平方向，与平板垂直，又因为平板无限大，所以每个位置都可以找到对称的两个部分产生水平的叠加电场，同时因为是均匀分布的电荷，所以在电场两侧产生的电场是一样大的。

2.利用高斯定律计算

图示

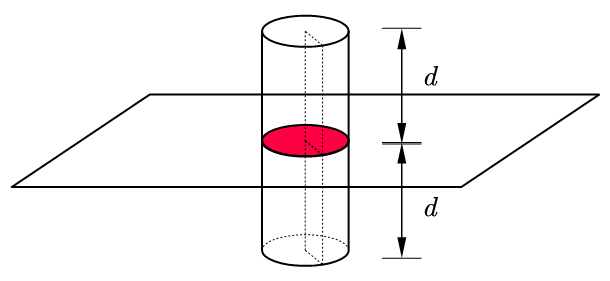
利用高斯定律，如下图所示，选取圆柱形的封闭曲面，曲面的上下两个面与平板的距离相等，中心部分的电荷量为

$$Q=\sigma A$$

其中

• $Q$ 是图中红色部分的电荷量
• $\sigma$ 是平板上的电荷密度
• $A$ 是图中红色部分的面积

根据高斯定律，穿过这个封闭曲面的电通量等于封闭曲面中的总的电荷量除以真空介电常数。

$$EA+EA+0=\frac{\sigma A}{{ϵ}_0}$$

其中两个 EA 是上下两个平面的电通量，0 是圆柱的曲面上没有电场通过，等号右侧是高斯定律的结论。

整理得

$$E=\frac{\sigma }{2{ϵ}_0}$$

两个无限大薄板的电场

如下图，两个均匀分布的无线大薄板产生的电场，一个带正电荷，另一个带相同电荷密度的负电荷。

图示

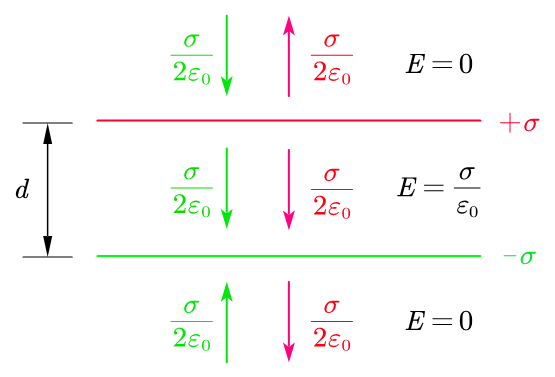
公式

$$E=\frac{\sigma }{{ϵ}_0}$$

其中

• $E$ 是电场的大小
• $\sigma$ 是电荷密度
• ${ϵ}_0$ 是真空介电常数， $\frac{1}{4\pi {ϵ}_0}=9\ast 10^9$

解释

由于无限大的薄板电场与距离无关，所以带正电荷的薄板产生的电场如图中的红色标识所示，带负电荷的薄板产生的电场如图中的绿色标识所示，经过电场叠加，两个薄板之外的电场大小相等，方向相反，相互抵消，两个薄板之间的电场相互叠加，方向相同，大小相等，所以变为单板的 2 倍，因此得到最终的电场为

$$E=\frac{\sigma }{{ϵ}_0}$$

参考

【麻省理工公开课：电和磁】 https://www.bilibili.com/video/BV1rW41147od/?p=3

【[中英字幕]2018年麻省理工MITx 8.02.1x 电学和磁学-静电学 Electricity and Magnetism-Electrostatics】 https://www.bilibili.com/video/BV16m4y1w7P8/?p=45