普通二叉搜索树的模拟实现【C++】
二叉搜素树简单介绍
二叉搜索树又称二叉排序树,是具有以下性质的二叉树:
-
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
-
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
-
它的左右子树也分别为二叉搜索树
注意:空树也是二叉搜索树
二叉搜素树的模型
- K模型:
K模型即只有key作为关键字,节点中只需要存储Key即可,关键字即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- KV模型:
每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
该种方式在现实生活中非常常见:
比如
英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出
现次数就是<word, count>就构成一种键值对。
K模式和KV模式实现上基本一样,就是节点中存储的是key还是<key,val>的区别
二叉搜素树的性能
二叉搜索树的性能取决于树的高度,因为一次查找最多查找高度次,而删除和插入也是在查找的基础上增加了一些O(1)的操作
在最理想的情况下,树是完全平衡的,平均查找、插入和删除的时间复杂度O(log N)。
但在最坏的情况下,树可能退化成一个链表,此时这些操作的时间复杂度将增加到O(N)。
例:

全部的实现代码放在了文章末尾
准备工作
创建两个文件,一个头文件BSTree.hpp,一个源文件test.cpp
【因为模板的声明和定义不能分处于不同的文件中,所以把成员函数的声明和定义放在了同一个文件BSTree.hpp中】
-
RBTree.hpp:存放包含的头文件,命名空间的定义,成员函数和命名空间中的函数的定义
-
test.cpp:存放main函数,以及测试代码
包含头文件
iostream:用于输入输出
类的成员变量

构造函数和拷贝构造
构造函数没什么好说的,默认构造就行了
BSTree() :_root(nullptr)
{}拷贝构造:
因为节点都是从堆区new出来的,所以要深拷贝
使用递归实现深拷贝:
因为拷贝构造不能有多余的参数,但是递归函数又必须使用参数记录信息
所以再封装一个成员函数,专门用来递归拷贝:

然后在拷贝构造里面调用一下这个函数就行了
拷贝构造
BSTree(const BSTree& obj)
{_root = Copy(obj._root);
}
swap和赋值运算符重载
交换两颗二叉搜索树的本质就是交换两颗数的资源(数据),而它们的资源都是从堆区申请来的,然后用指针指向这些资源

并不是把资源存储在了二叉搜索树对象中
所以资源交换很简单,直接交换_root指针的指向即可
void Swap(BSTree& obj)
{std::swap(_root, obj._root);
}
赋值运算符重载
BSTree& operator=(BSTree obj)
{this->Swap(obj);return *this;
}
为什么上面的两句代码就可以完成深拷贝呢?
这是因为:
使用了传值传参,会在传参之前调用拷贝构造,再把拷贝构造出的临时对象作为参数传递进去
赋值运算符的左操作数,*this再与传入的临时对象obj交换,就直接完成了拷贝
在函数结束之后,存储在栈区的obj再函数结束之后,obj生命周期结束
obj调用析构函数,把指向的从*this那里交换来的不需要的空间销毁
析构函数
使用递归遍历,把所有从堆区申请的节点都释放掉:
因为析构函数不能有多余的参数,但是递归函数又必须使用参数记录信息
所以再封装一个成员函数,专门用来递归释放:

然后在拷贝构造里面调用一下这个函数就行了
析构函数
~BSTree()
{Destroy(_root);_root = nullptr;
}
find
具体流程:
从根节点开始,将目标值(传入的key)与当前节点的key进行比较。
如果目标值小于当前节点值,则在左子树中继续查找;
如果目标值大于当前节点值,则在右子树中继续查找。
这个过程一直进行,直到找到与目标值或者到达空节点为止。
把上述过程转成代码:

insert
插入的具体过程如下:
-
树为空,则直接新增节点,赋值给二叉搜索树的成员变量
_root指针 -
树不空,则按照查找(
find)的逻辑找到新节点应该插入的位置 -
树不空,如果树中已经有了一个节点的key值与要插入的节点的key相同,就插入失败
这个过程一直进行,直到找到与传入的key相等的节点或者到达空节点为止。
把上述过程转成代码:

erase
删除操作较为复杂,需要先在数中找到要删除的节点,再根据要删除节点的子节点数量进行不同的处理:
-
如果要删除节点没有子节点,则直接删除该节点。
-
如果要删除节点有一个子节点(子树),则用其子节点(子树)替换该节点。
-
如果要删除节点有两个子节点(子树)
在右子树中找到最小值的节点(或左子树中找到最大值的节点)来替换待删除节点,然后删除那个最小值(或最大值)的节点
情况1可以和情况2合并一下
把上述过程转成代码:
bool Erase(const K& key)
{Node* cur = _root;从根节点开始Node* parent = nullptr;先找到要删除的节点(cur)while (cur)如果到了空节点就结束循环{if (cur->_key < key) 目标值`大于`当前节点值,则在`右子树`中继续查找{parent = cur;cur = cur->_right;}else if (cur->_key > key) 目标值'小于'当前节点值,则在'左子树'中继续查找{parent = cur;cur = cur->_left;}else{break;找到要删除的节点了,结束循环}}如果找到空节点了,还没找到要删除的节点就说明树里面本来就没有这个key,不需要删除if (cur == nullptr){return false; 删除失败,返回false}else{如果 左 子树为空, 右 子树不为空(或者左右都为空)即只有右子节点(右子树)或者没有子节点if (cur->_left == nullptr){如果父亲节点为空,就表示cur为根节点if (parent == nullptr){使用右子节点,代替根节点_root = cur->_right;}else 根据cur与它的父亲节点的链接关系{if (cur == parent->_left){使用右子节点,代替curparent->_left = cur->_right;}else{使用右子节点,代替curparent->_right = cur->_right;}}delete cur; 删除cur节点,即要删除的节点}如果 右 子树为空, 左 子树不为空(或者左右都为空)即只有左子节点(左子树)或者没有子节点else if (cur->_right == nullptr){如果父亲节点为空,就表示cur为根节点if (parent == nullptr){使用左子节点,代替根节点_root = cur->_left;}else 根据cur与它的父亲节点的链接关系{if (cur == parent->_left){使用左子节点,代替curparent->_left = cur->_left;}else{使用左子节点,代替curparent->_right = cur->_left;}}delete cur; 删除cur节点,即要删除的节点}else 如果左右子树都不为nullptr{去cur(要删除的节点)的右子树中找key最小的节点Node* tmp = cur->_right;Node* prev = cur;二叉搜索树的最小节点,一定在这颗树的最左边while (tmp->_left) 所以一直往左走,直到左子树为nullptr{prev = tmp;tmp = tmp->_left; 往左走}用右子树中key最小的节点的数据,替换cur中的数据也就相当于把cur(要删除的节点)删除了cur->_key = tmp->_key;cur->_val = tmp->_val;如果prev == cur,就说明tmp就是key最小的节点了此时tmp在cur(prev)的右边if (prev == cur){把cur(prev)的 右边 连上tmp的右子树因为tmp虽然是最左节点,但是它有可能还有右孩子cur->_right = tmp->_right;delete tmp;}else{把prev的 左边 连上tmp的右子树因为tmp虽然是最左节点,但是它有可能还有右孩子prev->_left = tmp->_right;delete tmp;}}}return true; 删除成功,返回true
}
empty
bool Empty()
{如果_root为空,那么树就是空的return _root == nullptr;
}
size
使用递归实现二叉搜索树的节点个数统计:
因为我们经常使用的stl的容器的size都是没有参数的,但是递归函数又必须使用参数记录信息
所以再封装一个成员函数,专门用来递归:

然后再size里面调用一下就行了
size_t Size()
{return _Size(_root);
}
中序遍历
中序遍历的递归函数:

然后再调用递归函数
void InOrder()
{_InOrder(_root);
}
全部代码
#include<iostream>
using namespace std;template<class K, class V>
struct BSTreeNode
{K _key;V _val;BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;BSTreeNode(const K& key, const V& val):_left(nullptr), _right(nullptr){_key = key;_val = val;}
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:BSTree() :_root(nullptr){}BSTree(const BSTree& obj){_root = Copy(obj._root);}BSTree& operator=(BSTree obj){this->Swap(obj);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}void Swap(BSTree& obj){std::swap(_root, obj._root);}bool Insert(const K& key, const V& val){if (_root == nullptr)//树为空,则直接新增节点{//赋值给二叉搜索树的成员变量`_root`指针_root = new Node(key, val);return true;//返回true,代表插入成功}Node* cur = _root;//从根节点开始//定义parent来保存cur的父亲节点//假设根节点的父亲节点为nullptrNode* parent = nullptr;while (cur){if (cur->_key < key)//目标值`大于`当前节点值,则在`右子树`中继续查找{parent = cur;cur = cur->_right;}else if (cur->_key > key)//目标值'小于'当前节点值,则在'左子树'中继续查找{parent = cur;cur = cur->_left;}else{return false;}}Node* newnode = new Node(key, val);if (parent->_key > key){parent->_left = newnode;}else{parent->_right = newnode;}return true;}Node* Find(const K& key){Node* cur = _root;//从根节点开始while (cur)//如果到了空节点就结束循环{if (cur->_key < key)//目标值`大于`当前节点值,则在`右子树`中继续查找{cur = cur->_right;}else if (cur->_key > key)//目标值'小于'当前节点值,则在'左子树'中继续查找{cur = cur->_left;}else//如果相等,就找到了{return cur;}}return nullptr;//找不到就返回nullptr}bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{break;}}if (cur == nullptr)return false;else{if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (cur == parent->_left)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else{Node* tmp = cur->_right;Node* prev = cur;while (tmp->_left){prev = tmp;tmp = tmp->_left;}cur->_key = tmp->_key;cur->_val = tmp->_val;if (prev == cur){cur->_right = tmp->_right;delete tmp;}else{prev->_left = tmp->_right;delete tmp;}}}return true;}void InOrder(){_InOrder(_root);}bool Empty(){return _root == nullptr;}size_t Size(){return _Size(_root);}size_t Height(){return _Height(_root);}
private:Node* _root = nullptr;size_t _Height(Node* root){if (root == nullptr)return 0;int left = _Height(root->_left);int right = _Height(root->_right);return left > right ? left + 1 : right + 1;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newnode = new Node(root->_key, root->_val);newnode->_left = Copy(root->_left);newnode->_right = Copy(root->_right);return newnode;}//使用 后序遍历 释放void Destroy(Node* root){//空节点不需要释放,直接返回if (root == nullptr)return;Destroy(root->_left);//递归释放左子树Destroy(root->_right);//递归释放右子树delete root;//释放根节点}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);//遍历左子树//打印信息cout << root->_key << ":" << root->_val << endl;_InOrder(root->_right);//遍历右子树}//直接遍历二叉树进行节点统计size_t _Size(Node* root){if (root == nullptr)return 0;//统计左子树节点个数int left = _Size(root->_left);//统计右子树节点个数int right = _Size(root->_right);return left + right + 1;//1是当前节点}
};相关文章:

普通二叉搜索树的模拟实现【C++】
二叉搜素树简单介绍 二叉搜索树又称二叉排序树,是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值 它的左右子树也分别为二叉搜索树 注意…...

unity 介绍Visual Scripting Scene Variables
Visual Scripting中的场景变量是指在Unity中使用可视化脚本时,能够在不同场景间传递和存储数据的变量。这些变量可以用来跟踪游戏状态、玩家信息或其他动态数据,允许开发者在不编写代码的情况下创建复杂的游戏逻辑。 场景变量的优势包括: 1…...

linux服务器部署filebeat
# 下载filebeat curl -L -O https://artifacts.elastic.co/downloads/beats/filebeat/filebeat-7.17.23-linux-x86_64.tar.gz # 解压 tar xzvf filebeat-7.17.23-linux-x86_64.tar.gz# 所在位置(自定义) /opt/filebeat-7.17.23-linux-x86_64/filebeat.ym…...

个人获取Wiley 、ScienceDirect、SpringerLink三个数据库文献的方法
在同学们的求助文献中经常出现Wiley 、ScienceDirect、SpringerLink这三个数据库文献。本文下面就讲解一下个人如何不用求助他人自己搞定这三个数据库文献下载的方法。 个人下载文献首先要先获取数据库资源,小编平时下载文献是通过科研工具——文献党下载器获取的数…...

Java五子棋
目录 一:案例要求: 二:代码: 三:结果: 一:案例要求: 实现一个控制台下五子棋的程序。用一个二维数组模拟一个15*15路的五子棋棋盘,把每个元素赋值位“┼”可以画出棋…...

【从0开始自动驾驶】用python做一个简单的自动驾驶仿真可视化界面
【从0开始自动驾驶】用python做一个简单的自动驾驶仿真可视化界面 废话几句废话不多说,直接上源码目录结构init.pysimulator.pysimple_simulator_app.pyvehicle_config.json 废话几句 自动驾驶开发离不开仿真软件成品仿真软件种类多https://zhuanlan.zhihu.com/p/3…...

一拖二快充线:单接与双接的多场景应用
在当代社会,随着智能手机等电子设备的普及,充电问题成为了人们关注的焦点。一拖二快充线作为一种创新的充电解决方案,因其便捷性与高效性而受到广泛关注。本文将深入探讨一拖二快充线的定义、原理以及在单接与双接手机场景下的应用࿰…...

接口自动化测试概述
目录 1 接口自动化测试简介 1.1 什么是接口 1.2 什么是接口测试 1.3 为什么要做接口测试 1.4 什么是接口测试自动化 1.5 为什么要做接口测试自动化 2 接口自动化测试规范 2.1 文档准备 2.1.1 需求文档 2.1.2 接口文档 2.1.3 UI 交互图 2.1.4 数据表设计文档 2.2 明…...

Fingerprint.js:精准用户识别的浏览器指纹技术
在数字化时代,用户识别成为互联网服务中不可或缺的一环。随着隐私保护意识的增强,传统的用户识别方法如Cookies和本地存储面临着越来越多的挑战。而Fingerprint.js作为一种创新的浏览器指纹技术,以其高效、隐私友好的特性,逐渐在个…...
Gson将对象转换为JSON(学习笔记)
JSON有两种表示结构,对象和数组。对象结构以"{"大括号开始,以"}"大括号结束。中间部分由0或多个以”,"分隔的”key(关键字)/value(值)"对构成,关键字和值之间以":"分隔,语法结…...

什么是IPv6
目前国内的网络正在快速的向IPv6升级中,从网络基础设施如运营商骨干网、城域网,到互联网服务商如各类云服务,以及各类终端设备厂商如手机、电脑、路由器、交换机等。目前运营商提供的IPv6线路主要分为支持前缀授权和不支持前缀授权两种。 说…...
python画图|放大和缩小图像
在较多的画图场景中,需要对图像进行局部放大,掌握相关方法非常有用,因此我们很有必要一起学习 【1】官网教程 首先是进入官网教程,找到学习资料: https://matplotlib.org/stable/gallery/subplots_axes_and_figures…...
Mac优化清理工具CleanMyMac X 4.15.6 for mac中文版
CleanMyMac X 4.15.6 for mac中文版下载是一款功能更加强大的系统优化清理工具,软件只需两个简单步骤就可以把系统里那些乱七八糟的无用文件统统清理掉,节省宝贵的磁盘空间。CleanMyMac X 4.15.6 for mac 软件与最新macOS系统更加兼容,流畅地…...

资质申请中常见的错误有哪些?
在申请建筑资质的过程中,企业可能会犯一些常见的错误,以下是一些需要避免的错误: 1. 资料准备不充分: 申请资质需要提交大量的资料,包括企业法人资料、财务报表、业绩证明等。资料不齐全或不准确都可能导致申请失败。…...

基于单片机的多路温度检测系统
**单片机设计介绍,基于单片机CAN总线的多路温度检测系统设计 文章目录 前言概要功能设计设计思路 软件设计效果图 程序设计程序 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师,一名热衷于单片机技术探…...

面试题:通过栈实现队列
题目描述: 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素i…...

网络战时代的端点安全演变
在恶意网络行为者与对手在世界各地展开网络战争的日常战争中,端点安全(中世纪诗人可能会称其为“守卫大门的警惕哨兵”)当然是我们的互联数字世界的大门。 端点安全类似于我们今天称之为现代企业的数字有机体的免疫系统,可以将…...
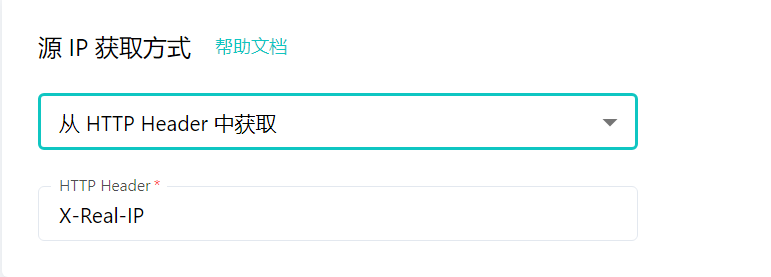
雷池 WAF 如何配置才能正确获取到源 IP
经常有大哥反馈说雷池攻击日志里显示的 IP 有问题。 这里我来讲一下为什么一些情况下雷池显示的攻击 IP 会有问题。 问题说明 默认情况下,雷池会通过 HTTP 连接的 Socket 套接字读取客户端 IP。在雷池作为最外层网管设备的时候这没有问题,雷池获取到的…...

libcrypto.so.10内容丢失导致sshd无法运行
说明: 我的是centos的服务器,被扫出有ssh漏洞,需要升级到OpenSSH_9.8p1, OpenSSL 3.0.14 4 报错 我的系统和环境升级前的版本 这是升级之后的版本 OpenSSH_9.8p1, OpenSSL 3.0.14 4 解决:我这个的原因是升级的时候把这个文件给删除了, 复制旧服务器上的 libcrypto.so.1…...

DTH11温湿度传感器
DHT11 是一款温湿度复合传感器,常用于单片机系统中进行环境温湿度的测量。以下是对 DHT11 温湿度传感器的详细讲解: 一、传感器概述 DHT11 数字温湿度传感器是一款含有已校准数字信号输出的温湿度复合传感器。它应用专用的数字模块采集技术和温湿度传感…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
