【机器学习(十)】时间序列案例之月销量预测分析—Holt-Winters算法—Sentosa_DSML社区版
文章目录
- 一、Holt-Winters算法原理
- (一) 加法模型
- (二) 乘法模型
- (三) 阻尼趋势
- 二、Holt Winters算法优缺点
- 优点
- 缺点
- 三、Python代码和Sentosa_DSML社区版算法实现对比
- (一) 数据读入和统计分析
- (二) 数据预处理
- (三) 模型训练和模型评估
- (四) 模型可视化
- 四、总结
一、Holt-Winters算法原理
什么是Holt-Winters预测算法?
Holt-Winters算法是一种时间序列预测方法。时间序列预测方法用于提取和分析数据和统计数据并表征结果,以便根据历史数据更准确地预测未来。Holt-Winters 预测算法允许用户平滑时间序列并使用该数据预测感兴趣的领域。指数平滑法会根据历史数据分配指数递减的权重和值,以降低较旧数据的权重值。换句话说,在预测中,较新的历史数据比较旧的结果具有更大的权重。
Holt-Winters中使用的指数平滑方法有三种:
单指数平滑——适用于预测没有趋势或季节性模式的数据,其中数据水平可能随时间而变化。
双重指数平滑法——用于预测存在趋势的数据。
三重指数平滑法——用于预测具有趋势和/或季节性的数据。
Holt-Winters包括预测方程和三个平滑方程,分别用于处理水平 ℓ t , \ell_{t}, ℓt, 趋势 b t b_{t} bt 和季节性成分 s t s t st ,对应的平滑参数分别是 α , β ∗ \alpha, \ \beta^{*} α, β∗ 和 γ \gamma γ 。通常用 m m m 表示季节性的周期,比如季度数据 m = 4 m=4 m=4 ,月度数据 m = 12 m=1 2 m=12 ,
Holt-Winters方法有两种变体,主要区别在于季节性成分的处理方式:
1. 加法模型:当季节性变化较为稳定时使用加法模型。
2. .乘法模型:当季节性变化与数据水平成比例变化时,适用乘法模型。
(一) 加法模型
在加法模型中,季节性成分用绝对值来表示,并在水平方程中通过减去季节性成分来对数据进行季节性调整。每年内,季节性成分的和大约为零。加法模型的分量形式为:
y ^ t + h ∣ t = ℓ t + h b t + s t + h − m ( k + 1 ) \hat{y}_{t+h | t}=\ell_{t}+h b_{t}+s_{t+h-m ( k+1 )} y^t+h∣t=ℓt+hbt+st+h−m(k+1)
包含三个平滑方程,其中,水平方程是一个加权平均,包含季节性调整后的观察值 ( y t − s t − m ) ( y_{t}-s_{t-m} ) (yt−st−m) 和非季节性预测值 ( ℓ t − 1 + b t − 1 ) ( \ell_{t-1}+b_{t-1} ) (ℓt−1+bt−1)
ℓ t = α ( y t − s t − m ) + ( 1 − α ) ( ℓ t − 1 + b t − 1 ) \ell_{t}=\alpha( y_{t}-s_{t-m} )+( 1-\alpha) ( \ell_{t-1}+b_{t-1} ) ℓt=α(yt−st−m)+(1−α)(ℓt−1+bt−1)
趋势方程与Holt的线性方法相同。
b t = β ∗ ( ℓ t − ℓ t − 1 ) + ( 1 − β ∗ ) b t − 1 b_{t}=\beta^{*} ( \ell_{t}-\ell_{t-1} )+( 1-\beta^{*} ) b_{t-1} bt=β∗(ℓt−ℓt−1)+(1−β∗)bt−1
季节性方程通过当前的季节性指数 ( y t − ℓ t − 1 − b t − 1 ) ( y_{t}-\ell_{t-1}-b_{t-1} ) (yt−ℓt−1−bt−1) 和上一年同一季节的季节性指数 s t − m s_{t-m} st−m 来平滑季节性成分。
s t = γ ( y t − ℓ t − 1 − b t − 1 ) + ( 1 − γ ) s t − m s_{t}=\gamma( y_{t}-\ell_{t-1}-b_{t-1} )+( 1-\gamma) s_{t-m} st=γ(yt−ℓt−1−bt−1)+(1−γ)st−m
(二) 乘法模型
在乘法模型中,季节性成分以相对值(百分比)表示,并通过将时间序列除以季节性成分来进行季节性调整。每年内,季节性成分的和约为 m ∘ m_{\circ} m∘ ,乘法模型的分量形式为:
y ^ t + h ∣ t = ( ℓ t + h b t ) s t + h − m ( k + 1 ) \hat{y}_{t+h | t}=( \ell_{t}+h b_{t} ) s_{t+h-m ( k+1 )} y^t+h∣t=(ℓt+hbt)st+h−m(k+1)
ℓ t = α y t s t − m + ( 1 − α ) ( ℓ t − 1 + b t − 1 ) \ell_{t}=\alpha{\frac{y_{t}} {s_{t-m}}}+( 1-\alpha) ( \ell_{t-1}+b_{t-1} ) ℓt=αst−myt+(1−α)(ℓt−1+bt−1)
b t = β ∗ ( ℓ t − ℓ t − 1 ) + ( 1 − β ∗ ) b t − 1 b_{t}=\beta^{*} ( \ell_{t}-\ell_{t-1} )+( 1-\beta^{*} ) b_{t-1} bt=β∗(ℓt−ℓt−1)+(1−β∗)bt−1
s t = γ y t ( ℓ t − 1 + b t − 1 ) + ( 1 − γ ) s t − m s_{t}=\gamma{\frac{y_{t}} {( \ell_{t-1}+b_{t-1} )}}+( 1-\gamma) s_{t-m} st=γ(ℓt−1+bt−1)yt+(1−γ)st−m
(三) 阻尼趋势
Holt-Winters 可以在加法和乘法季节性模型中引入阻尼(Damping)趋势。阻尼趋势能够使模型在预测未来趋势时更加稳健,避免趋势无限延伸,适用于那些趋势可能逐渐趋于稳定的时间序列数据,该方法结合了季节性和趋势的平滑,并通过阻尼因子 𝜙(0<𝜙<1) 控制趋势的持续性,将 𝜙 引入到趋势分量中,使得未来的趋势贡献逐渐减小。这样,随着预测期的增加,趋势的影响力会逐渐减弱,从而避免过度延伸。
结合了阻尼趋势的乘法季节性的预测方程为:
y ^ t + h ∣ t = [ ℓ t + ( ϕ + ϕ 2 + ⋯ + ϕ h ) b t ] s t + h − m ( k + 1 ) \hat{y}_{t+h | t}=\left[ \ell_{t}+( \phi+\phi^{2}+\cdots+\phi^{h} ) b_{t} \right] s_{t+h-m ( k+1 )} y^t+h∣t=[ℓt+(ϕ+ϕ2+⋯+ϕh)bt]st+h−m(k+1)
ℓ t = α ( y t s t − m ) + ( 1 − α ) ( ℓ t − 1 + ϕ b t − 1 ) \ell_{t}=\alpha\left( \frac{y_{t}} {s_{t-m}} \right)+\left( 1-\alpha\right) \left( \ell_{t-1}+\phi b_{t-1} \right) ℓt=α(st−myt)+(1−α)(ℓt−1+ϕbt−1)
b t = β ∗ ( ℓ t − ℓ t − 1 ) + ( 1 − β ∗ ) ϕ b t − 1 b_{t}=\beta^{*} \left( \ell_{t}-\ell_{t-1} \right)+( 1-\beta^{*} ) \phi b_{t-1} bt=β∗(ℓt−ℓt−1)+(1−β∗)ϕbt−1
s t = γ ( y t ℓ t − 1 + ϕ b t − 1 ) + ( 1 − γ ) s t − m s_{t}=\gamma\left( {\frac{y_{t}} {\ell_{t-1}+\phi b_{t-1}}} \right)+( 1-\gamma) s_{t-m} st=γ(ℓt−1+ϕbt−1yt)+(1−γ)st−m
二、Holt Winters算法优缺点
优点
1、Holt-Winters 方法能够有效捕捉和建模时间序列中的季节性变化,适用于具有周期性波动的数据。
2、通过平滑参数的设置,Holt-Winters 方法能够动态调整对趋势和季节性的估 计,适应时间序列数据的变化。
3、模型中包含的参数(水平、趋势、季节性)易于解释,便于理解时间序列的组成部分。
4、在短期预测方面,Holt-Winters 方法通常能提供较高的准确性。
缺点
平滑参数的选择对模型性能有很大影响,通常需要通过经验或交叉验证来优化这些参数,增加了模型设置的复杂性。
在长周期时间序列的预测中,Holt-Winters 方法可能会产生不切实际的趋势,特别是没有阻尼的情况下,可能导致长期预测的结果不稳定。
三、Python代码和Sentosa_DSML社区版算法实现对比
(一) 数据读入和统计分析
1、python代码实现
#导入需要的库
import os
import pandas as pd
import numpy as np
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
from matplotlib import rcParams
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScalerfile_path = r'.\每月香槟销量.csv'#文件路径
df = pd.read_csv(file_path, header=0)
print("原始数据前5行:")
print(df.head())>>原始数据前5行:Month Perrin Freres monthly champagne sales millions ?64-?72
0 1964-01 2815.0
1 1964-02 2672.0
2 1964-03 2755.0
3 1964-04 2721.0
4 1964-05 2946.0 df = df.rename(columns={'Month': '月份','Perrin Freres monthly champagne sales millions ?64-?72': '香槟销量'
})print("\n修改列名后的数据前5行:")
print(df.head())>>修改列名后的数据前5行:月份 香槟销量
0 1964-01 2815.0
1 1964-02 2672.0
2 1964-03 2755.0
3 1964-04 2721.0
4 1964-05 2946.0
完成数据读入后,对数据进行统计分析,统计数据分布图,计算每一列数据的极值、异常值等结果。代码如下:
stats_df = pd.DataFrame(columns=['列名', '数据类型', '最大值', '最小值', '平均值', '非空值数量', '空值数量','众数', 'True数量', 'False数量', '标准差', '方差', '中位数', '峰度', '偏度','极值数量', '异常值数量'
])def detect_extremes_and_outliers(column, extreme_factor=3, outlier_factor=5):q1 = column.quantile(0.25)q3 = column.quantile(0.75)iqr = q3 - q1lower_extreme = q1 - extreme_factor * iqrupper_extreme = q3 + extreme_factor * iqrlower_outlier = q1 - outlier_factor * iqrupper_outlier = q3 + outlier_factor * iqrextremes = column[(column < lower_extreme) | (column > upper_extreme)]outliers = column[(column < lower_outlier) | (column > upper_outlier)]return len(extremes), len(outliers)for col in df.columns:col_data = df[col]dtype = col_data.dtypemax_value = col_data.max() if np.issubdtype(dtype, np.number) else Nonemin_value = col_data.min() if np.issubdtype(dtype, np.number) else Nonemean_value = col_data.mean() if np.issubdtype(dtype, np.number) else Nonenon_null_count = col_data.count()null_count = col_data.isna().sum()mode_value = col_data.mode().iloc[0] if not col_data.mode().empty else Nonetrue_count = col_data[col_data == True].count() if dtype == 'bool' else Nonefalse_count = col_data[col_data == False].count() if dtype == 'bool' else Nonestd_value = col_data.std() if np.issubdtype(dtype, np.number) else Nonevar_value = col_data.var() if np.issubdtype(dtype, np.number) else Nonemedian_value = col_data.median() if np.issubdtype(dtype, np.number) else Nonekurtosis_value = col_data.kurt() if np.issubdtype(dtype, np.number) else Noneskew_value = col_data.skew() if np.issubdtype(dtype, np.number) else Noneextreme_count, outlier_count = detect_extremes_and_outliers(col_data) if np.issubdtype(dtype, np.number) else (None, None)new_row = pd.DataFrame({'列名': [col],'数据类型': [dtype],'最大值': [max_value],'最小值': [min_value],'平均值': [mean_value],'非空值数量': [non_null_count],'空值数量': [null_count],'众数': [mode_value],'True数量': [true_count],'False数量': [false_count],'标准差': [std_value],'方差': [var_value],'中位数': [median_value],'峰度': [kurtosis_value],'偏度': [skew_value],'极值数量': [extreme_count],'异常值数量': [outlier_count]})stats_df = pd.concat([stats_df, new_row], ignore_index=True)print(stats_df)>> 列名 数据类型 最大值 最小值 ... 峰度 偏度 极值数量 异常值数量
0 月份 object NaN NaN ... NaN NaN None None
1 香槟销量 float64 13916.0 1413.0 ... 2.702889 1.639003 3 0rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['SimHei']output_dir = r'.\holtwinters'#选择路径if not os.path.exists(output_dir):os.makedirs(output_dir)for col in df.columns:plt.figure(figsize=(10, 6))df[col].dropna().hist(bins=30)plt.title(f"{col} - 数据分布图")plt.ylabel("频率")file_name = f"{col}_数据分布图.png"file_path = os.path.join(output_dir, file_name)plt.savefig(file_path)plt.close()

2、Sentosa_DSML社区版实现
首先,进行数据读入,利用文本算子直接对数据进行读取,选择数据所在路径,

同时,可以在文本算子的删除和重命名配置中修改列名或者删除列,这里将列明分别修改为’月份’和 ‘香槟销量’。

点击应用,右击预览可以查看数据。

接着,利用描述算子即可对数据进行统计分析,得到每一列数据的数据分布图、极值、异常值等结果。连接描述算子,右侧设置极值倍数为3,异常值倍数为5。

右击执行,可以得到结果如下:

(二) 数据预处理
1、python代码实现
#数据预处理
for col in df.columns:print(f"列名: {col}, 数据类型: {df[col].dtype}")>>列名: 月份, 数据类型: object
列名: 香槟销量, 数据类型: float64df = df.dropna()
df['月份'] = pd.to_datetime(df['月份'], format='%Y-%m', errors='coerce') df['香槟销量'] = pd.to_numeric(df['香槟销量'], errors='coerce')
df = df.dropna(subset=['香槟销量'])
df['香槟销量'] = df['香槟销量'].astype(int)for col in df.columns:print(f"列名: {col}, 数据类型: {df[col].dtype}")print(df)
>>列名: 月份, 数据类型: datetime64[ns]
列名: 香槟销量, 数据类型: int32filtered_df1 = df[df['月份'] <= '1971-09']
print(filtered_df1)
>> 月份 香槟销量
0 1964-01-01 2815
1 1964-02-01 2672
2 1964-03-01 2755
3 1964-04-01 2721
4 1964-05-01 2946filtered_df2 = df[df['月份'] > '1971-09']
print(filtered_df2)>> 月份 香槟销量
93 1971-10-01 6981
94 1971-11-01 9851
95 1971-12-01 12670
96 1972-01-01 4348
97 1972-02-01 3564filtered_df1.set_index('月份', inplace=True)
resampled_df1 = filtered_df1['香槟销量'].resample('MS').bfill()print(resampled_df1)>> 月份 香槟销量
1964-01-01 2815
1964-02-01 2672
1964-03-01 2755
1964-04-01 2721
1964-05-01 2946...
1971-05-01 5010
1971-06-01 4874
1971-07-01 4633
1971-08-01 1659
1971-09-01 5951
2、Sentosa_DSML社区版实现
首先,连接格式算子对数据进行格式修改,将月份数据格式由String类型修改为Data类型。

其次,对数据进行过滤,将小于等于1971-09的数据作为训练和验证数据集,条件为大于1971-09的数据用于与时序预测数据做对比。可以利用两个过滤算子实现,算子右侧表格中属性“表达式”为spark sql表达式。
第一个过滤算子,条件为月份<=‘1971-09’,

第二个过滤算子条件为月份>‘1971-09’,右击预览即可查看过滤数据。

连接时序数据清洗算子,对用于模型训练的数据进行预处理,设置时间列为月份(时间列必须为Data/DataTime类型数据),选择采样频率使时间列数据时间相隔为1月,对香槟销量列以线性方式进行数据填充。

(三) 模型训练和模型评估
1、python代码实现
#模型定义
model = ExponentialSmoothing(resampled_df1, trend='add', seasonal='mul', seasonal_periods=12,damped_trend=True)
fit = model.fit(damping_slope=0.05)#预测
forecast = fit.predict(start=len(resampled_df1), end=len(resampled_df1) + 11
)residuals = resampled_df1 - fit.fittedvalues
residual_std = np.std(residuals)
upper_bound = forecast + 1.96 * residual_std
lower_bound = forecast - 1.96 * residual_stdresults_df = pd.DataFrame({'预测值': forecast,'上限': upper_bound,'下限': lower_bound
})
print(results_df)
>> 月份 预测值 上限 下限
1971-10-01 7143.862498 8341.179324 5946.545672
1971-11-01 10834.141889 12031.458716 9636.825063
1971-12-01 13831.428845 15028.745671 12634.112019
1972-01-01 4054.821228 5252.138054 2857.504402
1972-02-01 3673.653407 4870.970233 2476.336580#模型评估
y_true = resampled_df1.values
y_pred = fit.fittedvalues.valuesdef evaluate_model(y_true, y_pred, model_name="Holt-Winters"):r_squared = r2_score(y_true, y_pred)mae = mean_absolute_error(y_true, y_pred)mse = mean_squared_error(y_true, y_pred)rmse = mean_squared_error(y_true, y_pred, squared=False)print(f"模型评估结果 ({model_name}):")print(f"{'-' * 40}")print(f"R² (决定系数): {r_squared:.4f}")print(f"MAE (平均绝对误差): {mae:.4f}")print(f"MSE (均方误差): {mse:.4f}")print(f"RMSE (均方根误差): {rmse:.4f}")print(f"{'-' * 40}\n")return {"R²": r_squared,"MAE": mae,"RMSE": rmse,"MSE": mse}evaluation_results = evaluate_model(y_true, y_pred, model_name="Holt-Winters")>>模型评估结果 (Holt-Winters):
----------------------------------------
R² (决定系数): 0.9342
MAE (平均绝对误差): 451.4248
MSE (均方误差): 402168.8567
RMSE (均方根误差): 634.1678
2、Sentosa_DSML社区版实现
在时序数据清洗算子后,连接HoltWinters算子,HoltWinters算子根据现有的时间序列对应的数据,预测未来时间的数据。算子的输入数据支持多种key键,但必须是满足相同key键下时间列间隔为固定数值,且数值列非空的时序数据,建议是时序数据清洗算子处理后的数据。
这里将时间列设为月份列,数据列设为香槟销量列,预测数量和周期性参数设置为12,分析频率为month,模型类型为Multiplicative,显著性水平alpha设置为0.05。

模型连接时间序列模型评估算子,右击执行,可以查看评估结果。


(四) 模型可视化
1、python代码实现
#可视化
rcParams['font.family'] = 'sans-serif'
rcParams['font.sans-serif'] = ['SimHei'] plt.figure(figsize=(12, 6))
plt.plot(resampled_df1, label='实际销量', color='blue')
plt.plot(fit.fittedvalues, label='拟合值', color='orange')
plt.plot(forecast, label='预测销量', color='green')
plt.title('Holt-Winters 方法预测香槟销量')
plt.xlabel('时间')
plt.ylabel('香槟销量')
plt.axvline(x=resampled_df1.index[-1], color='red', linestyle='--', label='预测起始点')
plt.legend()
plt.show()plt.figure(figsize=(12, 6))
plt.plot(resampled_df1.index, resampled_df1, label='实际值', color='blue')
plt.plot(results_df.index, results_df['预测值'], label='预测值', color='orange')
plt.fill_between(results_df.index, results_df['下限'], results_df['上限'], color='lightgray', alpha=0.5, label='95% 置信区间')
plt.title('Holt-Winters 预测与置信区间')
plt.xlabel('时间')
plt.ylabel('香槟销量')
plt.legend()
plt.show()filtered_forecast_df = results_df[results_df.index > pd.Timestamp('1971-09-01')]
print(filtered_forecast_df)
>> 月份 预测值 上限 下限
1971-10-01 7143.862498 8341.179324 5946.545672
1971-11-01 10834.141889 12031.458716 9636.825063
1971-12-01 13831.428845 15028.745671 12634.112019
1972-01-01 4054.821228 5252.138054 2857.504402
1972-02-01 3673.653407 4870.970233 2476.336580results_df = results_df.drop(columns=['上限', '下限'])
print(results_df)
>> 月份 预测值
1971-10-01 7143.862498
1971-11-01 10834.141889
1971-12-01 13831.428845
1972-01-01 4054.821228
1972-02-01 3673.653407
1972-03-01 4531.419772
1972-04-01 4821.096141results_df.index.name = '月份'
merged_df = pd.merge(filtered_df2, results_df, left_on='月份', right_index=True, how='left')print(merged_df)
>> 月份 香槟销量 预测值
93 1971-10-01 6981 7143.862498
94 1971-11-01 9851 10834.141889
95 1971-12-01 12670 13831.428845
96 1972-01-01 4348 4054.821228
97 1972-02-01 3564 3673.653407scaler = StandardScaler()
merged_df[['香槟销量', '预测值']] = scaler.fit_transform(merged_df[['香槟销量', '预测值']])plt.figure(figsize=(12, 6))
plt.plot(merged_df['月份'], merged_df['香槟销量'], label='香槟销量', color='blue')
plt.plot(merged_df['月份'], merged_df['预测值'], label='香槟预测销量', color='orange')
plt.title('时序图')
plt.xlabel('时间')
plt.ylabel('香槟销量')
plt.legend()
plt.show()



2、Sentosa_DSML社区版实现
为了对比原始数据和预测数据,首先,利用过滤算子对HoltWinters模型预测数据进行过滤,过滤条件为月份>‘1971-09’。

右击预览可以查看数据过滤结果。

其次,连接删除和重命名算子,将需要的时间列和预测结果列保留,其余列删除。

应用完成后右击即可查看处理结果。

然后,连接合并算子,将原始数据和预测数据进行合并,分为关键字合并和顺序合并两种,这里使用关键字合并,用于合并的关键字为月份列,合并方式选择左连接。

右击预览可以得到合并算子的处理结果。

再连接图表分析中的时序图算子,“序列”可以选择多列,当序列为多列时需要配置“每个序列是否单独显示”,

右击执行后可以得到可视化结果,右上方可以进行下载等操作,鼠标移动可以查看当前位置的数据信息,下方可以滑动调整数据的时序区间。

对于HoltWinters模型的预测结果,直接连接时序图算子进行图表分析,采用序列模式,对香槟销量实际值和预测值进行对比。

右击执行得到结果如下所示:

采用时间序列模型模式对于HoltWinters模型的预测结果进行图表分析,属性设置如右侧所示。

右击执行得到结果,其中,实心点数据表示原始真实值,实线表示对原始数据的拟合数据,空心虚线表示预测数据,阴影边界的上下虚线分别表示置信区间的预测上限和下限。

四、总结
相比传统代码方式,利用Sentosa_DSML社区版完成机器学习算法的流程更加高效和自动化,传统方式需要手动编写大量代码来处理数据清洗、特征工程、模型训练与评估,而在Sentosa_DSML社区版中,这些步骤可以通过可视化界面、预构建模块和自动化流程来简化,有效的降低了技术门槛,非专业开发者也能通过拖拽和配置的方式开发应用,减少了对专业开发人员的依赖。
Sentosa_DSML社区版提供了易于配置的算子流,减少了编写和调试代码的时间,并提升了模型开发和部署的效率,由于应用的结构更清晰,维护和更新变得更加容易,且平台通常会提供版本控制和更新功能,使得应用的持续改进更为便捷。
为了非商业用途的科研学者、研究人员及开发者提供学习、交流及实践机器学习技术,推出了一款轻量化且完全免费的Sentosa_DSML社区版。以轻量化一键安装、平台免费使用、视频教学和社区论坛服务为主要特点,能够与其他数据科学家和机器学习爱好者交流心得,分享经验和解决问题。文章最后附上官网链接,感兴趣工具的可以直接下载使用
https://sentosa.znv.com/

相关文章:

【机器学习(十)】时间序列案例之月销量预测分析—Holt-Winters算法—Sentosa_DSML社区版
文章目录 一、Holt-Winters算法原理(一) 加法模型(二) 乘法模型(三) 阻尼趋势 二、Holt Winters算法优缺点优点缺点 三、Python代码和Sentosa_DSML社区版算法实现对比(一) 数据读入和统计分析(二) 数据预处理(三) 模型训练和模型评估(四) 模型可视化 四、总结 一、Holt-Winters…...

Webpack优化问题
目录 打包流程swcthread-loaderhash升级插件 打包流程 webpack 的打包流程大致可以分为以下几个步骤: 初始化:webpack 通过配置文件和 Shell 参数,初始化参数,确定入口文件、输出路径、加 载器、插件等信息。接下来读取配置文件…...

yjs10——pandas的基础操作
1.pandas读入文件——pd.read_cvs() data pd.read_csv("E:/机器学习/data/salary.csv") 注意:1.是pd.read_cvs,不要顺手写成np.read_cvs 2.路径的斜杠方向是/,不是\,如果直接从电脑粘贴路径,路径写法是\&am…...

Squaretest单元测试辅助工具使用
1、idea安装插件 Squaretest 然后关掉idea 2、安装字节码软件(jclasslib) 3、找到idea里面的Squaretest安装目录 找到包含TestStarter的jar包 4、打开 com.squaretest.c.f 打开后选择常量池 5、找到第16个修改 Long value值,修改的数字即为使…...

MFU简介
1、缩写 MFU - Mask Field Utilization(光刻掩膜版有效利用比例) GDPW - Gross Die Per Wafer,每张wafer上die的数量 2、什么是MASK 在光刻机中,光源(紫外光、极紫外光)透过mask曝光在晶圆上形成图…...

十分钟实现内网连接,配置frp
十分钟实现内网连接,配置frp 一.frp是什么?其实是一款实现外网连接内网的一个工具,个人理解,说白了就像是teamviwer一样,外网能访问内网。 利用处于内网或防火墙后的机器,对外网环境提供 http 或 https 服…...

解决MySQL命令行中出现乱码问题
在MySQL命令行中遇到乱码问题通常是由于字符编码设置不正确导致的。以下是一些解决步骤: 1. **检查和设置字符集**: 首先,您需要确保MySQL服务器、客户端和数据库使用的是正确的字符集。您可以通过执行以下命令来查看当前的字符集设置&…...
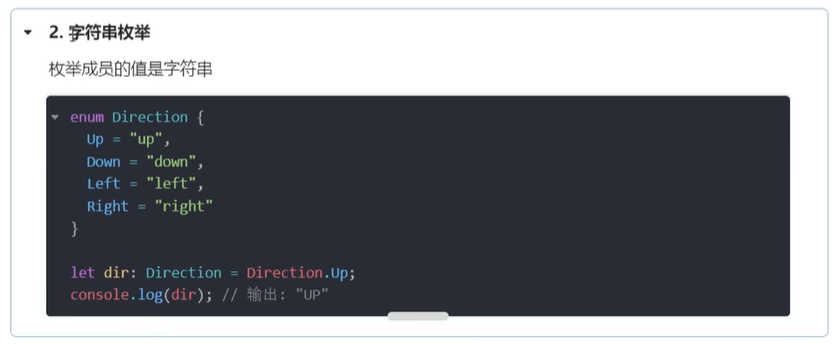
TS系列(7):知识点汇总
你好,我是沐爸,欢迎点赞、收藏、评论和关注。 一、TS是什么? TypeScript 由微软开发,是基于 JavaScript 的一个扩展语言。TypeScript 包含 JavaScript 的所有内容,是 JavaScript 的超集。TypeScript 增加了静态类型检…...

Unity 查看Inspectors组件时严重掉帧
遇到一个问题,就是运行一个脚本的时候,只要我查看它的Inspectors,就会严重掉帧。 原本是30fps,只要查看这个组件,就掉到5fps。 这还真有点像波粒二象性,一观察就会掉帧,不观察就正常。 using…...
:多态与断言【重要】)
golang学习笔记23-面向对象(五):多态与断言【重要】
本节也是GO核心部分,很重要。 注:由于导包语句已经在19讲(笔记19:面向对象的引入)展示过了,所以这里就不展示了。 一、多态(Polymorphism) 变量(实例)具有多…...

RabbitMQ基础知识
1.1 什么是MQ? 消息队列(Message Queue),是基础数据结构中 “先进先出” 的一种数据结构。 一般用来解决应用解耦、异步消息、流量削峰等问题,实现高性能、高可用、可伸缩和最终一致性架构。 RabbitMQ可以理解为一个邮箱&#x…...

基于Python大数据的音乐推荐及数据分析可视化系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码 精品专栏:Java精选实战项目…...

安达发|太阳能设备行业APS计划排程软件能解决哪些问题
在当今快速发展的太阳能设备行业中,高级计划与排程(APS)软件成为了企业优化生产流程、提高生产效率和满足市场需求的关键工具。APS软件通过集成先进的算法和数据分析技术,为企业提供了一个全面的生产计划和排程解决方案。本文将探…...

CaChe的基本原理
目录 一、Cache的定义与结构 二、Cache的工作原理 三、Cache的映射与替换策略 四、Cache的写操作处理 Cache,即高速缓冲存储器,是计算机系统中位于CPU与主存之间的一种高速存储设备。它的主要作用是提高CPU对存储器的访问速度,从而优化系…...

数据结构-栈(理解版)
一、栈的定义 相信大家对于栈或多或少有一些了解,可能大多数人会告诉你栈是一种先进后出的数据结构。这其实说了跟没说一样(❁◡❁)!当然(last in,first out)是栈最有特色的性质。 这里可以给大家一些比较好理解的例…...

NAND Flash虚拟层初始化
在整个NAND Flash初始化过程中,其主要过程由NAND_Init()函数来完成的,因此以下以NAND_Init()函数作为入口,对NAND Flash虚拟层初始化进行全面分析: NAND_Init()NAND_PhyInit()FMT_Init()FMT_FormatNand()LML_Init() NAND_Init()函数首先调用NAND_PhyInit()函数…...

zabbix7.0监控linux主机案例详解
前言 服务端配置 链接: rocky9.2部署zabbix服务端的详细过程 环境 主机ip应用zabbix-server192.168.10.11zabbix本体zabbix-client192.168.10.12zabbix-agent zabbix-server(服务端已配置) 具体实现过程 zabbix-client配置 安装zabbix-agent 添加扩展包 dnf -y instal…...

2024重生之回溯数据结构与算法系列学习(10)【无论是王道考研人还是IKUN都能包会的;不然别给我家鸽鸽丢脸好嘛?】
欢迎各位彦祖与热巴畅游本人专栏与博客 你的三连是我最大的动力 以下图片仅代表专栏特色 专栏跑道一 ➡️ MYSQL REDIS Advance operation 专栏跑道二➡️ 24 Network Security -LJS 专栏跑道三 ➡️HCIP;H3C-SE;CCIP——LJS[华为、华三、思科高级网络]…...

django drf 过滤器
排序 代码: from rest_framework.generics import ListAPIView from rest_framework.filters import OrderingFilterclass TestListAPIView(ListAPIView):queryset models.Course.objects.filter(is_deleteFalse).all()serializer_class serializers.TestModelS…...

蓝桥杯—STM32G431RBT6(RTC时钟获取时间和日期)
一、RTC是什么,有什么用? 在 STM32 中,RTC(Real-Time Clock,实时时钟)主要有以下作用: 时间保持:即使在系统断电情况下,也能持续记录时间。(需要纽扣电池供电…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
