【数据结构】什么是平衡二叉搜索树(AVL Tree)?
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
📌AVL树的概念
📌AVL树的操作
🎏AVL树的插入操作
↩️右单旋
↩️↪️右左双旋
↪️↩️左右双旋
↪️左单旋
🎏AVL树的删除操作
结语
📌AVL树的概念
我们之前一起学习过二叉搜索树,知道它具有较好的搜索性能, 但是普通的二叉搜索树会有一个问题,那就是它可能会因为输入的值不够随机,也可能因为经过某些插入或删除的操作,导致其失去平衡退化为单支树并导致搜索效率降低的情况, 如下不平衡搜索树:
可以发现,如果搜索二叉树退化到这样极端的不平衡状态,其搜索效率就会大大降低, 时间复杂度会从
退化到
.为了解决这种情况,我们将引入AVL树的概念.
AVL树是一个 “加上了额外平衡条件” 的二叉搜索树。其平衡条件的建立是为了确保整棵树的深度为
。直观上的最佳平衡条件是每个节点的左右子树有着相同的高度,但这未免太过严苛,我们很难插入新元素而又保持这样的平衡条件。AVL树于是退而求其次,要求任何节点的左右子树高度相差最多1。这是一个较弱的条件,但仍能够保证“对数深度(logarithmic depth)”平衡状态。
因此, AVL树是一种二叉搜索树, 其中每一个结点的左子树和右子树的高度差至多等于1。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF(Balance Factor), 那么平衡二叉树上所有结点的平衡因子只可能是-1/ 0/ 1.
📌AVL树的操作
🎏AVL树的插入操作
我们知道,对于一颗AVL树而言,新插入的结点是很有可能破坏其平衡结构的,如:
那么AVL树是如何解决这种情况的呢?下面我将通过模拟一组AVL树结点的插入来讲清楚AVL树是如何维持其平衡特性的.
下面我们将以这组数据为例,详细剖析一下AVL树维持其平衡的插入过程:
14 9 5 17 11 12 7 19 16 27
首先我们插入第一个结点14:
然后我们插入第二个结点9:
此时AVL树仍然是平衡状态,然后我们插入下一个结点5:
可以看到,插入结点5之后,AVL树的根节点14就已经不满足平衡搜索二叉树的条件了,即它左子树的高度减去右子树的高度已经大于1,因此我们下面就要运用AVL树对不平衡的第一种处理方式,也就是右单旋:
↩️右单旋
右单旋处理应用的情况为:
- 失衡结点平衡因子 = 2
- 失衡结点左孩子平衡因子 = 1
右单旋的处理操作步骤为:
- 将失衡结点左孩子的右子树链接到失衡结点的左孩子的位置
- 将失衡结点链接到失衡结点左孩子的右孩子位置
所以我们下面采取右单旋的方式使AVL树重新平衡, 因为失衡结点14的左孩子9并没有右孩子,所以我们可以直接将失衡结点14链接到失衡结点左孩子9的右孩子位置, 右单旋示意图如下:
经过右单旋操作之后,我们得到的AVL树就又重新满足平衡二叉搜索树了:
接下来我们继续插入新结点17:
再继续插入新结点11:
再继续插入新结点12:
可以看到,插入结点12之后,AVL树的根节点9就已经不满足平衡搜索二叉树的条件了,即它左子树的高度减去右子树的高度已经成了-2,因此我们下面就要运用AVL树对不平衡的第二种处理方式,也就是右左双旋:
↩️↪️右左双旋
右左双旋处理应用的情况为:
- 失衡结点平衡因子 = -2
- 失衡结点右孩子平衡因子 = 1
右左双旋的处理操作步骤为:
- 将失衡结点的右孩子右单旋
- 再将失衡结点左单旋
所以我们下面采取右左双旋的方式使AVL树重新平衡, 我们先将失衡结点9的右孩子14进行右单旋, 再将失衡结点9进行左单旋,右左双旋操作示意图如下:
经过右左双旋操作之后,我们得到的AVL树就又重新满足平衡二叉搜索树了:
我们继续插入新结点7:
可以看到,插入结点7之后,AVL树的节点9就已经不满足平衡搜索二叉树的条件了,即它左子树的高度减去右子树的高度已经成了2,因此我们下面就要运用AVL树对不平衡的第三种处理方式,也就是左右双旋:
↪️↩️左右双旋
左右双旋处理应用的情况为:
- 失衡结点平衡因子 = 2
- 失衡结点左孩子平衡因子 = -1
左右双旋的处理操作步骤为:
- 将失衡结点的左孩子左单旋
- 再将失衡结点右单旋
所以我们下面采取左右双旋的方式使AVL树重新平衡, 我们先将失衡结点9的左孩子5进行左单旋, 再将失衡结点9进行右单旋,左右双旋操作示意图如下:
经过左右双旋操作之后,我们得到的AVL树就又重新满足平衡二叉搜索树了:
然后我们继续插入新结点19:
继续插入新结点16:
最后插入结点27:
可以看到,插入结点27之后我们发现AVL树的根节点11和其右孩子14都失衡了.这个时候我们只需要调整距离新插入结点最近的失衡结点即可,调整完这个最近失衡结点之后,其余的祖先失衡结点会自动恢复平衡的。我们下面就要运用AVL树对不平衡的第四种处理方式,也就是左单旋:
↪️左单旋
左单旋处理应用的情况为:
- 失衡结点平衡因子 = -2
- 失衡结点右孩子平衡因子 = -1
左单旋的处理操作步骤为:
- 将失衡结点右孩子的左子树链接到失衡结点的右孩子的位置
- 将失衡结点链接到失衡结点右孩子的左孩子位置
所以我们下面采取左单旋的方式使AVL树重新平衡, 先将失衡结点14的右孩子17的右子树16链接到失衡结点14的右孩子的位置,再将失衡结点14链接到失衡结点右孩子17的左孩子位置, 左单旋示意图如下:
经过左单旋操作之后,我们得到的AVL树就完成了所有的插入操作并满足平衡二叉搜索树了:
在经历了四种旋转操作之后,我们将旋转的方式以及其对应的影响因子的特征总结如下:

🎏AVL树的删除操作
前面讲了AVL树的插入操作需要保证其不失衡, 对于AVL树的删除操作来说也一样, 同样需要保证其操作后树不失衡, 和插入操作不同的是, 删除操作可能会导致不只一次的失衡, 所以我们不能像插入那样只调节最近的失衡结点就行, 在删除时可以参考之前讲过的二叉搜索树的删除操作,但是AVL树在删除之后需要沿着祖先结点一直向上继续查找是否有结点失衡的情况,如果有,就需要进行旋转调整,其旋转规则和插入时我们总结的影响因子特征相同。
下图附上二叉搜索树的删除逻辑,有兴趣的朋友可以自行研究一下:
结语
希望这篇关于 平衡二叉搜索树(AVL树) 的博客能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【C++】STL标准模板库容器map
【C++】STL标准模板库容器set
【C++】模拟实现二叉搜索(排序)树
【数据结构】C语言实现链式二叉树(附完整运行代码)
【数据结构】什么是二叉搜索(排序)树?
【C++】模拟实现priority_queue(优先级队列)
【C++】模拟实现queue
【C++】模拟实现stack
【C++】模拟实现list
【C++】模拟实现vector
【C++】标准库类型vector
【C++】模拟实现string类
【C++】标准库类型string
【C++】构建第一个C++类:Date类
【C++】类的六大默认成员函数及其特性(万字详解)
【C++】什么是类与对象?

相关文章:

【数据结构】什么是平衡二叉搜索树(AVL Tree)?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌AVL树的概念 📌AVL树的操作 🎏AVL树的插入操作 ↩️右单旋 ↩️↪️右左双旋 ↪️↩️左右双旋 ↪️左单旋 🎏AVL树的删…...

ip的类型有多少种?我想做大数据需要使用哪一种
IP地址主要分为两种类型: IPv4(Internet Protocol version 4): 由32位二进制数组成,通常以四个十进制数表示(例如:192.168.1.1)。每个十进制数的范围是0到255。IPv4地址的总数量约为…...

位运算(6)_只出现一次的数字 II
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 位运算(6)_只出现一次的数字 II 收录于专栏【经典算法练习】 本专栏旨在分享学习算法的一点学习笔记,欢迎大家在评论区交流讨论💌 目录 …...

C#的Socket编程细节
目录 Socket中的Accept 步骤1:创建并绑定服务端套接字 步骤2:接受连接请求 步骤3:与客户端通信 步骤4:关闭套接字 注意事项 Socket中的Connected 使用Connected属性 客户端检查连接状态 服务端检查连接状态 注意事项 S…...

python三局两胜游戏
分为以下步骤实现这个功能 1、猜拳 2、机器产生数值 3、人去猜数字,定义剪刀石头布 4、控制机器产生,123程序运行的时候可能会出现一点玄学问题,就是,提示n1这一行不符合pep8然后报错,不用管,运行就可以&am…...

java:brew安装rabbitmq以及简单示例
什么是消息队列mq 可以看我之前写的这篇 消息队列MQ rabbitmq简介 RabbitMQ是由erlang语言开发,基于AMQP(Advanced Message Queue 高级消息队列协议)协议实现的消息队列,它是一种应用程序之间的通信方法,消息队列在…...

基于单片机跑步机控制系统设计
** 文章目录 前言概要功能设计设计思路 软件设计效果图 程序文章目录 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师,一名热衷于单片机技术探索与分享的博主、专注于 精通51/STM32/MSP430/AVR等单片机设计 主要对…...

【架构】efk日志监控
文章目录 一、EFK组件及其功能二、EFK日志监控的工作流程三、EFK日志监控的优势四、EFK日志监控的应用场景 推荐阅读 EFK日志监控是一种高效的日志管理解决方案,由Elasticsearch、Fluentd(或Logstash)和Kibana三个开源工具组成。以下是对EFK日…...
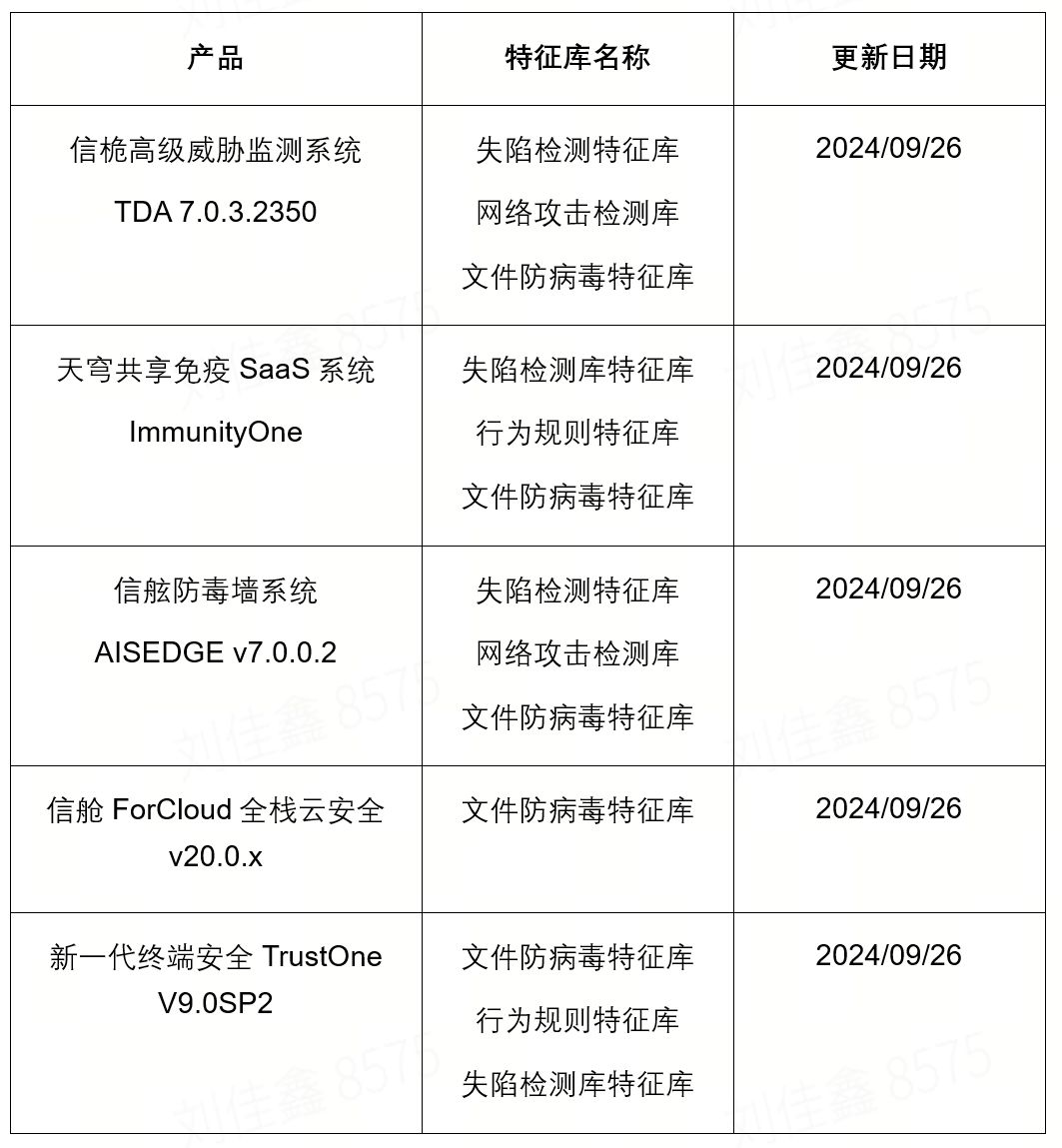
亚信安全发布第34期《勒索家族和勒索事件监控报告》
本周态势快速感知 本周全球共监测到勒索事件91起,近三周勒索事件数量较为稳定。从整体上看,Ransomhub是影响最严重的勒索家族;Play和ElDorado恶意家族也是两个活动频繁的恶意家族,需要注意防范。本周,土耳其公司巴克皮…...

如何在实际应用中使用回溯算法解决问题?
如何在实际应用中使用回溯算法解决问题? 回溯算法是一种强大的问题解决方法,它通过尝试不同的选择并在遇到不可行的情况时回退,以找到满足特定条件的解决方案。在实际应用中,回溯算法可以用于解决各种复杂的问题。本文将介绍如何在实际应用中使用回溯算法,并通过一些案例…...
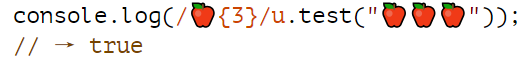
9. 正则表达式
编程工具和技术是以一种混乱、进化的方式生存和传播的。获胜的并不总是最好或最杰出的工具,而是那些在合适的利基市场中发挥足够好的功能,或者恰好与另一项成功的技术相结合的工具。 在本章中,我将讨论这样一种工具--正则表达式。正则表达式是…...

初始C++模板
1.泛型编程 1.1什么事泛型编程 在学习C语言时,我们时常会有这样的烦恼: 在针对每一种不同的类型变量进行函数传参或者是运算处理时,我们总是编写不同的函数或者是进行不同的处理,才能达到目的,这时,我们…...

建投数据自主研发相关系统获得欧拉操作系统及华为鲲鹏技术认证书
近日,经欧拉生态创新中心和华为技术有限公司测评,建投数据自主研发的投资项目管理系统、全面风险管理信息系统、商业不动产业务系统,完成了基于欧拉操作系统openEuler 22.03、华为鲲鹏Kunpeng 920(Taisha 200)的兼容性…...

node启动websocket保持后台一直运行
在 Node.js 中启动一个 WebSocket 服务器并使其在后台持续运行,你可以使用几种方法。下面是一种常见的方法,通过创建一个简单的 WebSocket 服务器并使用 node 命令直接运行它,同时确保它在后台运行。 1. 创建 WebSocket 服务器 首先&#x…...

CSS画出三角形的做法
引言: 在网页中,会有三角形的出现,我们脑海里会有很多想法,如何去实现他们,我来提供一种比较好玩的做法。 方法: 我们实现一个三角形,当然可以使用精灵图、或者iconfont的做法,这…...
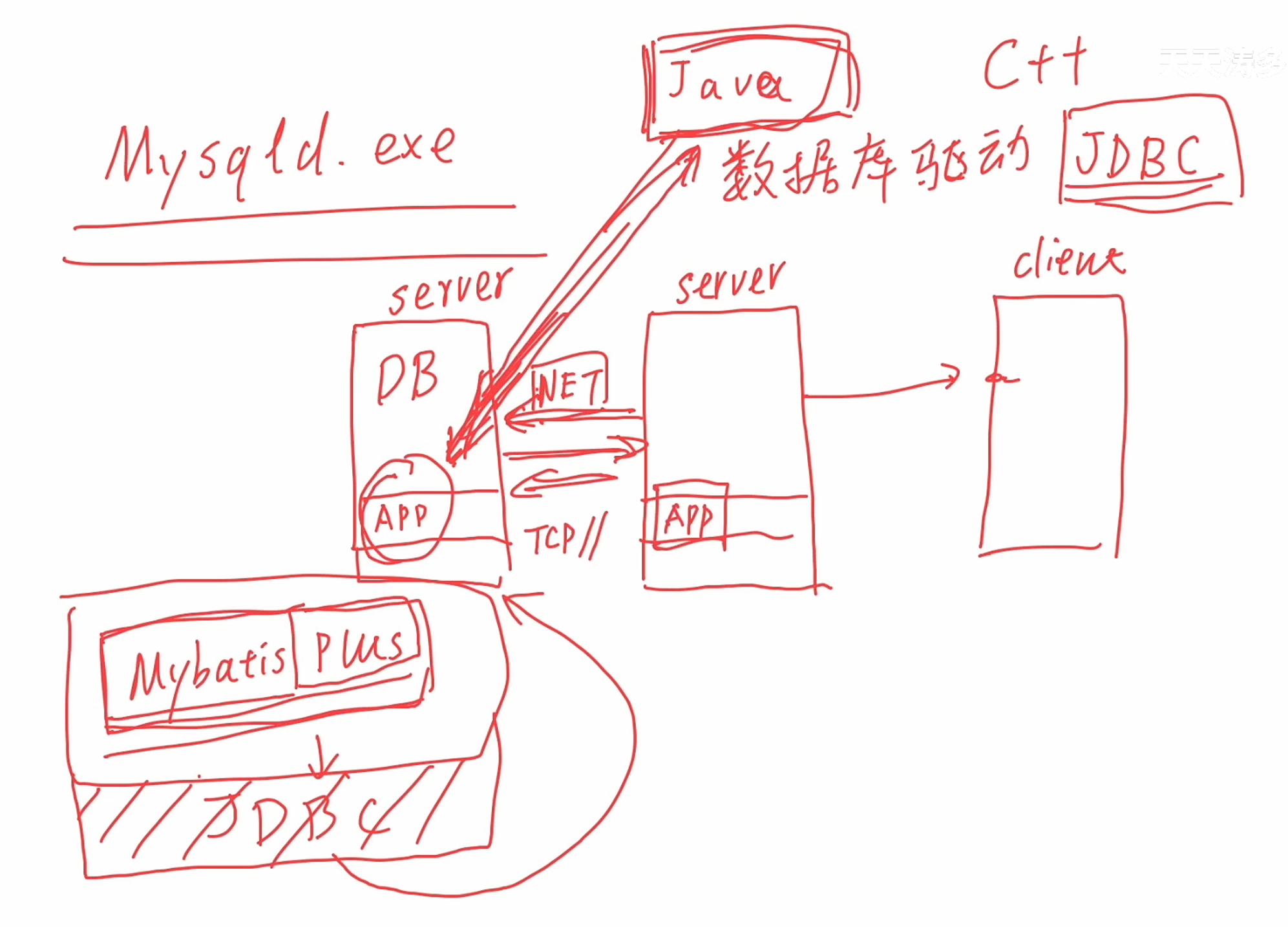
web开发(1)-基础
这是对b站课程的总结,后续可能会继续更 01 前后端分离介绍_哔哩哔哩_bilibili01 前后端分离介绍是Web应用开发-后端基础-基于Springboot框架的第1集视频,该合集共计29集,视频收藏或关注UP主,及时了解更多相关视频内容。https://w…...
)
python程序操作Windows系统中的软件如word等(是否可以成功操作待验证)
一、python打开word软件 在 Python 中可以使用python-docx库来操作 Word 文档,但如果你的需求是直接打开 Word 软件,你可以使用os模块和subprocess模块来实现。以下是示例代码: import os import subprocessdef open_word():word_path rC:…...

人工智能发展历程
发展历程 人工智能的发展可以追溯到20世纪30年代,当时数理逻辑的形式化和智能可计算思想开始构建计算与智能的关联概念。1943年,美国神经科学家麦卡洛克和逻辑学家皮茨共同研制成功了世界上首个人工神经网络模型——MP模型,这为现代人工智能…...

Flutter路由
路由作为一种页面切换的能力,非常重要。Flutter 中路由管理有几个重要的点。 Navigator 1.0:Flutter 早期路由系统,侧重于移动端 ,命令式编程风格,使用 Navigator.push() 和 Navigator.pop() 等方法来管理路由栈。 N…...

css预处理器less
CSS预处理器Less教程 CSS预处理器是一种扩展CSS功能的工具,它允许开发者使用变量、嵌套规则、混合(Mixins)、函数等高级特性,使CSS代码更加灵活、易于维护和扩展。Less是其中一种流行的CSS预处理器,它使用JavaScript编…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...





















