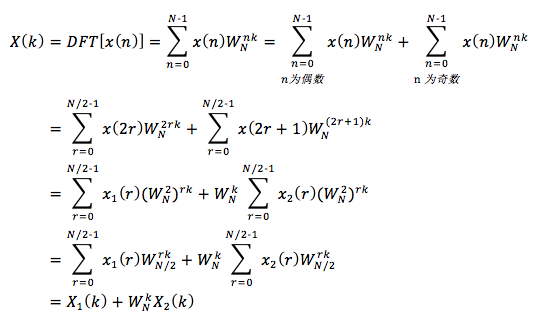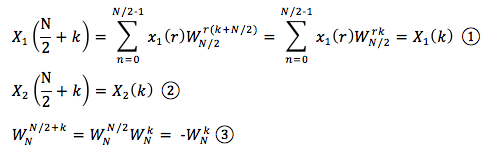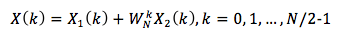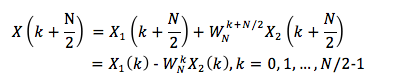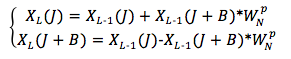信号处理快速傅里叶变换(FFT)的学习

FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。采样频率要大于信号频率的两倍。为了方便进行FFT运算，通常N取2的整数次方。

一、DFT

1.1 原理

定义（来自百科）：离散傅里叶变换（Discrete Fourier Transform，缩写为DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。在实际应用中通常采用快速傅里叶变换计算DFT。

DFT的公式是：设x(n)为M点的有限长序列，即在0≤n≤M-1内有值，则定义x(n)的N点（N≥M。当N＞M时，补N-M个零值点），离散傅里叶变化定义为

其中，为旋转因子（为方便编辑后续记作W(N, nk)，特此说明），其计算公式为，具有以下性质：

①周期性：W(N, nk) = W(N, (n+rN)k) = W(N, n(k+rN))，其中r问整数。

②共轭对称性：(W(N, nk))* = W(N, -nk)。

③可约性：W(N, nk) = W(mN, mnk)，W(N, nk) = W(N/m, nk/m)，其中m为整数，N/m为整数。

④特殊值：W(N, N/2) = -1；  W(N, (k+N/2)) = -W(N, k)；  

                  W(N, (N-k)n) = W(N, (N-n)k) = W(N, -nk)。

所以，在计算旋转因子的过程中可以适当的使用特殊值来提高运算的效率。

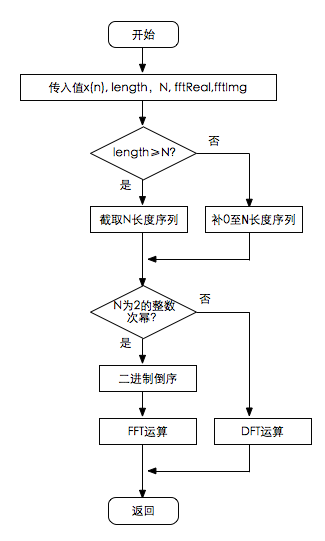
在计算DFT时，如果数据的点数够计算的点数，则截取计算点数长的数据进行DFT运算，否则将数据点个数补0至计算点个数，然后进行计算，举例如下（举例只是为了说明问题，没有按照编程语言的书写格式）。

比如：数据点数组为 dataArray = {1， 2， 3， 4，5}，可以看出数据长度为5。

如果要求做4点DFT运算，则只需截取前4个数作为运算数组进行运算即可，即为{1， 2， 3， 4}；

如果要求做8点DFT运算，则需在原数组后补三个0，使长度为8后再进行计算，计算数组为{1， 2， 3， 4，5，0，0，0}。

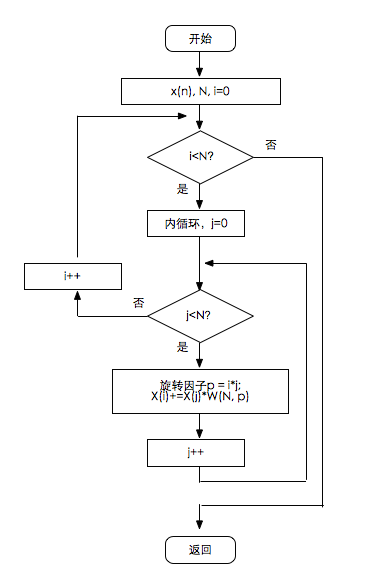
1.2 流程图

二、FFT

2.1 原理

设序列x(n)点数为N=2^L，L为整数。将N=2^L，先按照n的奇偶分为两组，

其中r = 0, 1, ..., N/2-1，x(2r) = x1(r)，x(2r-1) = x2(r)；

则可将DFT化为

由上式可以看出一个N点的DFT可以分为两个N/2点的DFT，按照上式右组合成N点DFT。但是这里的x1(r)、x2(r)以及X1(k)、X2(k)都是N/2点的序列，即r,k满足r,k=0, 1, ..., N/2-1。而X(k)却有N点，上式计算的只是X(k)的前半项数的结果，因此还需要计算后半项的值。

将①②③代入（式1），就可将X(k)表达为前后两部分：

前半部分，X(k)，当k=0, 1, ..., N/2-1

后半部分，X(k)，当k=N/2, ..., N-1

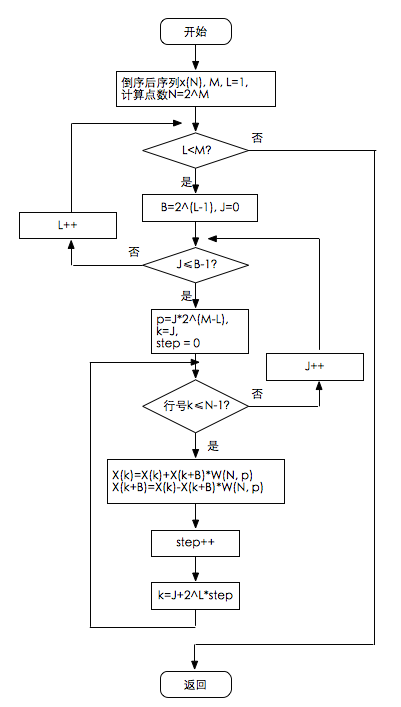
2.2 流程图

①FFT运算总流程图，包括

②根据（1）中推导的内容，FFT的流程图可化为

蝶形运算中又三层循环

第一层（最外层），完成M次迭代过程，即算出A0(k), A1(k), ..., Am(k)，其中k=0, 1, ..., N；A2(k)为蝶形运算第2级的结果，如A0(k)=x(k), Am(k)=X(k)；

第二层（中间层），完成旋转因子的变化，步进为2^L；

第三层（最里层），完成相同旋转因子的蝶形运算。

三、DFT与FFT

1.DFT的运算量

复数乘法次数为N*N，复数加法次数为N(N-1)，若N>>1，则这两者都近似为N*N，它随N增大为急速增大。改进途径：①利用旋转因子性质减小计算量；②由于运算量和N*N成正比，因而可将N点DFT分解成小点数的DFT，以减少运算量（点数越小，计算量越小）；③改为用FFT计算，复数乘法次数为(N/2)*log(2,N)。

2.FFT可分为按照时间抽选的基-2算法（库利-图基算法DIT-FFT）和按频率抽选的基-2算法（桑德-图基算法DIF-FFT）。

3.FFT计算原理

FFT的计算要求点数必须为2的整数次幂，如果点数不够用0补齐。例如计算{2，3，5，8，4}的8点FFT，需要补3个0后进行计算，如果计算该数组的5点FFT，则先计算8点FFT后截取前5个值即可（不提倡）。

四、蝴蝶运算

4.1 基本流程

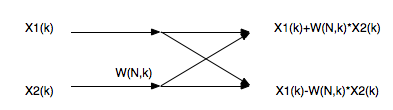
蝶形运算，符号表示如下图所示：

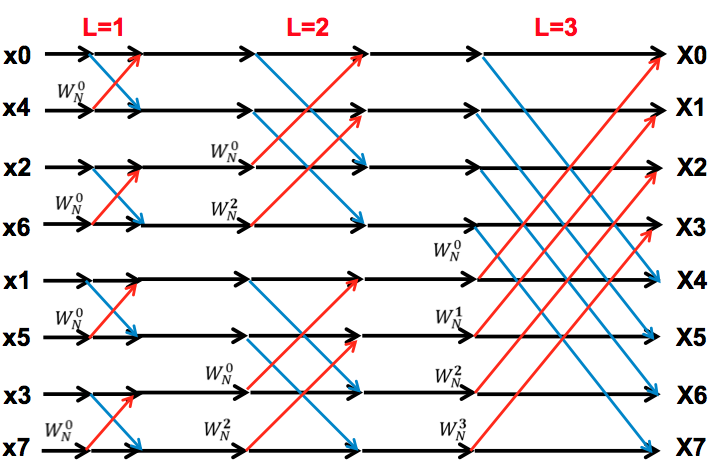
所以，FFT的蝶形运算图表示为（8点，2^3 = 8，运算级数最大为L=3）

在蝶形运算中变化规律由W(N, p)推导，其中N为FFT计算点数，J为下角标的值

        L = 1时，W(N, p) = W(N, J) = W(2^L, J)，其中J = 0;

        L = 2时，W(N, p) = W(N, J) = W(2^L, J)，其中J = 0, 1;

        L = 3时，W(N, p) = W(N, J) = W(2^L, J)，其中J = 0, 1, 2, 3;

所以，W(N, p) = W(2^L, J)，其中J = 0, 1, ..., 2^(L-1)-1

又因为2^L = 2^M*2^(L-M) = N*2^(L-M)，这里N为2的整数次幂，即N=2^M，

W(N, p) = W(2^L, J) = W(N*2^(L-M), J) = W(N, J*2^(M-L))

所以，p = J*2^(M-L)，此处J = 0, 1, ..., 2^(L-1)-1，当J遍历结束但计算点数不够N时，J=J+2^L，后继续遍历，直到计算点数为N时不再循环。

4.2 举例：N=8点的FFT计算

当L=2时，J = 0, 1两个值，因此p = J*2^(M-L) = 0, 2两个值，即旋转因子有两个值W(8, 0)和W(8, 2)，计算中两行之间的距离B = 2^(L-1)=2^(2-1)=2，

代入J=0, 1可求得X(0)、X(0+2)和X(1)、X(1+2)，即可求出第2级蝶形运算的X(0), X(1), X(2), X(3)，也就是求出一半，此时J加步进2^L=4，即J=J+2^L=4, 5，

再代入J=4, 5可求出X(4), X(4+2)和X(5), X(5+2)，即可求出第2级蝶形运算的X(4), X(5), X(6), X(7)，已经全部求出，J循环结束。

4.3 二进制倒序说明

前面数的排列顺序是进行二进制倒序后的排序。二进制倒序是指将某数转化为二进制表示，将最高位看做最低位、次高位看做次低位...以此类推，计算后的纸进行排序。例如3的二进制表示为011b（3=0*2^2+1*2+1），二进制倒序值为6（011b，最高位看做最低位...即6=0+1*2+1*2^2）

即0到7的二进制排序是：

       0,                4,                 2,                6,                 1,                5,                3,                7

000→000    001→100    010→010    011→110    100→001    101→101    110→011    111→111

五、从振幅或快速傅立叶变换到dB

从振幅或快速傅立叶变换到dB是一个涉及信号处理和单位转换的问题。

函数f(t)为一元连续函数，其傅里叶变换定义为：

其中，i为虚数单位。欧拉公式：

5.1 相关名词

1.振幅（Amplitude）：振幅是指信号的最大偏离值，表示信号的强度或能量大小。在信号处理中，振幅常用于描述波形的高低或振动的幅度。

2.dB（分贝）：分贝是一种用于表示信号强度或功率比例的对数单位。在信号处理中，分贝常用于描述信号的增益或衰减程度。分贝的计算公式为：dB = 10 * log10(P1/P0)，其中P1为信号的功率，P0为参考功率。当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，即用频响特性来表述即为-3dB点处即为截止频率，它是用来说明频率特性指标的一个特殊频率。

利用系统函数的模来表示电路的放大倍数，由于20lgA（ω）=-3dB，解得

A（ω）=10^-0.15=0.707945784≈1/√2，又因为A（ω）=|H（jω）|，则|H（jω）|^2=1/2

在高频端和低频端各有一个截止频率，分别称为上截止频率和下截止频率。两个截止频率之间的频率范围称为通频带。

5.2 物理意义理解

假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。

1.幅值：这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。

2.相位：而每个点的相位呢，就是在该频率下的信号的相位。

3.分辨率：第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。例如某点n所表示的频率为：Fn=(n-1)*Fs/N。由上面的公式可以看出，Fn所能分辨到频率为为Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。

4.表达式：假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=根号a*a+b*b，相位就是Pn=atan2(b,a)。根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：An/(N/2)*cos(2*pi*Fn*t+Pn)，即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号，是直流分量，幅度即为A1/N。

由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。

5.3 示例

假设我们有一个信号，它含有2V的直流分量，频率为50Hz、相位为-30度、幅度为3V的交流信号，以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下（式中cos参数为弧度，所以-30度和90度要分别换算成弧度）：

S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)

我们以256Hz的采样率对这个信号进行采样，总共采样256点。按照我们上面的分析，Fn=(n-1)*Fs/N，我们可以知道，每两个点之间的间距就是1Hz，第n个点的频率就是n-1。我们的信号有3个频率：0Hz、50Hz、75Hz，应该分别在第1个点、第50个点、第76个点上出现峰值，其它各点应该接近0。

	幅值	相位（弧度）	相位（角度）
直流分量	512/N =512/256 =2	\	\
50Hz	384/(N/2) =384/(256/2) =3	atan2(-192, 332.55) =-0.5236	(-0.5236)/pi =-30.0001
75Hz	192/(N/2) =192/(256/2) =1.5	atan2(192, 3.4315E-12) =1.5708	180*1.5708/pi =90.0002

（图片横坐标为第几个点，即Hz；纵坐标为模）

5.4 波特图

1、伯德图的定义

伯德图由对数幅频特性和对数相频特性两条曲线构成。 伯德图一般是由二张图组合而成， 伯德图由两张图组成：①G(jω)的幅值(以分贝，dB表示)-频率(以对数标度)对数坐标图，其上画有对数幅频曲线；②G(jω)的相角-频率(以对数标度)对数坐标图，其上画有相频曲线。 

对数幅值的标准表达式为20 lg|G(jω)|，单位是分贝，相角的单位是度。由于增益用对数来表示（log(ab)=log(a)+log(b)），因此一传递函数乘以一常数，在伯德增益图只需将图形的纵向移动即可，二传递函数的相乘，在波德幅频图就变成图形的相加。幅频图纵轴0分贝以下具有正增益裕度、属稳定区，反之属不稳定区。

配合波德相频图可以估算一信号进入系统后，输出信号及原始信号的比例关系及相位。例如一个Asin(ωt) 的信号进入系统后振幅变原来的k倍，相位落后原信号Φ，则其输出信号则为(Ak)sin(ωt−Φ)，其中的k和Φ都是频率的函数。相频图纵轴-180度以上具有正相位裕度、属稳定区，反之属不稳定区。

2、伯德图的画法

画伯德图时，分三个频段进行，先画幅频特性，顺序是中频段、低频段和高频段。将三个频段的频率特性(或称频率响应)合起来就是全频段的幅频特性，然后再根据幅频特性画出相应的相频特性来。 作伯德图时，首先写出频率特性，然后按常数因子K、积分和微分因子(jω)、一阶因子(1+jωT)和二阶因子[1+2ζ(jω/ωn)+(jω)/ω]1这样四种基本因子分别画出伯德图，再总加而成。

下图是常见简易传递函数的伯德图趋势：

五、代码实现（C语言）

FFT.H

FFT.C

六、代码实现（Matlab）

基于MATLAB/Simulink的2ASK数字带通传输系统建模与仿真

相关文章

十分简明易懂的FFT（快速傅里叶变换）

彻底搞懂快速傅里叶变换FFT核心思想--分而治之

数字信号处理公式变程序（一）——DFT、FFT

实验笔记【3】| 利用matlab进行fft分析

信号处理之快速傅里叶变换(FFT)-通俗易懂

深入浅出的理解频谱泄露

快速傅里叶变换（FFT）和小波分析在信号处理上的应用