pytorch 交叉熵损失函数 BCELoss

BCE Loss

交叉熵损失函数计算公式：
BCE Loss = - 1/n*(y_actual * log(y_pred) + (1 - y_actual) * log(1 - y_pred))

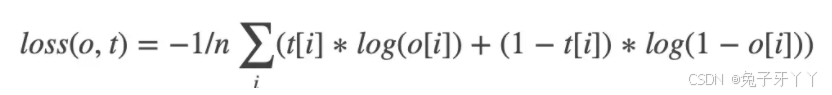
t[i]为标签值：0或者1

o[i]是经过sigmoid后的概率值

BCEWithLogitsLoss

这个损失将Sigmoid层和BCELoss合并在一个类中。

BCEWithLogitsLoss`(_weight=None_, _size_average=None_, _reduce=None_, _reduction='mean'_, _pos_weight=None_)

import torch
from torch import autograd
input = autograd.Variable(torch.tensor([[ 1.9072,  1.1079,  1.4906],[-0.6584, -0.0512,  0.7608],[-0.0614,  0.6583,  0.1095]]), requires_grad=True)
print(input)
print('-'*100)from torch import nn
m = nn.Sigmoid()
print(m(input))
print('-'*100)target = torch.FloatTensor([[0, 1, 1], [1, 1, 1], [0, 0, 0]])
print(target)
print('-'*100)import mathr11 = 0 * math.log(0.8707) + (1-0) * math.log((1 - 0.8707))
r12 = 1 * math.log(0.7517) + (1-1) * math.log((1 - 0.7517))
r13 = 1 * math.log(0.8162) + (1-1) * math.log((1 - 0.8162))r21 = 1 * math.log(0.3411) + (1-1) * math.log((1 - 0.3411))
r22 = 1 * math.log(0.4872) + (1-1) * math.log((1 - 0.4872))
r23 = 1 * math.log(0.6815) + (1-1) * math.log((1 - 0.6815))r31 = 0 * math.log(0.4847) + (1-0) * math.log((1 - 0.4847))
r32 = 0 * math.log(0.6589) + (1-0) * math.log((1 - 0.6589))
r33 = 0 * math.log(0.5273) + (1-0) * math.log((1 - 0.5273))r1 = -(r11 + r12 + r13) / 3
#0.8447112733378236
r2 = -(r21 + r22 + r23) / 3
#0.7260397266631787
r3 = -(r31 + r32 + r33) / 3
#0.8292933181294807
bceloss = (r1 + r2 + r3) / 3 
print(bceloss)
print('-'*100)loss = nn.BCELoss()
print(loss(m(input), target))
print('-'*100)loss = nn.BCEWithLogitsLoss()
print(loss(input, target))

结果

原始的3x3矩阵：

tensor([[ 1.9072,  1.1079,  1.4906],
        [-0.6584, -0.0512,  0.7608],
        [-0.0614,  0.6583,  0.1095]], requires_grad=True)
----------------------------------------------------------------------------------------------------

使用Sigmoid矩阵进行计算：

tensor([[0.8707, 0.7517, 0.8162],
        [0.3411, 0.4872, 0.6815],
        [0.4847, 0.6589, 0.5273]], grad_fn=<SigmoidBackward0>)
----------------------------------------------------------------------------------------------------

二分类标签：

tensor([[0., 1., 1.],
        [1., 1., 1.],
        [0., 0., 0.]])
----------------------------------------------------------------------------------------------------

手动计算的结果：

0.8000147727101611

----------------------------------------------------------------------------------------------------

使用BCE Loss对sigmoid后的计算的结果：

tensor(0.8000, grad_fn=<BinaryCrossEntropyBackward0>)
----------------------------------------------------------------------------------------------------

使用BCEWithLogitsLoss直接对原始数据计算的结果：

tensor(0.8000, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)