指派问题与匈牙利法讲解
指派问题概述:
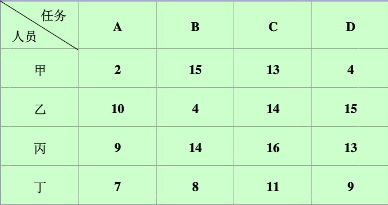
实际中,会遇到这样的问题,有n项不同的任务,需要n个人分别完成其中的1项,每个人完成任务的时间不一样。于是就有一个问题,如何分配任务使得花费时间最少。
通俗来讲,就是n*n矩阵中,选取n个元素,每行每列各有1个元素,使得和最小。
如下图:
指派问题性质:
指派问题的最优解有这样一个性质,若从矩阵的一行(列)各元素中分别减去该行(列)的最小元素,得到归约矩阵,其最优解和原矩阵的最优解相同.
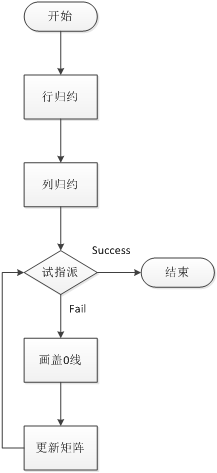
匈牙利法:
12 | 7 | 9 | 7 | 9 |
8 | 9 | 6 | 6 | 6 |
7 | 17 | 12 | 14 | 9 |
15 | 14 | 6 | 6 | 10 |
4 | 10 | 7 | 10 | 9 |
1.行归约:
每行元素减去该行的最小元素
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
2.列归约:
每列元素减去该列的最小元素
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
3.试指派:
(1)找到未被画线的含0元素最少的行列,即,遍历所有未被画线的0元素,看下该0元素所在的行列一共有多少个0,最终选取最少个数的那个0元素。
(2)找到该行列中未被画线的0元素,这就是一个独立0元素。对该0元素所在行和列画线。
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
(3)暂时不看被线覆盖的元素,重复(1)(2)直到没有线可以画。
(4)根据(2)找到的0元素个数判断,找到n个独立0元素则Success,小于n个则Fail.(本例子中,n=5,可以看到,第一次试指派之后,独立0元素有4个,不符合)
4.画盖0线:
目标:做最少的直线数覆盖所有0元素,直线数就是独立0元素的个数。
注意:这跟3的线不同;不能用贪心法去画线,比如
1 0 0
1 1 0
1 0 1
若先画横的,则得画3条线,实际只需2条;若先画竖的,将矩阵转置后同理。
步骤3得出的独立0元素的位置
5 | 0 | 2 | 0 | 2 |
2 | 3 | 0 | 0 | 0 |
0 | 10 | 5 | 7 | 2 |
9 | 8 | 0 | 0 | 4 |
0 | 6 | 3 | 6 | 5 |
(1)对没有独立0元素的行打勾、
(2)对打勾的行所含0元素的列打勾
(3)对所有打勾的列中所含独立0元素的行打勾
(4)重复(2)(3)直到没有不能再打勾
(5)对打勾的列和没有打勾的行画画线,这就是最小盖0线。
5 | 0 | 2 | 0 | 2 | |
2 | 3 | 0 | 0 | 0 | |
0 | 10 | 5 | 7 | 2 | √ |
9 | 8 | 0 | 0 | 4 | |
0 | 6 | 3 | 6 | 5 | √ |
√ |
5 | 0 | 2 | 0 | 2 | |
2 | 3 | 0 | 0 | 0 | |
0 | 10 | 5 | 7 | 2 | √ |
9 | 8 | 0 | 0 | 4 | |
0 | 6 | 3 | 6 | 5 | √ |
√ |
5.更新矩阵:
(1)对没有被线划到的数中,找到最小的数。
(2)对没有被线划到的数中,减去最小的数。
(3)对被2条线划到的数中,加上最小的数。
7 | 0 | 2 | 0 | 2 |
4 | 3 | 0 | 0 | 0 |
0 | 8 | 3 | 5 | 0 |
11 | 8 | 0 | 0 | 4 |
0 | 4 | 1 | 4 | 3 |
6.重复3-5直到成功。
0 | 1 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 0 | 0 | 1 |
0 | 0 | 0 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
sum = 7+6+9+6+4 = 32
匈牙利算法(Hungarian Algorithm)
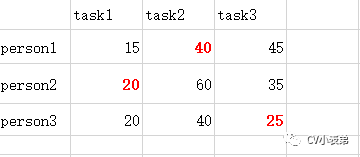
分配问题:假设有N个人N个任务,每个任务可以分配给任意不同的人,不同的人对不同的任务需要花费的代价也不相同,那么如何分配才能使花费总代价最少。假设现在有三个任务,三个人,每个人完成每个任务的代价矩阵如下(代价可以是时间或者金钱等):
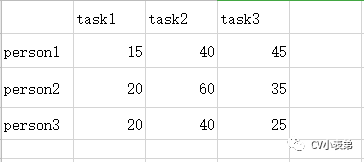
怎么才能找到一个分配方法使得任务花费代价最小呢?
匈牙利算法就是用来解决分配问题的一种方法,它基于理论:如果代价矩阵的某一行或某一列同时加或减某个数,则这个新的代价矩阵的最优分配任然是原代价矩阵的最优分配。
算法步骤(假设矩阵为NxN方阵):
1.对于矩阵的每一行,减去其中最小的元素
2.对于矩阵的每一列,减去其中最小的元素
3.用最少的水平线或垂直线覆盖矩阵中所有的0
4.如果线的数量等于N,则找到了最优分配,算法结束,否则进入步骤5
5.找到没有被任何线覆盖的最小元素,每个没被线覆盖的行减去这个元素,个被线覆盖的列加上这个元素,返回步骤3
继续拿上面的例子演示:
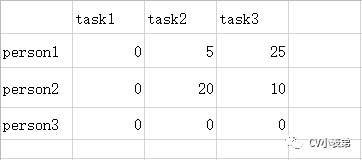
1.每一行减去其最小元素得到:

2.每一列减去其最小元素得到:
3.用最少的水平线或者垂直线覆盖所有的0得到:
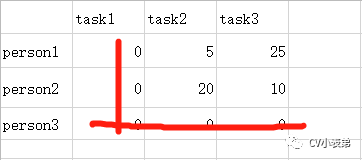
4.线的数量为2,小于3,进入第五步:
5.现在没被覆盖的最小元素是5,没被覆盖的行(第一和第二行)减去5,得到:

6.被覆盖的列(第一列)加上5,得到:
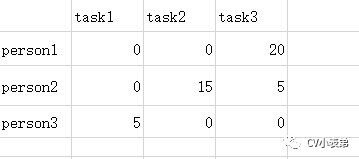
7.回到步骤3,用最少的线覆盖所有0:
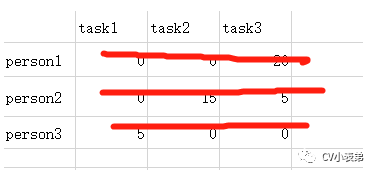
8.线的数量=3,算法结束,很显然,第一个任务给第二人,第二个任务给第一人,第三个任务给第三人,总代价最小(0+0+0):
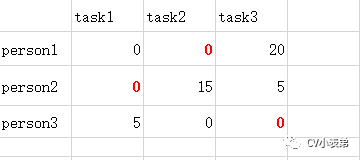
9.所以原矩阵最小代价为(40+20+25=85):
相关文章:

指派问题与匈牙利法讲解
指派问题概述:实际中,会遇到这样的问题,有n项不同的任务,需要n个人分别完成其中的1项,每个人完成任务的时间不一样。于是就有一个问题,如何分配任务使得花费时间最少。通俗来讲,就是n*n矩阵中&a…...
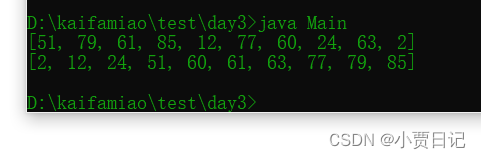
day5——冒泡排序,选择排序和插入排序的学习
选择排序冒泡排序插入排序 选择排序 选择排序的基本思路就是: 首先假定第一个的下表为所有元素中最小的一个, 然后用后面的每一个元素跟这个元素进行比较, 如果后面的元素比这个元素更小一点, 那么就将找到的最小的元素的下标和…...
)
Windows 数据类型 (Windows Data Types)
参考:https://learn.microsoft.com/en-us/windows/win32/winprog/windows-data-types 要求 要求值最低受支持的客户端Windows XP [仅限桌面应用]最低受支持的服务器Windows Server 2003 [仅限桌面应用]HeaderBaseTsd.h;WinDef.h;WinNT.hAPIENTRY 系统函数的调用约…...

九龙证券|本周5只新股申购,特斯拉、蔚来、理想的供应商来A股了!
据现在组织,2月13日到17日共有5只新股申购,其间上证主板2只,深证主板1只,北交所2只。 2月14日发动打新的深证主板新股多利科技成立于2010年,是一家专心于轿车冲压零部件及相关模具的开发、出产与出售的企业。从2020年…...
)
设计模式(持续更新)
本文主要是记录java的设计模式在实际工作中的应用案例,或者是对设计模式的个人理解及备忘 一、单例模式Singleton 工作场景(静态类): 在外部系统对接中,需要调用外部系统A的接口,但是接口是有身份校验的…...
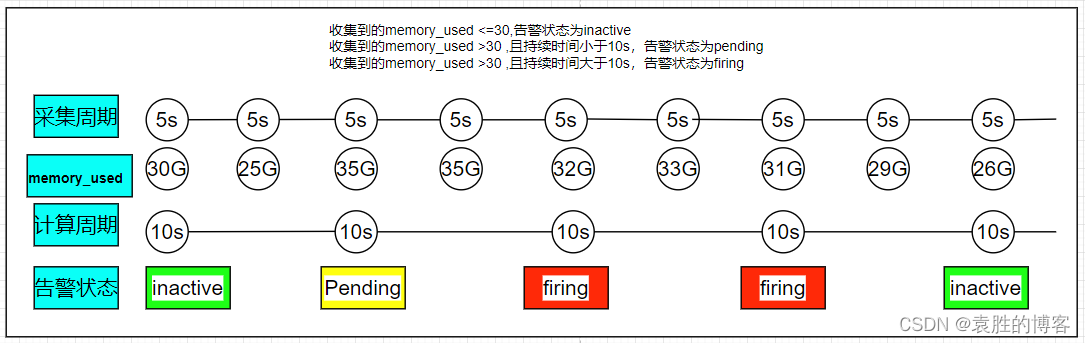
Prometheus 告警规则
Prometheus 告警规则 Prometheus官方内置的第三方报警通知包括:邮件、 即时通讯软件(如Slack、Hipchat)、移动应用消息推送(如Pushover)和自动化运维工具(例如:Pagerduty、Opsgenie、Victorops) Promethe…...

mulesoft MCIA 破釜沉舟备考 2023.02.13.02
mulesoft MCIA 破釜沉舟备考 2023.02.13.03 1. According to MuleSoft, which deployment charcateristic applies to a microservices application architecture?2. A mule application designed to fulfil two requirements3. A mule application must periodically process…...

获取DLL运行时路径的方法
之前项目中发现的问题,记录下解决方案1. 问题背景OVVRNTool项目中,底层图像基本操作功能由DLL库函数提供,上层基于DLL封装了两个应用CMD和GUI,然后通过Qt打包分发;发布是直接采用绿色免安装的方式打包,具体…...
)
“华为杯”研究生数学建模竞赛2006年-【华为杯】D题:学生面试中教师安排的优化与算法(附获奖论文)
赛题描述 高校自主招生是高考改革中的一项新生事物,现在仍处于探索阶段。某高校拟在全面衡量考生的高中学习成绩及综合表现后再采用专家面试的方式决定录取与否。该校在今年自主招生中,经过初选合格进入面试的考生有N人,拟聘请老师M人。每位学生要分别接受4位老师(简称该学…...
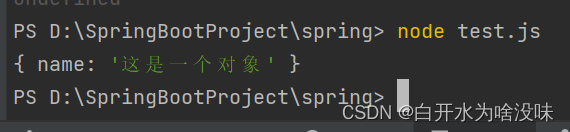
【JavaScript】复习 【对象参数】【函数参数】
js不会检查任何参数类型,任何参数都可以作为参数传递 1、对象参数 改变量随便改,改对象要看这个对象是不是有多个变量同时指向这个对象 const 用来定义常量,只能赋值一次。 变量------->对象------->属性 被const修饰的对象 …...
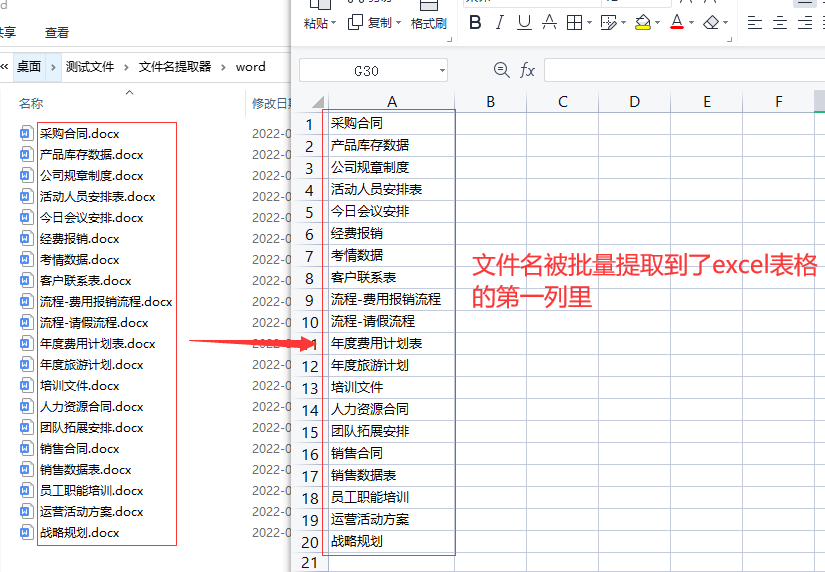
如何批量提取文件名到excel表格?
批量提取文件名到excel表格?关于这个问题相信很多人都遇到过,大多数人在第一次碰到的时候都不知道如何下手,大家都会立即在百度里面搜索相关方法教程,小编也试着搜索了一下,发现找到的很多方法都大同小异,需…...

CUDA线程层次一文搞懂|参加CUDA线上训练营
设备术语 Host:CPU 和 内存 (host memory)Device:GPU 和显存 (device memory) CUDA 线程层次 CUDA 线程层次分为: Thread 所有线程执行相同的核函数并行执行 Thread Block 执行在一个 Streaming Multiprocessor (SM)…...

Linux文件默认权限:umask
umask就是指定目前用户在建立文件或目录时候的权限默认值 查看方式有两种:一种可以直接输入umask,就可以看到数字类型的权限设置值,一种则是加入umask后加入-S(Symbolic)选项,就会以符号类型的方式来显示出…...

SonicWall:请立即修复SMA 1000 漏洞
近日,网络安全供应商SonicWall发布了关于安全移动访问 (SMA) 1000设备的三个安全漏洞的紧急报告,其中包括一个高威胁性的身份验证绕过漏洞。SonicWall指出,攻击者可以利用这些漏洞绕过授权,并可能破坏易受攻击的设备。 从报告中可…...

基于VS调试分析 + 堆栈观察问题代码段
文章目录问题代码段1 —— 阶乘之和问题代码段2 —— 越界的危害① 发现问题② 分析问题③ 思考问题【⭐堆栈原理⭐】④ 解决问题【DeBug与Release】👨程序员与测试人员👩✒总结与提炼问题代码段1 —— 阶乘之和 先来看一道C语言中比较基础的题目&#x…...
QFramework框架学习
主要学习内容TypeEventSystemActionKitTimer类1、TypeEventSystem-适用于一个条件触发,多个组件响应的情况例如:动物园系统中,点击肉食动物按钮,动物园中有肉食属性的动物都进行显示。步骤:1、动物自身脚本上进行判断是…...

移动OA系统,联动企业协作让办公高效无间断
移动oa系统,近年来随着企业办公节奏的变化及人们个性化办公需求的增加迎来了快速发展。一方面,它兼具OA系统诸多优势,既凝聚了企业基础管理工作,联动了企业协作、沟通交流,又进一步提高了企业的综合实力与市场竞争力。…...

结构体熟练掌握--实现通讯录
魔王的介绍:😶🌫️一名双非本科大一小白。魔王的目标:🤯努力赶上周围卷王的脚步。魔王的主页:🔥🔥🔥大魔王.🔥🔥🔥 ❤️…...

腾讯云CVM服务器购买流程手把手方法教程攻略
购买腾讯云服务器有两种方式。一种是在官方活动中,简单方便,但ECS配置相对固定;另一种是在ECS页面定制购买。配置选项丰富,但地理可用性区域、计费模式、CPU内存实例规格、映像系统、存储系统磁盘、网络带宽和安全组的选择更为复…...

九龙证券|“春季躁动”行情要来?1月新增投资者数大增
新增投资者数量在上一年12月触及多年新低后,2023年1月份开端呈现反弹。 在新增投资者数量之外,近段时刻以来,包含A股商场股票成交额、北向资金净买入额、两融资金规划及成交额在内多个商场目标也呈现回暖的特征,目前A股商场交投氛…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
