数据结构——基础知识补充
1.队列
1.普通队列
queue.Queue 是 Python 标准库 queue 模块中的一个类,适用于多线程环境。它实现了线程安全的 FIFO(先进先出)队列。
2.双端队列
双端队列(Deque,Double-Ended Queue)是一种具有队列和栈性质的数据结构,它允许我们在两端进行元素的添加(push)和移除(pop)操作。在Python中,双端队列可以通过collections模块中的deque类来实现。
deque是一个双端队列的实现,它提供了在两端快速添加和移除元素的能力。
当结合使用appendleft和popleft时,你实际上是在实现一个栈(Stack)的数据结构,因为栈是后进先出(LIFO)的,而这两个操作正好模拟了栈的“压栈”和“弹栈”行为。append和pop结合使用同理。
3.优先队列
优先队列(Priority Queue)是一种特殊的队列,其中的元素按照优先级进行排序。优先级最高的元素总是最先出队。Python 标准库中提供了 queue.PriorityQueue 和 heapq 模块来实现优先队列。
queue.PriorityQueue
queue.PriorityQueue 是 Python 标准库 queue 模块中的一个类,适用于多线程环境。它实现了线程安全的优先队列。
heapq
heapq 模块是 Python 标准库中的一个模块,提供了基于堆的优先队列实现。heapq 模块不是线程安全的,适用于单线程环境。
代码示例:
import queue
from collections import deque
import heapqdef pd_queue():"""# 普通队列 队尾入队 对头出队# put()入队# get() 出队q = queue.Queue()q.put(55)q.put(44)q.put(33)print(q.qsize())print(q.get())print(q.get())print(q.get())"""# deque 双端队列 既可以在队尾进行入队和出队操作# 也可以在队头进行入队和出队操作# append()在队尾入队# appendleft()在队头入队# pop()在队尾出队# popleft()在队头出队# appendleft()和popleft()组合使用时 相当于栈的操作# append()和pop()同理dq = deque()dq.append(10)dq.append(20)dq.appendleft(30)dq.appendleft(40)print(dq.popleft())print(dq.popleft())print(dq.popleft())print(dq.popleft())print("----------------------------------------")pq = queue.PriorityQueue()pq.put((2,"item2"))pq.put((1,"item1"))pq.put((4,"item4"))pq.put((3,"item3"))print(pq.get())print(pq.get())print(pq.get())print(pq.get())print("----------------------------------------")# headq 优先队列 基于堆实现的 要预先定义一个数组作为heap堆对象 线程不安全# heappush() 向队中添加元素元组(优先级 元素值) 优先级的数值越小heap = []heapq.heappush(heap, (1,"hq1"))heapq.heappush(heap, (3,"hq3"))heapq.heappush(heap, (2,"hq2"))heapq.heappush(heap, (4,"hq4"))print(heapq.heappop(heap))print(heapq.heappop(heap))print(heapq.heappop(heap))print(heapq.heappop(heap))
if __name__ == '__main__':pd_queue()2.树
1.概念
1.术语
在描述树的各个部分的时候有很多术语。
-
为了让介绍的内容更容易理解, 需要知道一些树的术语.
-
不过大部分术语都与真实世界的树相关, 或者和家庭关系相关(如父节点和子节点), 所以它们比较容易理解.
我们先来看一下树的结构

2.树的定义
-
树(Tree): n(n≥0)个结点构成的有限集合。
-
当n=0时,称为空树;
-
对于任一棵非空树(n> 0),它具备以下性质:
-
树中有一个称为“根(Root)”的特殊结点,用 root 表示;
-
其余结点可分为m(m>0)个互不相交的有限集T1,T2,... ,Tm,其中每个集合本身又是一棵树,称为原来树的“子树(SubTree)”
注意:
-
子树之间不可以相交
-
除了根结点外,每个结点有且仅有一个父结点;
-
一棵N个结点的树有N-1条边。
-
3.树的术语:
-
1.结点的度(Degree):结点的子树个数.
-
2.树的度:树的所有结点中最大的度数. (树的度通常为结点的个数N-1)
-
3.叶子结点(Leaf):度为0的结点. (也称为叶子结点)
-
4.父结点(Parent):有子树的结点是其子树的根结点的父结点
-
5.子结点(Child):若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子结点。
-
6.兄弟结点(Sibling):具有同一父结点的各结点彼此是兄弟结点。
-
7.路径和路径长度:从结点n1到nk的路径为一个结点序列n1 , n2,… , nk, ni是 ni+1的父结点。路径所包含边的个数为路径的长度。
-
8.结点的层次(Level):规定根结点在1层,其它任一结点的层数是其父结点的层数加1。
-
9.树的深度(Depth):树中所有结点中的最大层次是这棵树的深度。
2.二叉树
1.概念
二叉树的定义
- 二叉树可以为空, 也就是没有结点.
- 若不为空,则它是由根结点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。
二叉树有五种形态:
- 注意c和d是不同的二叉树, 因为二叉树是有左右之分的.

2.特性
二叉树有几个比较重要的特性, 在笔试题中比较常见:
- 一个二叉树第 i 层的最大结点数为:2^(i-1), i >= 1;
- 深度为k的二叉树有最大结点总数为: 2^k - 1, k >= 1;
- 对任何非空二叉树 T,若n0表示叶结点的个数、n2是度为2的非叶结点个数,那么两者满足关系n0 = n2 + 1。

3.特殊的二叉树
1.满二叉树(Full Binary Tree)
在二叉树中, 除了最下一层的叶结点外, 每层节点都有2个子结点, 就构成了满二叉树.

2.完全二叉树(Complete Binary Tree)
- 除二叉树最后一层外, 其他各层的节点数都达到最大个数.
- 且最后一层从左向右的叶结点连续存在, 只缺右侧若干节点.
- 满二叉树是特殊的完全二叉树.
- 下面不是完全二叉树, 因为D节点还没有右结点, 但是E节点就有了左右节点.
 4.二叉树的存储
4.二叉树的存储
二叉树的存储常见的方式是链表.
链表存储:
- 二叉树最常见的方式还是使用链表存储.
- 每个结点封装成一个Node, Node中包含存储的数据, 左结点的引用, 右结点的引用.

5.二叉树遍历
前序遍历(Pre-order Traversal)、中序遍历(In-order Traversal)和后序遍历(Post-order Traversal)是二叉树的三种基本遍历方式。
遍历规则:
- 前序遍历,按照以下顺序访问节点:根节点、左子树、右子树。
- 中序遍历,按照以下顺序访问节点:左子树、根节点、右子树。
- 后序遍历,按照以下顺序访问节点:左子树、右子树、根节点。
3.二叉查找树
二叉查找树(Binary Search Tree, BST)是一种特殊的二叉树,它具有以下性质:
- 每个节点都有一个键值(key)。
- 对于每个节点,其左子树中的所有节点的键值都小于该节点的键值。
- 对于每个节点,其右子树中的所有节点的键值都大于该节点的键值。
- 左子树和右子树也分别是二叉查找树。
- 二叉查找树不允许出现键值相等的结点。
二叉查找树的主要操作包括插入、删除和遍历。
1.创建二叉查找树
class TreeNode:def __init__(self, key):self.key = keyself.left = Noneself.right = None参数说明:
-
key: 节点的键值。
-
left: 指向左子节点的指针。
-
right: 指向右子节点的指针。
2.创建二叉查找树
class BinarySearchTree:def __init__(self):self.root = None-
root: 指向二叉搜索树的根节点。初始时为 None。
3.插入节点
插入操作的步骤:
-
如果树为空:直接将新节点作为根节点。
-
如果树不为空:
-
从根节点开始,根据新节点的键值与当前节点的键值的比较结果,决定向左子树还是右子树移动。
-
如果新节点的键值小于当前节点的键值,如果当前节点没有左子树,则将新节点插入到当前节点的左子树,否则向左子树移动。
-
如果新节点的键值大于当前节点的键值,如果当前节点没有右子树,则将新节点插入到当前节点的右子树,否则向右子树移动。
-
重复上述步骤,直到找到一个空位置,将新节点插入到该位置。
-
def insert(self, key):if self.root is None:self.root = TreeNode(key)else:self._insert(self.root, key)def _insert(self, node, key):if key < node.key:if node.left is None:node.left = TreeNode(key)else:self._insert(node.left, key)elif key > node.key:if node.right is None:node.right = TreeNode(key)else:self._insert(node.right, key)-
insert(key): 公开的插入方法。如果树为空,则创建一个新节点作为根节点;否则,调用 _insert 方法进行递归插入。
-
_insert(node, key): 递归插入方法。根据键值的大小,递归地在左子树或右子树中插入新节点。
4.查找节点
def search(self, key):return self._search(self.root, key)def _search(self, node, key):if node is None or node.key == key:return nodeif key < node.key:return self._search(node.left, key)return self._search(node.right, key)5.删除节点
删除逻辑:
1.递归查找待删除节点
-
如果待删除节点的键值小于当前节点的键值,递归地在左子树中查找并删除。
-
如果待删除节点的键值大于当前节点的键值,递归地在右子树中查找并删除。
2.找到待删除节点
删除操作的步骤可以分为以下几种情况:
-
待删除节点是叶子节点(没有子节点):直接删除该节点。
-
待删除节点只有一个子节点:用其子节点替换该节点。
-
待删除节点有两个子节点:
-
找到右子树中的最小节点(即后继节点)。
-
用后继节点的键值替换待删除节点的键值。
-
删除后继节点(后继节点要么是叶子节点,要么只有一个右子节点)。
-
def _remove(self, node, key):# 如果树为空则返回Noneif node is None:return None# 判断指定的key和当前节点的key的大小 如果指定的key小于当前节点的key 则递归遍历左子树# 如果指定的key大于当前节点的key 则递归遍历右子树if key < node.key:node.left = self._remove(node.left, key)elif key > node.key:node.right = self._remove(node.right, key)# 如果指定key等于当前节点key# 1.当前节点没有子节点 直接删除 返回None# 2.当前节点有一个子节点# 1.有右子节点 用右子节点替换当前节点# 2.有左子节点 用左子节点替换当前节点# 3.当前节点有两个节点# 查找当前节点的右节点的最小值 找到最小值 用这个最小值来替代当前节点else:# 如果当前节点 左右子树都为空 则返回Noneif node.left is None and node.right is None:return None# 如果左子树为空 则返回右子树elif node.left is None:return node.right# 如果右子树为空 则返回左子树elif node.right is None:return node.left# 如果当前节点右两个子树 则查询当前节点右子树的左子树找到最小值节点# 将最小值替换到当前节点 将最小值节点递归删除else:temp = self._min_value_node(node.right)node.key = temp.key# 以当前节点的右子树节点为根节点 删除最小值节点node.right = self._remove(node.right,temp.key)return node# 查找当前节点的最小值 最小值在当前节点的左子树中def _min_value_node(self,node):current = nodewhile current.left is not None:current = current.leftreturn node
6.遍历
遍历规则:
前序遍历,按照以下顺序访问节点:根节点、左子树、右子树。
中序遍历,按照以下顺序访问节点:左子树、根节点、右子树。
后序遍历,按照以下顺序访问节点:左子树、右子树、根节点。
# 中序遍历def inorder_search(self):result = []self._inorder_search(self.root,result)return resultdef _inorder_search(self,node,result):if node:self._inorder_search(node.left,result)result.append(node.key)self._inorder_search(node.right,result)# 前序遍历def preorder_search(self):result = []if self.root is None:return Noneself._preorder_search(self.root,result)return resultdef _preorder_search(self,node,result):if node:result.append(node.key)self._preorder_search(node.left, result)self._preorder_search(node.right, result)# 后序遍历def afterorder_search(self):result = []self._afterorder_search(self.root, result)return resultdef _afterorder_search(self, node, result):if node:self._afterorder_search(node.left, result)self._afterorder_search(node.right, result)result.append(node.key)
整个代码实现:
# 定义二叉查找树节点
class TreeNode:def __init__(self, key):self.key = keyself.left = Noneself.right = Noneclass BST:def __init__(self,):self.root = Nonedef insert(self, key):# 判断根节点是否为空 为空则将值赋给根节点if self.root is None:self.root = TreeNode(key)else:self._insert(self.root,key)def _insert(self, node, key):# 如果要插入的键值小于当前节点的键值# 则判断当前节点是否有左子树 没有则将新节点赋给当前节点的左子树# 有则继续向当前节点的左子树移动 递归插入if key < node.key:if node.left is None:node.left = TreeNode(key)else:# node.left表示当前节点的左子树节点self._insert(node.left,key)# 如果要插入的键值大于当前节点的键值# 则判断当前节点是否有右子树 没有则将新节点赋给当前节点的右子树# 有则继续向当前节点的右子树移动 递归插入else :if node.right is None:node.right = TreeNode(key)else:self._insert(node.right, key)# 中序遍历def inorder_search(self):result = []self._inorder_search(self.root,result)return resultdef _inorder_search(self,node,result):if node:self._inorder_search(node.left,result)result.append(node.key)self._inorder_search(node.right,result)# 前序遍历def preorder_search(self):result = []if self.root is None:return Noneself._preorder_search(self.root,result)return resultdef _preorder_search(self,node,result):if node:result.append(node.key)self._preorder_search(node.left, result)self._preorder_search(node.right, result)# 后序遍历def afterorder_search(self):result = []self._afterorder_search(self.root, result)return resultdef _afterorder_search(self, node, result):if node:self._afterorder_search(node.left, result)self._afterorder_search(node.right, result)result.append(node.key)def remove_bst(self, key):self.root = self._remove(self.root, key)def _remove(self, node, key):# 如果树为空则返回Noneif node is None:return None# 判断指定的key和当前节点的key的大小 如果指定的key小于当前节点的key 则递归遍历左子树# 如果指定的key大于当前节点的key 则递归遍历右子树if key < node.key:node.left = self._remove(node.left, key)elif key > node.key:node.right = self._remove(node.right, key)# 如果指定key等于当前节点key# 1.当前节点没有子节点 直接删除 返回None# 2.当前节点有一个子节点# 1.有右子节点 用右子节点替换当前节点# 2.有左子节点 用左子节点替换当前节点# 3.当前节点有两个节点# 查找当前节点的右节点的最小值 找到最小值 用这个最小值来替代当前节点else:# 如果当前节点 左右子树都为空 则返回Noneif node.left is None and node.right is None:return None# 如果左子树为空 则返回右子树elif node.left is None:return node.right# 如果右子树为空 则返回左子树elif node.right is None:return node.left# 如果当前节点右两个子树 则查询当前节点右子树的左子树找到最小值节点# 将最小值替换到当前节点 将最小值节点递归删除else:temp = self._min_value_node(node.right)node.key = temp.key# 以当前节点的右子树节点为根节点 删除最小值节点node.right = self._remove(node.right,temp.key)return node# 查找当前节点的最小值 最小值在当前节点的左子树中def _min_value_node(self,node):current = nodewhile current.left is not None:current = current.leftreturn nodeif __name__ == '__main__':bst = BST()bst.insert(3)bst.insert(1)bst.insert(2)bst.insert(5)bst.insert(4)# result = bst.inorder_search()# result = bst.preorder_search()result = bst.afterorder_search()print(result)
相关文章:

数据结构——基础知识补充
1.队列 1.普通队列 queue.Queue 是 Python 标准库 queue 模块中的一个类,适用于多线程环境。它实现了线程安全的 FIFO(先进先出)队列。 2.双端队列 双端队列(Deque,Double-Ended Queue)是一种具有队列和…...

只有.git文件夹时如何恢复项目
有时候误删文件但由于.git是隐藏文件夹而幸存,或者项目太大,单单甩给你一个.git文件夹让你自己恢复整个项目,该怎么办呢? 不用担心,只要进行以下步骤,即可把原项目重新搭建起来: 创建一个文件…...

anchor、anchor box、bounding box之间关系
最近学YOLO接触到这些概念,一下子有点蒙,简单总结一下。 anchor和anchor box Anchor:表示一组预定义的尺寸比例,用来代表常见物体的宽高比。可以把它看成是一个模板或规格,定义了物体框的“形状”和“比例”ÿ…...

代码随想录算法训练营第三十天 | 452.用最少数量的箭引爆气球 435.无重叠区间 763.划分字母区间
LeetCode 452.用最少数量的箭引爆气球: 文章链接 题目链接:452.用最少数量的箭引爆气球 思路: 气球的区间有重叠部分,只要弓箭从重叠部分射出来,那么就能减少所使用的弓箭数 **局部最优:**只要有重叠部分…...

海亮科技亮相第84届中国教装展 尽显生于校园 长于校园教育基因
10月25日,第84届中国教育装备展示会(以下简称“教装展”)在昆明滇池国际会展中心开幕。作为国内教育装备领域规模最大、影响最广的专业展会,本届教装展以“数字赋能教育,创新引领未来”为主题,为教育领域新…...

C语言数据结构学习:栈
C语言 数据结构学习 汇总入口: C语言数据结构学习:[汇总] 1. 栈 栈,实际上是一种特殊的线性表。这里使用的是链表栈,链表栈的博客:C语言数据结构学习:单链表 2. 栈的特点 只能在一端进行存取操作&#x…...

如何快速分析音频中的各种频率成分
从视频中提取音频 from moviepy.editor import VideoFileClip# Load the video file and extract audio video_path "/mnt/data/WeChat_20241026235630.mp4" video_clip VideoFileClip(video_path)# Extract audio and save as a temporary file for further anal…...

MongoDB 6.0 主从复制配置
以下是 MongoDB 6.0 版本配置主从的详细安装步骤: 1. 安装 MongoDB:可以从官网下载 MongoDB 6.0 的安装包并进行安装,或者使用相应的包管理工具进行安装。 2. 配置主节点:在主节点的 MongoDB 配置文件(默认路径为 …...

NPU 神经网络处理单元
Ⅰ 什么是 NPU? 当前正处于神经网络和机器学习处理需求爆发的初期。传统的 CPU(中央处理器)/GPU(图形处理器)可以执行类似任务,但专门为神经网络优化的 NPU(神经处理单元)比 CPU/GP…...

安宝特分享 | AR技术引领:跨国工业远程协作创新模式
在当今高度互联的工业环境中,跨国合作与沟通变得日益重要。然而,语言障碍常常成为高效协作的绊脚石。安宝特AR眼镜凭借其强大的多语言自动翻译和播报功能,正在改变这一局面,让远程协作变得更加顺畅。 01 多语言翻译优势 安宝特A…...
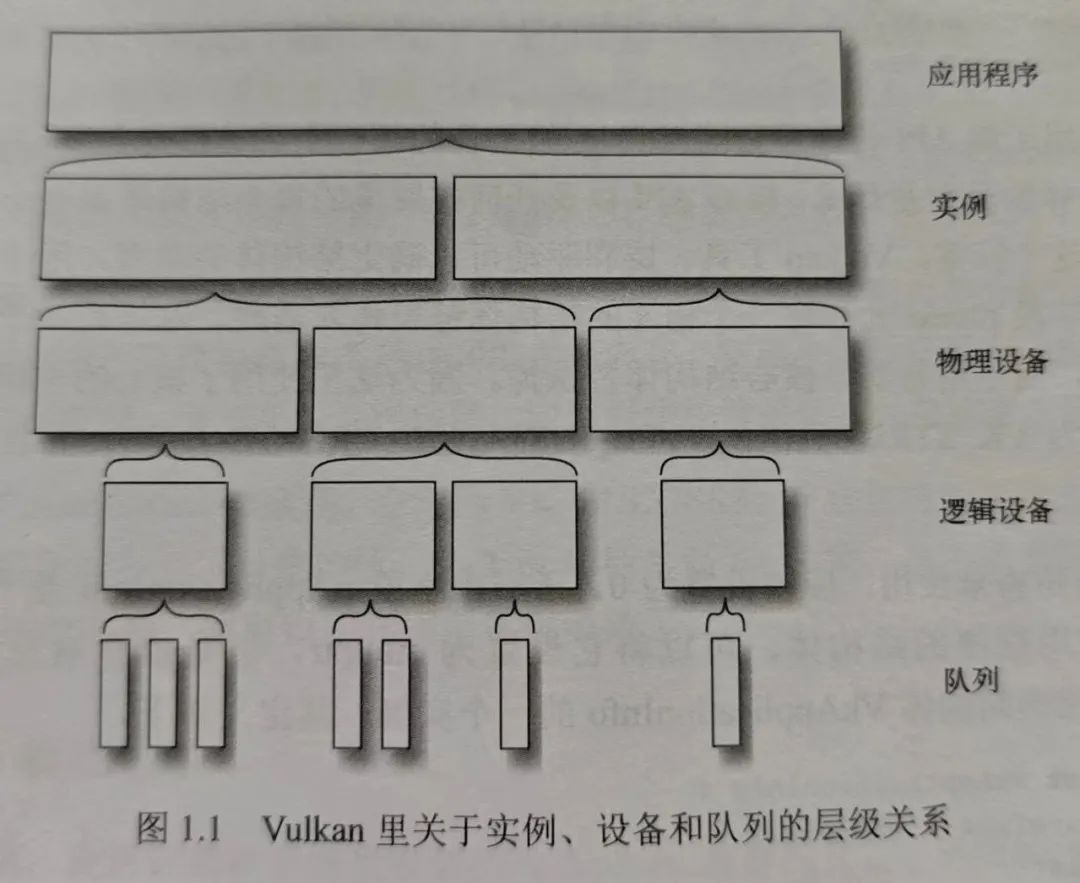
Vulkan 开发(五):Vulkan 逻辑设备
图片来自《Vulkan 应用开发指南》 Vulkan 开发系列文章: 1. 开篇,Vulkan 概述 2. Vulkan 实例 3. Vulkan 物理设备 4. Vulkan 设备队列 在 Vulkan 中,逻辑设备(Logical Device)是与物理设备(Physical D…...

Kafka 解决消息丢失、乱序与重复消费
一、引言 在分布式系统中,Apache Kafka 作为一种高吞吐量的分布式发布订阅消息系统,被广泛应用于日志收集、流式处理、消息队列等场景。然而,在实际使用过程中,可能会遇到消息丢失、乱序、重复消费等问题,这些问题可能…...

计算机专业毕业生面试工具推荐:白瓜面试
随着毕业季的临近,计算机专业的毕业生们即将步入职场,面试成为了他们必须面对的挑战。在这个过程中,选择合适的面试工具可以大大提高求职成功率。今天,我要向大家推荐一款专为计算机专业毕业生设计的面试工具——白瓜面试。 为什…...

数字IC开发:布局布线
数字IC开发:布局布线 前端经过DFT,综合后输出网表文件给后端,由后端通过布局布线,将网表转换为GDSII文件;网表文件只包含单元器件及其连接等信息,GDS文件则包含其物理位置,具体的走线࿱…...

高空作业未系安全带监测系统 安全带穿戴识别预警系统
在各类高空作业场景中,安全带是保障作业人员生命安全的关键防线。然而,由于人为疏忽或其他原因,作业人员未正确系挂安全带的情况时有发生,这给高空作业带来了巨大的安全隐患。为有效解决这一问题,高空作业未系安全带监…...

k8s的配置和存储(ConfigMap、Secret、Hostpath、EmptyDir以及NFS的服务使用)
ConfigMap 简介 在 Kubernetes 中,ConfigMap 是一种用于存储非敏感信息的 Kubernetes 对象。它用于存储配置数据,如键值对、整个配置文件或 JSON 数据等。ConfigMap 通常用于容器镜像中的配置文件、命令行参数和环境变量等。 ConfigMap 可以通过三种方…...

JS轮播图实现自动轮播、悬浮停止轮播、点击切换,下方指示器与图片联动效果
代码: <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><s…...
使用 Kafka 和 MinIO 实现人工智能数据工作流
MinIO Enterprise Object Store 是用于创建和执行复杂数据工作流的基础组件。此事件驱动功能的核心是使用 Kafka 的 MinIO 存储桶通知。MinIO Enterprise Object Store 为所有 HTTP 请求(如 PUT、POST、COPY、DELETE、GET、HEAD 和 CompleteMultipartUpload…...

力扣题86~90
题86(中等): python代码 # Definition for singly-linked list. # class ListNode: # def __init__(self, val0, nextNone): # self.val val # self.next next class Solution:def partition(self, head: Optional[Li…...

【JavaEE】【多线程】定时器
目录 一、定时器简介1.1 Timer类1.2 使用案例 二、实现简易定时器2.1 MyTimerTask类2.2 实现schedule方法2.3 构造方法2.4 总代码2.5 测试 一、定时器简介 定时器:就相当于一个闹钟,当我们定的时间到了,那么就执行一些逻辑。 1.1 Timer类 …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
