「二叉树进阶题解:构建、遍历与结构转化全解析」

文章目录
- 根据二叉树创建字符串
- 思路
- 代码
- 二叉树的层序遍历
- 思路
- 代码
- 二叉树的最近公共祖先
- 思路
- 代码
- 二叉搜索树与双向链表
- 思路
- 代码
- 从前序与中序遍历序列构造二叉树
- 思路
- 代码
- 总结
根据二叉树创建字符串
题目:

样例:


可以看见,唯一特殊的就是左子树,当右子树存在的时候左子树不存在的时候,我们需要用()代表空,但是没有左子树,又没有右子树的时候,我们不需要做任何处理。
思路
结合题目和样例,我们可以知道,特殊的是右子树存在但是左子树不存在的情况,这种情况,可以归类为root->left||root->right。这种情况,我们就要处理左子树。首先我们应该处理一下需要返回的字符串,

- 有左子树的情况,当有左子树的时候,我们直接递归左子树,并将结果加上()
- 没有左子树,但是有有右子树,也需要递归一次左子树,因为需要加上空的()
- 有右子树,直接递归右子树,最后在结果上加上()。
代码
class Solution {
public:string tree2str(TreeNode* root) {if(root==nullptr) return "";string result=to_string(root->val);if(root->left||root->right){result+="("+tree2str(root->left)+")";}if(root->right){result+="("+tree2str(root->right)+")";}return result;}
};
二叉树的层序遍历
题目:

样例:

思路
这道题可以直接借助队列,借助队列的时候我们还需要一个levelsize来记录每层的个数即可
代码
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if(root==nullptr)return vector<vector<int>>();//创建队列queue<TreeNode*> q;q.push(root);vector<vector<int>> result;int levelsize=1;while(!q.empty()){vector<int> level;for(int i=0;i<levelsize;i++){auto front=q.front();q.pop();if(front->left)q.push(front->left);if(front->right)q.push(front->right);level.push_back(front->val);}result.push_back(level);levelsize=q.size();}return result;}
};
二叉树的最近公共祖先
题目:

样例:

思路
需要找公共祖先,首先我们肯定要找到这两个节点的位置,然后这两个节点向上返回,我们用left表示是向左子树搜索这个节点,用right表示向右子树搜索这两个节点,如果能找到就返回对应的节点,p或者q,如果没找到就返回nullptr,如果left和right都不为空说明p和q分布在左子树和右子树,并且root就是两个的最近的祖先,如果其中一个是nullptr说明,p和q分布在一边,直接返回不为空的那个就是最近公共祖先。
代码
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//找对应的节点if(root==nullptr||root==p||root==q)return root;//记录左子树的结果TreeNode* left=lowestCommonAncestor(root->left,p,q);//记录右子树的结果TreeNode* right=lowestCommonAncestor(root->right,p,q);//如果左右子树都不为空则说明和q分布在左子树和右子树if(left&&right)return root;//如果其中一个是空,则说明p是祖先或者q是祖先return (left==nullptr)?right:left;}
};
二叉搜索树与双向链表
题目:

样例:

思路
首先我们来看看子问题:
这肯定是一个中序遍历吧,因为只有中序遍历才能是顺序的,这很明显,接下来就是我们需要处理的中序中间的部分,就是节点之间关系的转变。

从这里可以知道左指针是指向前驱的指针,右指针是指向后继的指针。

这里我们分别对左子树和右子树进行中序遍历,第一个遍历到4,因为4是第一个,所以前驱应该是nullptr,因为每次我们都需要前驱,所以这里我们用parent表示前驱,parent就应该被初始化为nullptr,当中序遍历到达4的时候4是不需要处理的因为4的左子树和右子树都是nullptr,唯一需要处理的就是4的前驱应该是nullptr,处理完之后,我们需要返回前驱,因为6需要指向前驱,前驱不为空的情况下还需要将前驱的右指针指向后继,4的后继是6,所以我们只需要进行两个步骤,第一个步骤是处理前驱,前驱是已知节点指向前驱节点,所以我们不用担心是否为空,因为我们的前驱parent初始化是nullptr,所以在parent指向后继的时候,需要判断一下parent是否是空。
最后再改变前驱即可左子树的前驱就是最后一个访问的节点,左中右,所以上图应该是8。
代码
class Solution {
public:TreeNode* parent=nullptr;void InOrder(TreeNode* root){//root是nullptr返回if(!root)return;//中序遍历InOrder(root->left);//先将root的前驱指针指向parent,root赋值给parentroot->left = parent;if(parent) parent->right=root;parent = root;InOrder(root->right);}//左指针指向前面,右指针指向后面TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree==nullptr)return nullptr;TreeNode* first=pRootOfTree;while(first->left) first=first->left;InOrder(pRootOfTree);return first;}
};
从前序与中序遍历序列构造二叉树
题目:

样例:

思路
首先已知两个序列:

前序和中序,根据前序的特性我们可以知道,第一个元素肯定是根节点,所以这里我们可以根据前序遍历找到根节点,然后在中序遍历中找到根节点的位置。

找到在中序中的位置之后我们可以通过中序的特性,左边是左子树,右边是右子树,来对左区间和右区间递归,根节点的left指向左区间,根节点的right指向右区间,然后循环这个过程。
代码
class Solution {
public://构建二叉树TreeNode* Build(vector<int>& preorder,int preL,int preR,vector<int> inorder,int inL,int inR){//当左边大于右边的时候返回nullptrif(preL>preR)return nullptr;//找出根节点的值int rootval=preorder[preL];TreeNode *root=new TreeNode(rootval);//找到在中序遍历中的位置int index=inL;while(inorder[index]!=rootval) index++;//计算左子树在前序中的位置int leftSize=index-inL;root->left=Build(preorder,preL+1,preL+leftSize,inorder,inL,index-1);root->right=Build(preorder,preL+leftSize+1,preR,inorder,index+1,inR);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {return Build(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1);}
};
总结
通过多道二叉树题目的练习,我们全面了解了二叉树的各种操作和特性。每道题目都涉及不同的场景和技巧,如节点删除、树的遍历、以及特殊结构转换等,不仅加深了对二叉树结构的理解,也提升了编写递归和迭代算法的能力。这些经验为进一步深入数据结构和算法的学习打下了扎实的基础。希望这篇总结能够帮助你在二叉树题目中更得心应手,为更复杂的数据结构问题做好准备。
相关文章:

「二叉树进阶题解:构建、遍历与结构转化全解析」
文章目录 根据二叉树创建字符串思路代码 二叉树的层序遍历思路代码 二叉树的最近公共祖先思路代码 二叉搜索树与双向链表思路代码 从前序与中序遍历序列构造二叉树思路代码 总结 根据二叉树创建字符串 题目: 样例: 可以看见,唯一特殊的就…...

在使用代理IP时,需要注意以下几点:
1. 代理IP的质量和稳定性直接影响爬虫的效果。因此,我们需要定期更新代理IP列表,并筛选出可用的代理IP。 2. 有些代理IP可能存在被目标网站封禁的风险。因此,我们需要合理使用代理IP,避免过度频繁地访问目标网站。 3. 在使用代…...

深入理解Java基础概念的高级应用(1/5)
目录 1. Java内存模型:堆、栈与方法区 示例代码:对象存储位置 2. 类加载器的工作原理 示例代码:自定义类加载器 3. JVM如何执行字节码 字节码指令示例 4. Java基础数据类型的存储与操作 自动装箱与拆箱 示例代码:基础类型…...

高可用HA软件
高可用HA(High Availability)软件在分布式系统架构设计中至关重要,它们能够减少系统停机时间,确保应用程序持久、不间断地提供服务。以下是四款常用的高可用HA软件介绍: Keepalived Keepalived起初是为LVS(…...

《近似线性可分支持向量机的原理推导》 拉格朗日函数 公式解析
本文是将文章《近似线性可分支持向量机的原理推导》中的公式单独拿出来做一个详细的解析,便于初学者更好的理解。 公式 9-41 解释: L ( w , b , ξ , α , μ ) 1 2 ∥ w ∥ 2 C ∑ i 1 N ξ i − ∑ i 1 N α i ( y i ( w T x i b ) − ( 1 − ξ …...

9.指针和字符串string类型
指针和字符串string类型 1.指针2.字符串string类型 1.指针 C完全兼容C语言指针,C多出一个this指针 交换两数 #include <iostream>using namespace std;void swap(int *a,int *b){int temp;temp *a;*a *b;*b temp; }int main() {//交换前int a 50;int b …...

八,Linux基础环境搭建(CentOS7)- 安装Mysql和Hive
Linux基础环境搭建(CentOS7)- 安装Mysql和Hive 大家注意以下的环境搭建版本号,如果版本不匹配有可能出现问题! 一、Mysql下载及安装 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB 公司开发,属于 Orac…...

海量数据面试题
⭐️前言⭐️ 本篇文章主要针对在面试时可能涉及到的海量数据的面试题,该类型面试题常常考虑通过位图、布隆过滤器或者哈希的方式来解决。 🍉欢迎点赞 👍 收藏 ⭐留言评论 🍉博主将持续更新学习记录收获,友友们有任何…...

基于SSM积分商城管理系统的设计与实现(源码+lw+部署文档+讲解等)
前言 伴随着基础网络设施的不断进步和终端电子设备的高度普及,互联网用户规模越来越大。现在人们越来越离不开计算机网络、互联网所带来的好处了,现如今不同的网站系统遍地都是,现在已经不同于以往的传统的管理方式了,只有跟上时代…...

MLP预售开启,革新去中心化通信生态:智能手机与AI Agent齐上阵
2024年10月22日,Matrix Layer Protocol(MLP)宣布其备受期待的第一期产品正式进入预售阶段。随着Web3世界的不断发展,去中心化技术已经深入到我们日常生活的方方面面。作为Web3世界中炙手可热的创新项目,Matrix Layer P…...

js获取浏览器指纹
Canvas指纹法 来源:https://www.cnblogs.com/leijing0607/p/8044218.html 从根本上来说,每一种浏览器都会使用不同的图像处理引擎,不同的导出选项,不同的压缩等级,所以每一台电脑绘制出的图形都会有些许不同…...

乐尚代驾的项目问题
订单状态如果在流转的过程中卡住了,怎么办? 卡住的原因有可能是: 网络问题 网络不稳定或中断可能导致订单状态更新的请求无法及时发送或接收。例如,司机端在更新代驾车辆信息时,如果网络出现故障,可能无法…...

uniapp app.onshow 和 onMounted一样用吗
在uni-app中,onShow和onMounted并不完全相同,它们分别属于应用生命周期和组件生命周期。 应用生命周期中的onShow 在uni-app中,onShow是应用生命周期的一部分,它会在应用启动或从后台进入前台时触发。这意味着它不仅仅局限于页…...

基于Mysql、JavaScript、PHP、ajax开发的MBTI性格测试网站(前端+后端)
源码地址:https://download.csdn.net/download/2302_79553009/89933699 项目简介 本项目旨在构建一个基于MBTI(迈尔斯-布里格斯性格分类指标)理论的在线平台——“16Personalities”。该平台利用PHP、MySQL、JavaScript等技术栈开发…...

【问题解决】连接mysql时报错caching_sha2_password can not load
一, 问题 在连接Mysql时报错, caching_sha2_password can not load 二,问题原因 报错信息 "caching_sha2_password can not load" 通常出现在尝试连接到使用 MySQL 8.0 或更高版本的数据库时,因为从 MySQL 8.0 开始&a…...

【瑞吉外卖】-day01
目录 前言 第一天项目启动 获取资料 创建项目 编辑 连接本地数据库 连接数据库 修改用户名和密码 编辑创建表 创建启动类来进行测试 导入前端页面 创建项目所需目录 检查登录功能 登录界面 登录成功 登录失败 代码 退出功能 易错点 前言 尝试一下企业级项…...
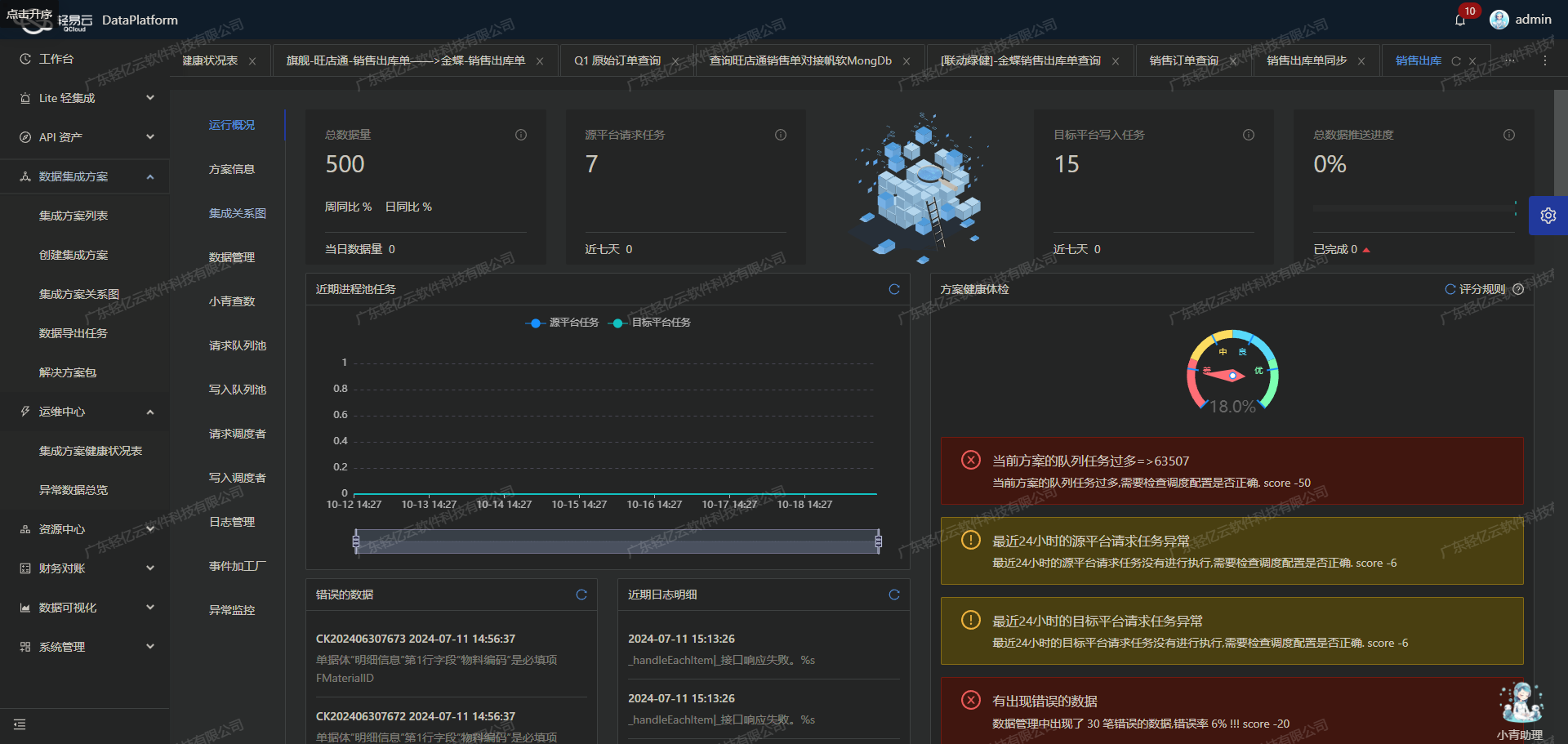
钉钉与金蝶云星空数据集成:提高企业付款申请单处理效率
钉钉数据集成到金蝶云星空:付款申请单的自动下推生成 在企业日常运营中,如何高效地管理和处理付款申请单是一个关键问题。为了提升这一流程的效率,我们采用了轻易云数据集成平台,将钉钉中的付款申请单数据无缝对接到金蝶云星空系…...
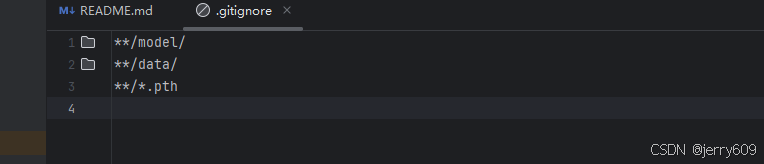
GIT使用list
清空当前commit区 方法 1:软重置到初始状态 如果希望保留文件内容,但清空所有 commit 历史,可以使用以下命令: git reset --soft $(git rev-list --max-parents0 HEAD)解释: --soft 表示重置 commit 历史ÿ…...

JavaSE:数组深入学习与复习
学习参考 1、可变参数传递 数组可以是int等基本数据类型,也可以是String等引用类型 package com.test;public class Main {public static void main(String [] args){int [] a {1,2,3,4,5};test(78,90,12,34,56,78,90,12,34,56,78);}public static void test(i…...

Redis 事务 总结
前言 相关系列 《Redis & 目录》(持续更新)《Redis & 事务 & 源码》(学习过程/多有漏误/仅作参考/不再更新)《Redis & 事务 & 总结》(学习总结/最新最准/持续更新)《Redis & 事务…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
