uni-app 获取 android 手机 IMEI码
1、需求来源
最近项目上需要获取手机的IMEI码,并且在更换手机号登录后,需要提示重新更新IMEI码。
2、需求拆分
2.1 获取 IMEI 码
查阅 uni-app 官网发现在android 10 已经无法获取imei码,所以对于这个需求拆分成两种情况。

第一种情况: android 10 以上 选择用户手动输入的方式。
第二种情况:android 10 以下,通过 plus.device.getInfo 自动获取的方式。

2.2 获取android 手机的唯一编码
2.2.1 通过 uni.getSystemInfoSync 获取
let { deviceId } = uni.getSystemInfoSync();

可以看出 deviceId 在清理缓存等情况下,会存在不唯一的情况。
2.2.2 通过 plus.device.getOAID 获取

可以发现该方法只会在android 10 以上的手机手机有效。
2.2.3 通过 plus.device.getInfo 获取
plus.device.getInfo 方法的使用方法同 2.1 过去 IMEI码
3、完整示例
3.1 获取 IMEI码,deviceId
/** * 获取系统设备信息 */ export function getSystemDeviceInfo() { return new Promise((resolve, reject) => { // 返回结果 let resolveResult = (deviceId, imei) => { resolve({ deviceId, imei }) }; let sysInfo = uni.getSystemInfoSync(); // #ifdef APP-PLUS if (sysInfo.osName.toLowerCase() == 'android' && sysInfo.osVersion >= 10) { plus.device.getOAID({ success: ({ oaid }) => { resolveResult(oaid); }, fail: (e) => { resolveResult(sysInfo.deviceId); } }); } else { requestPermissions(['android.permission.READ_PHONE_STATE']).then(res => { plus.device.getInfo({ success: ({ uuid, imei }) => { let [oaid] = uuid?.split(",") || [] resolveResult(oaid || sysInfo.deviceId, imei) }, fail: (error) => { resolveResult(sysInfo.deviceId); }, }); }).catch((err) => { resolveResult(sysInfo.deviceId); }); } // #endif // #ifndef APP-PLUS resolveResult(sysInfo.deviceId); // #endif }); }
3.2 申请系统权限
/** * 申请权限 * * @param {Object} permissions */ export function requestPermissions(permissions) { return new Promise((resolve, reject) => { plus.android.requestPermissions(permissions, function(e) { if (e.deniedAlways.length > 0) { //权限被永久拒绝 // 弹出提示框解释为何需要定位权限,引导用户打开设置页面开启 console.log('Always Denied!!! ' + e.deniedAlways.toString()); return reject({ code: -1, message: '权限被永久拒绝', deniedAlways: e.deniedAlways }); } if (e.deniedPresent.length > 0) { //权限被临时拒绝 // 弹出提示框解释为何需要定位权限,可再次调用plus.android.requestPermissions申请权限 console.log('Present Denied!!! ' + e.deniedPresent.toString()); return reject({ code: -2, message: '权限被临时拒绝', deniedAlways: e.deniedPresent }); } if (e.granted.length > 0) { // 权限被允许 // 调用依赖获取定位权限的代码 console.log('Granted!!! ' + e.granted.toString()); return resolve(); } }, function(e) { console.log('Request Permissions error:' + JSON.stringify(e)); reject(e); }); }); }
4、注意
1、plus.device.getInfo 在用户拒绝权限后success, fail 回调都不会响应,所以增加手动获取权限方法,避免用户拒绝权限后无法正确的回调
2、plus.device.getOAID 只在 android 10 以上有用。
3、uni.getSystemInfoSync 获取的 deviceId 存在不是唯一的情况。
相关文章:

uni-app 获取 android 手机 IMEI码
1、需求来源 最近项目上需要获取手机的IMEI码,并且在更换手机号登录后,需要提示重新更新IMEI码。 2、需求拆分 2.1 获取 IMEI 码 查阅 uni-app 官网发现在android 10 已经无法获取imei码,所以对于这个需求拆分成两种情况。 第一种情况&am…...
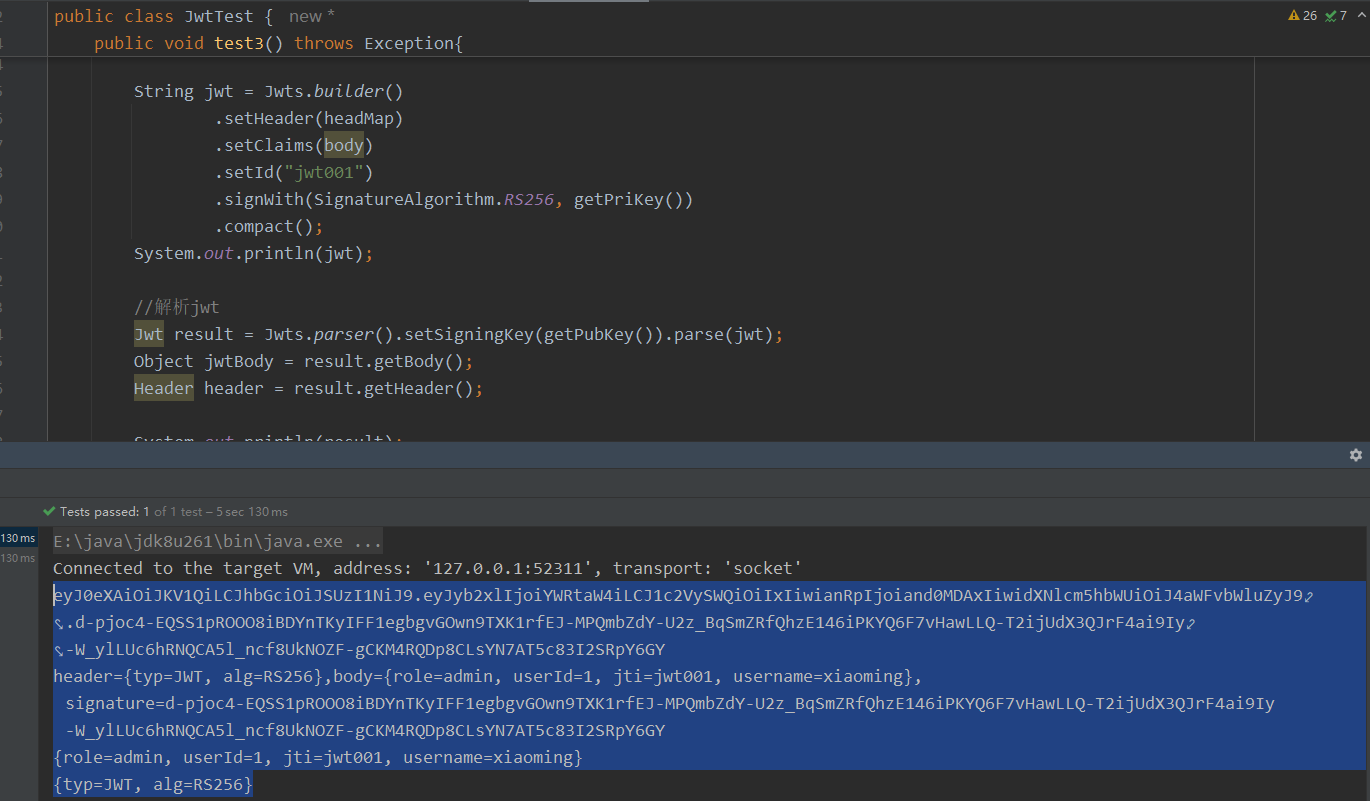
后台管理系统的通用权限解决方案(八)认证机制介绍、JWT介绍与jjwt框架的使用
文章目录 1 认证机制介绍1.1 HTTP Basic Auth1.2 Cookie-Session Auth1.3 OAuth1.4 Token Auth 2 JWT2.1 JWT介绍2.2 JWT的数据结构2.2.1 JWT头2.2.2 JWT有效载荷2.2.3 JWT签名 3 jjwt3.1 jjwt介绍3.2 jjwt案例 1 认证机制介绍 1.1 HTTP Basic Auth HTTP Basic Auth 是一种简…...

接口测试 —— Postman 变量了解一下!
Postman变量是在Postman工具中使用的一种特殊功能,用于存储和管理动态数据。它们可以用于在请求的不同部分、环境或集合之间共享和重复使用值。 Postman变量有以下几种类型: 1、环境变量(Environment Variables): 环境变量是在…...

鸿蒙系统:核心特性、发展历程与面临的机遇与挑战
好动与不满足是进步的第一必需品 文章目录 前言重要特点和组成部分核心特性主要组件发展历程 机遇挑战总结 前言 鸿蒙系统(HarmonyOS)是由华为技术有限公司开发的一款面向全场景的分布式操作系统。它旨在为用户提供更加流畅、安全且高效的数字生活体验&…...
从0到1,用Rust轻松制作电子书
我之前简单提到过用 Rust 做电子书,今天分享下如何用Rust做电子书。制作电子书其实用途广泛,不仅可以用于技术文档(对技术人来说非常方便),也可以制作用户手册、笔记、教程等,还可以应用于文学创作。 如果…...

半天入门!锂电池剩余寿命预测(Python)
往期精彩内容: 时序预测:LSTM、ARIMA、Holt-Winters、SARIMA模型的分析与比较 全是干货 | 数据集、学习资料、建模资源分享! EMD变体分解效果最好算法——CEEMDAN(五)-CSDN博客 拒绝信息泄露!VMD滚动分…...

学生党头戴式耳机哪款音质更胜一筹?TOP4好音质头戴式耳机推荐
在挑选头戴式耳机时,市场上琳琅满目的品牌和型号常常让人目不暇接。究竟哪个学生党头戴式耳机哪款音质更胜一筹?这已成为许多人面临的难题。由于每个人对耳机的偏好各有侧重——一些人追求音质的纯净,一些人重视佩戴的舒适性,而另…...

数据结构 ——— 二叉树的概念及结构
目录 二叉树的概念 特殊的二叉树 一、满二叉树 二、完全二叉树 二叉树的概念 二叉树树示意图: 从以上二叉树示意图可以看出: 二叉树每个节点的度不大于 2 ,那么整个二叉树的度也不大于 2 ,但是也不是每个节点都必须有 2 个…...

【React】React 的核心设计思想
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 React 的核心设计思想引言声明式编程声明式 vs 命令式示例 组件化组件的优势组件…...

C++ 二叉树进阶:相关习题解析
目录 1. 二叉树创建字符串。 2. 二叉树的分层遍历1 3. 二叉树的分层遍历2 4. 二叉树的最近公共祖先 5. 将二叉搜索树转换为排序的双向链表 6. 从前序与中序遍历序列构造二叉树 7. 从中序与后序遍历序列构造二叉树 8. 二叉树的前序遍历,非递归迭代实现 9.…...

Matlab实现蚁群算法求解旅行商优化问题(TSP)(理论+例子+程序)
一、蚁群算法 蚁群算法由意大利学者Dorigo M等根据自然界蚂蚁觅食行为提岀。蚂蚁觅食行为表示大量蚂蚁组成的群体构成一个信息正反馈机制,在同一时间内路径越短蚂蚁分泌的信息就越多,蚂蚁选择该路径的概率就更大。 蚁群算法的思想来源于自然界蚂蚁觅食&a…...

2024年10月HarmonyOS应用开发者基础认证全新题库
注意事项:切记在考试之外的设备上打开题库进行搜索,防止切屏三次考试自动结束,题目是乱序,每次考试,选项的顺序都不同 这是基础认证题库,不是高级认证题库注意看清楚标题 高级认证题库地址:20…...

kafka 分布式(不是单机)的情况下,如何保证消息的顺序消费?
大家好,我是锋哥。今天分享关于【kafka 分布式(不是单机)的情况下,如何保证消息的顺序消费?】面试题?希望对大家有帮助; kafka 分布式(不是单机)的情况下,如何保证消息的…...

数据分析案例-苹果品质数据可视化分析+建模预测
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

沈阳乐晟睿浩科技有限公司抖音小店运营创新
在当今这个数字化迅猛发展的时代,电子商务已经成为推动经济增长的重要引擎。而在电商的广阔舞台上,短视频与直播带货的崛起无疑是最为耀眼的明星之一。作为这一领域的佼佼者,抖音小店凭借其庞大的用户基础和独特的算法优势,吸引了…...

【前端】CSS知识梳理
基础:标签选择器、类选择器、id选择器和通配符选择器 font:font-style(normal) font-weight(400) font-size(16px) /line-height(0) font-family(宋体) 复合: 后代选择器( )、子选择器(>)、并集选择器(…...

【undefined reference to xxx】zookeeper库编译和安装 / sylar项目ubuntu20系统编译
最近学习sylar项目,编译项目时遇到链接库不匹配的问题,记录下自己解决问题过程,虽然过程很艰难,但还是解决了,以下内容供大家参考! undefined reference to 问题分析 项目编译报错 /usr/bin/ld: ../lib/lib…...

IDEA解决 properties 文件乱码问题
博主介绍: 计算机科班人,全栈工程师,掌握C、C#、Java、Python、Android等主流编程语言,同时也熟练掌握mysql、oracle、sqlserver等主流数据库,具有丰富的项目经验和开发技能。提供相关的学习资料、程序开发、技术解答、…...

超越Jira?2024年探索项目管理新工具!
一、Jira 在项目管理中的地位 Jira 作为一款在项目管理领域久负盛名的工具,有着不可忽视的地位。它以强大的问题跟踪和管理功能著称,无论是软件缺陷、新功能需求、任务分配还是技术难题的解决,都能精准把控。其高可定制性更是满足了不同团队…...

大模型,多模态大模型面试问题【计算图,LLama,交叉熵,SiLU,RLHF】
大模型,多模态大模型面试问题【计算图,LLama,交叉熵,SiLU,RLHF】 问题一:讲一讲计算图中pytorch是什么,TensorFlow是什么?1. PyTorch2. TensorFlow区别总结 问题二:Llama…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
