Cow Acrobats ( 临项交换贪心 )
题目大意:
N 头牛 , 每头牛有一个重量(Weight)和一个力量(Strenth) , N头牛进行排列 , 第 i 头牛的风险值为其上所有牛总重减去自身力量 , 问如何排列可以使最大风险值最小 , 求出这个最小的最大风险值;
思路:临项交换
邻项交换排序是一种常见的贪心算法,通过比较两个相邻元素交换前后的优劣对整个序列进行排序,从而使得这个序列成为题目所求的最优解。
我们假设前 i 项已经是最优排列 , 且第 i + 1 项和第 i + 2 项当前排列时最优
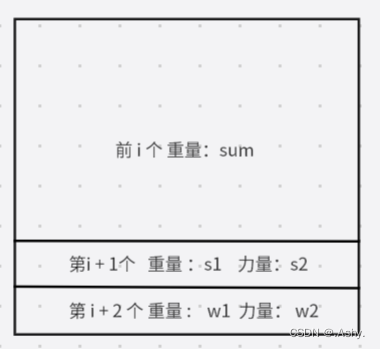
那么对于第 i + 1 个
resi+1=sum−s2res_{i+1} = sum - s_2resi+1=sum−s2
对于第 i + 2 个
resi+2=sum+s1−w2res_{i+2} = sum + s_1 - w_2resi+2=sum+s1−w2
若我们交换第 i + 1 项 和 第 i + 2 项
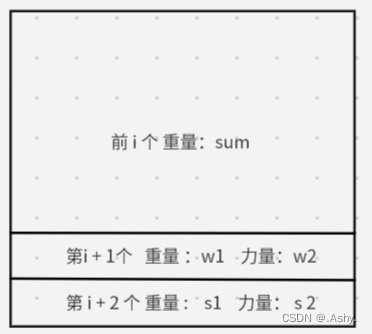
那么对于第 i + 1 个
resi+1′=sum−w2res_{i+1}'= sum - w_2resi+1′=sum−w2
对于第 i + 2 个
resi+2′=sum+w1−s2res_{i+2}' = sum + w_1 - s_2resi+2′=sum+w1−s2
在这里我们已经假设交换前为最优状态 , 所以我们根据题目中最大值最小的定义可以得到下面这个式子
max(resi+1,resi+2)<=max(resi+1′,resi+2′)max(res_{i+1} , res_{i+2}) <= max(res_{i+1}' , res_{i+2}')max(resi+1,resi+2)<=max(resi+1′,resi+2′)
转化一下
max(sum−s2,sum+s1−w2)<=max(sum−w2,sum+w1−s2)max(sum - s_2 , sum + s_1 - w_2) <= max(sum - w_2 , sum + w_1 - s_2)max(sum−s2,sum+s1−w2)<=max(sum−w2,sum+w1−s2)
每一项 减去 sum 加上 (s2+w2s_2 + w_2s2+w2)
max(w2,s1+s2)<=max(s2,w1+w2)max(w_2 , s_1 + s_2) <= max(s_2 , w_1 + w_2)max(w2,s1+s2)<=max(s2,w1+w2)
至此 , 我们就推出了我们想要的交换方程
bool cmp(node a,node b){return max(a.x + a.y , b.y) < max(b.x + b.y , a.y) || (max(a.x + a.y , b.y) == max(b.x + b.y , a.y) && a.x + a.y < b.x + b.y);
}
这里等于号要特判 ,不懂的可以看看下面这个博客
浅谈邻项交换排序的应用以及需要注意的问题
当我们排好序后 ,不要忘记我们的问题 , 是要求最小的最大值 ,这是只要遍历所有状态求出最大值即可。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef long long ll;
const int N = 2e5+10;
const int p = 1e9 + 7;
typedef pair<int,int>PII;
const int inf = 1 << 31 - 1;
const double eps = 1e-9;int n;struct node{int x,y;
}a[N];bool cmp(node a,node b){return max(a.x + a.y , b.y) < max(b.x + b.y , a.y) || (max(a.x + a.y , b.y) == max(b.x + b.y , a.y) && a.x + a.y < b.x + b.y);
}int main(){IOScin >> n;for(int i=1;i<=n;i++){cin >> a[i].x >> a[i].y;}sort(a+1,a+1+n,cmp);int ans = -inf , sum = 0;for(int i=1;i<=n;i++){sum += a[i-1].x;ans = max(ans , sum - a[i].y);}cout << ans ;return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);相关文章:

Cow Acrobats ( 临项交换贪心 )
题目大意: N 头牛 , 每头牛有一个重量(Weight)和一个力量(Strenth) , N头牛进行排列 , 第 i 头牛的风险值为其上所有牛总重减去自身力量 , 问如何排列可以使最大风险值最小 , 求出这个最小的最大风险值&am…...

MySQL:为什么说应该优先选择普通索引,尽量避免使用唯一索引
前言 在使用MySQL的过程中,随着表数据的逐渐增多,为了更快的查询我们需要的数据,我们会在表中建立不同类型的索引。 今天我们来聊一聊,普通索引和唯一索引的使用场景, 以及为什么说推荐大家优先使用普通索引…...

Spring Cloud alibaba之Feign
JAVA项目中如何实现接口调用?HttpclientHttpclient是Apache Jakarta Common下的子项目,用来提供高效的、最新的、功能丰富的支持Http协议的客户端编程工具包,并且它支持HTTP协议最新版本和建议。HttpClient相比传统JDK自带的URL Connection&a…...
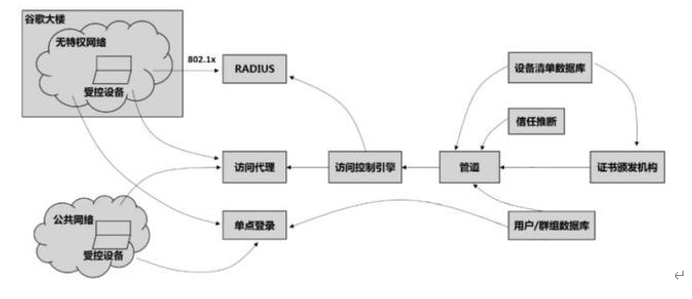
零信任-Google谷歌零信任介绍(3)
谷歌零信任的介绍? "Zero Trust" 是一种网络安全模型,旨在通过降低网络中的信任级别来防止安全威胁。在零信任模型中,不论请求来自内部网络还是外部网络,系统都将对所有请求进行详细的验证和审核。这意味着每次请求都需…...
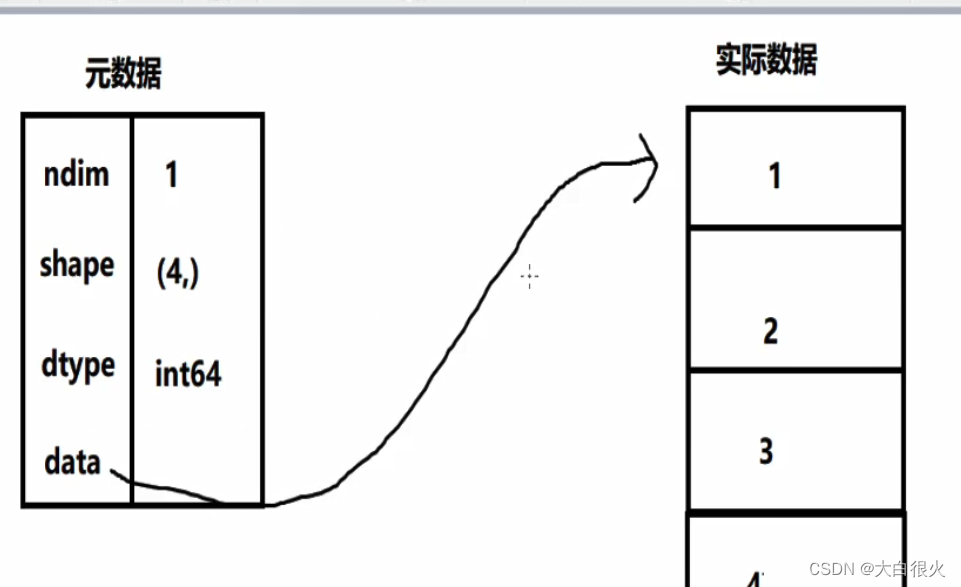
Numpy基础——人工智能基础
文章目录一、Numpy概述1.优势2.numpy历史3.Numpy的核心:多维数组4.numpy基础4.1 ndarray数组4.2 内存中的ndarray对象一、Numpy概述 1.优势 Numpy(Nummerical Python),补充了Python语言所欠缺的数值计算能力;Numpy是其它数据分析及机器学习库的底层库&…...

电商仓储与配送云仓是什么?
仓库是整个供给链的关键局部。它们是产品暂停和触摸的点,耗费空间和时间(工时)。空间和时间反过来也是费用。经过开发数学和计算机模型来微调仓库的规划和操作,经理能够显著降低与产品分销相关的劳动力本钱,进步仓库空间应用率,并…...

【零基础入门前端系列】—HTML介绍(一)
【零基础入门前端系列】—HTML介绍(一) 一、什么是HTML HTML是用来描述网页的一种语言HTML指的是超文本标记语言:HyperText Markup LanguageHTML不是一种编程语言,而是一种超文本标记语言,标记语言是一套标记标签(ma…...

Elasticsearch索引库和文档的相关操作
前言:最近一直在复习Elasticsearch相关的知识,公司搜索相关的技术用到了这个,用公司电脑配了环境,借鉴网上的课程进行了总结。希望能够加深自己的印象以及帮助到其他的小伙伴儿们😉😉。 如果文章有什么需要…...

使用Python,Opencv检测图像,视频中的猫
使用Python,Opencv检测图像,视频中的猫🐱 这篇博客将介绍如何使用Python,OpenCV库附带的默认Haar级联检测器来检测图像中的猫。同样的技术也可以应用于视频流。这些哈尔级联由约瑟夫豪斯(Joseph Howse)训练…...

浅谈域名和服务器集约化管理的误区
一个正常的网站通常由域名、网站程序、服务器三个部分组成,网站程序由单位开发设计,而域名和服务器则需要租用购买,那么域名和服务器之间的关系是什么?如何实现域名和服务器的有效管理呢? 服务器和域名的关系 服务器…...

迪赛智慧数——柱状图(正负条形图):20212022人才求职最关注的因素
效果图从近两年职场跳槽方向看,相比此前人们对高薪大厂趋之若鹜,如今职场人更关注业务前景。根据相关数据显示,职场人求职最关注的因素中,“薪资福利”权重下降,“个人发展”权重上升,“业务前景”首次进入…...

网络安全-黑帽白帽红客与网络安全法
网络安全-黑帽白帽红客与网络安全法 本章内容较少,因为刚开端。 黑客来源于hacker 指的是信息安全里面,能够自由出入对方系统,指的是擅长IT技术的电脑高手 黑帽黑客-坏蛋,研究木马的,找漏洞的,攻击网络或者…...

Xpath元素定位之同级节点,父节点,子节点
XPath学习:轴(8)——following-siblingXPath 是一门在 XML 文档中查找信息的语言。XPath 可用来在 XML 文档中对元素和属性进行遍历。XPath 是 W3C XSLT 标准的主要元素,并且 XQuery 和 XPointer 同时被构建于 XPath 表达之上。推荐一个挺不错的网站:htt…...
| 真题+思路+代码)
华为OD机试 - 挑选字符串(Python)| 真题+思路+代码
挑选字符串 题目 给定 a-z,26 个英文字母小写字符串组成的字符串 A 和 B, 其中 A 可能存在重复字母,B 不会存在重复字母, 现从字符串 A 中按规则挑选一些字母可以组成字符串 B 挑选规则如下: 同一个位置的字母只能挑选一次, 被挑选字母的相对先后顺序不能被改变, 求最…...
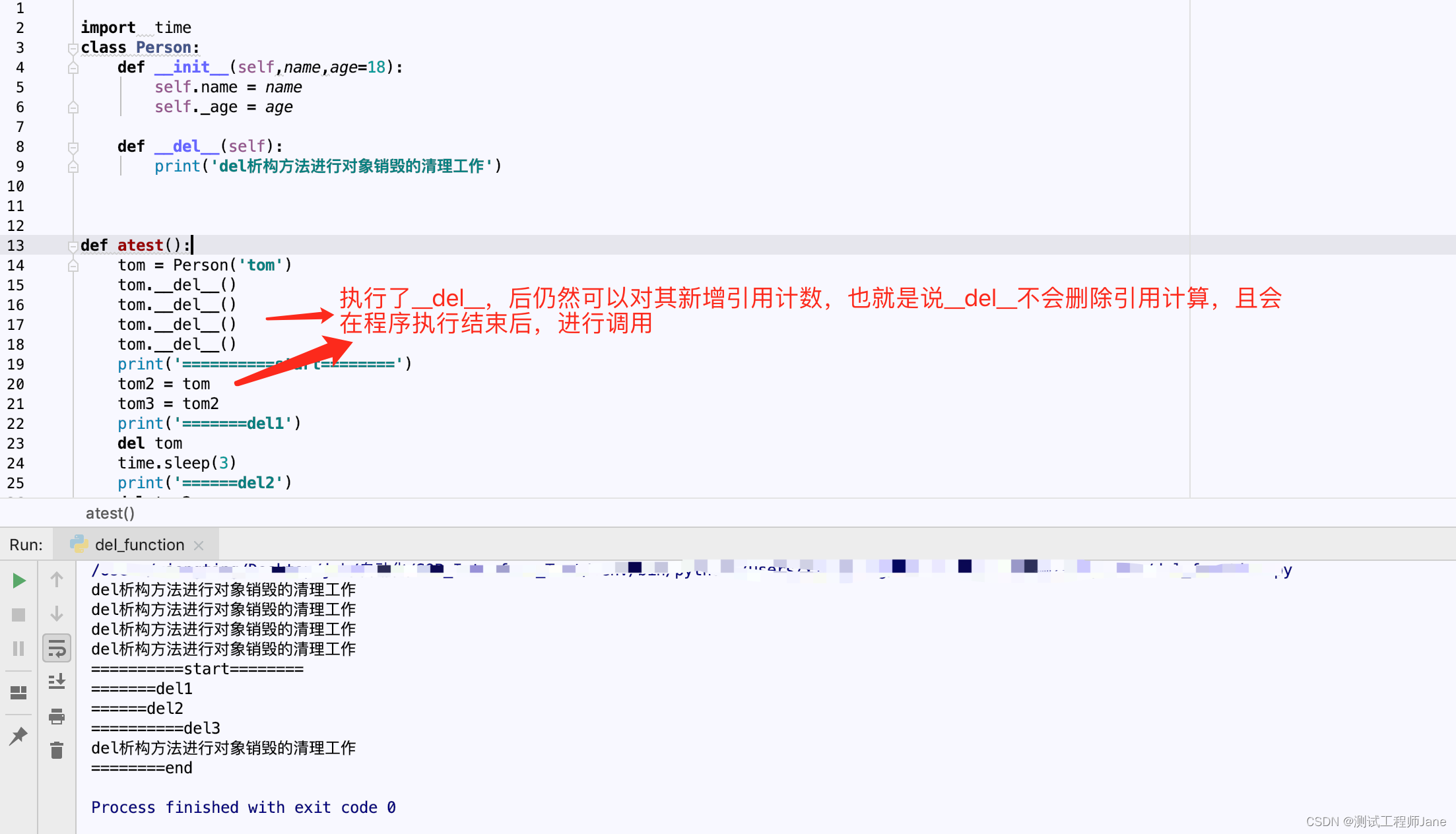
python笔记-- “__del__”析构方法
-#### 1、基本概念(构造函数与析构函数) 特殊函数:由系统自动执行,在程序中不可显式地调用他们 构造函数: 建立对象时对对象的数据成员进行初始化(对象初始化) 析构函数: 对象生命期…...

支付系统核心架构设计思路(万能通用)
文章目录1. 支付系统总览核心系统交互业务图谱2. 核心系统解析交易核心交易核心基础交易类型抽象多表聚合 & 订单关联支付核心支付核心总览支付行为编排异常处理渠道网关资金核算3. 服务治理平台统一上下文数据一致性治理CAS校验幂等 & 异常补偿对账准实时对账DB拆分异…...

python实现mongdb的双活
如何用python实现mongdb的双活,两个数据库实时同步? 可以使用Pymongo库,它可以提供同步的API来实现MongoDB的双活,两个数据库实时同步。还可以使用MongoDB的复制集功能来进行实时同步。 Pymongo库提供什么同步的API来实现MongoD…...
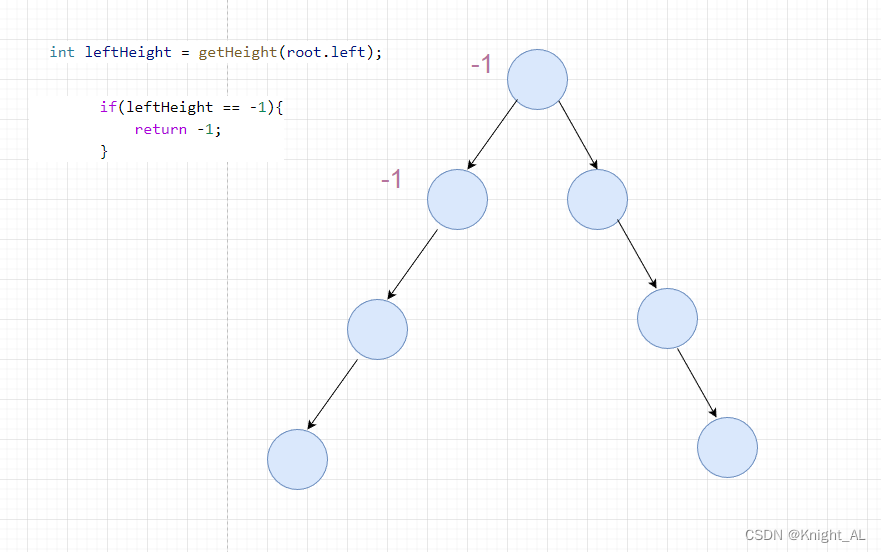
LeetCode-110. 平衡二叉树
目录题目分析递归法题外话题目来源 110. 平衡二叉树 题目分析 平很二叉树:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 二叉树节点的深度和二叉树节点的高度 递归法 递归三步曲 1.明确递归函数的参数和返回值 参数:当前传入节点。 返回值…...

Python蓝桥杯训练:基本数据结构 [链表]
Python蓝桥杯训练:基本数据结构 [链表] 文章目录Python蓝桥杯训练:基本数据结构 [链表]一、链表理论基础知识二、有关链表的一些常见操作三、力扣上面一些有关链表的题目练习1、[移除链表元素](https://leetcode.cn/problems/remove-linked-list-element…...
| 真题+思路+代码)
华为OD机试 - 找字符(Python)| 真题+思路+代码
找字符 题目 给定两个字符串, 从字符串2中找出字符串1中的所有字符, 去重并按照 ASCII 码值从小到大排列。 输入 字符范围满足 ASCII 编码要求, 输入字符串1长度不超过1024, 字符串2长度不超过100。 输出描述 按照 ASCII 由小到大排序 示例一 输入 bach bbaaccddf…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
