背包问题(三)
文章目录
- 一、二维费用的背包问题
- 二、潜水员
- 三、机器分配
- 四、开心的金明
- 五、有依赖的背包问题
一、二维费用的背包问题
题目链接

#include<iostream>
#include<algorithm>
using namespace std;
const int M = 110;
int n,m,kg;
int f[M][M];int main()
{cin >> n >> m >> kg;for(int i = 0;i < n;i ++){int v,M,w;cin >> v >> M >> w;for(int j = m;j >= v;j --)for(int k = kg;k >= M;k --){f[j][k] = max(f[j][k], f[j - v][k - M] + w);}}cout << f[m][kg];return 0;
}
二、潜水员
题目链接

题解来源:小呆呆 ,
这个题相较于二维费用的背包问题,稍稍有一点改变,二维费用的背包模板是体积不超过V,重量不超过M,但是这个题是体积至少为V,重量至少为M。
对比两题的思路,二维费用的背包问题,求的是不能超过体积V,重量M的情况下,能拿到价值的最大值。而本题是至少需要体积V,重量M的情况下,能拿到价值的最小值。就拿体积来说,至少需要多少体积,也就是说有体积比需要的体积大的物品还是能用得到,例如f[3][5],至少需要3个体积,5个重量,求能拿到价值的最小值,现在只有一个物品,体积是4,重量是4,价值w,它说至少需要3个体积,那么体积是4还是可以用到,只是多了1个体积没用占着而已,不影响其价值。因此若用了这个物品,则变成了求f[0][1] + w,表示体积已经不再需求了,只需要0个体积即可
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;int n,m,k;
const int M = 25, N = 82;
int f[M][N];
const int INF = 0x3f3f3f3f;int main()
{cin >> m >> n;cin >> k;memset(f, 0x3f, sizeof f);f[0][0] = 0;for(int i = 1;i <= k;i ++){int a,b,c;cin >> a >> b >> c;for(int j = m;j >= 0;j --)for(int x = n;x >= 0;x --){f[j][x] = min(f[j][x], f[max(0,j - a)][max(0, x - b)] + c);}}cout << f[m][n];return 0;
}
三、机器分配
题目链接


#include<iostream>
#include<algorithm>
using namespace std;int n,m;
const int N = 12, M = 18;
int f[N][M];
int ne[M];
int w[N][M];
int way[M];int main()
{cin >> n >> m;for(int i = 1;i <= n;i ++)for(int j = 1;j <= m;j ++)cin >> w[i][j];for(int i = 1;i <= n;i ++){for(int j = 0;j <= m;j ++){for(int k = m;k >= j;k --)f[i][k] = max(f[i][k], f[i - 1][k - j] + w[i][j]);}}cout << f[n][m] << endl;int j = m;for(int i = n;i >= 1;i --)for(int k = 0;k <= m;k ++)if(f[i][j] == f[i - 1][j - k] + w[i][k]){way[i] = k;j -= k;break;}for(int i = 1;i <= n;i ++) cout << i << " " << way[i] << endl;return 0;
}
四、开心的金明

这个题很容易,就是一个01背包问题
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 30100;
int n,m;
int f[N];int main()
{cin >> n >> m;for(int i = 1;i <= m;i ++){int v,w;cin >> v >> w;for(int j = n;j >= v;j --)f[j] = max(f[j], f[j - v] + v * w);}cout << f[n];return 0;
}
五、有依赖的背包问题
题目链接


#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int head[N],e[N],ne[N],idx;
int n,m;
int v[N],w[N],p;
bool st[N];
int f[N][N];void add(int a,int b)
{e[idx] = b, ne[idx] = head[a], head[a] = idx ++;
}void dfs(int u)
{for(int i = head[u]; ~i;i = ne[i]){int son = e[i];dfs(e[i]);for(int j = m - v[u];j >= 0;j --){for(int k = 0;k <= j;k ++)f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);}}for(int i = m;i >= v[u];i --) f[u][i] = f[u][i - v[u]] + w[u];for(int i = 0;i < v[u];i ++) f[u][i] = 0;
}int main()
{cin >> n >> m;memset(head, -1,sizeof head);int root;for(int i = 1;i <= n;i ++){cin >> v[i] >> w[i] >> p;if(p == -1) { root = i;continue;}add(p, i);st[i] = true;}dfs(root);cout << f[root][m];return 0;
}
相关文章:

背包问题(三)
文章目录 一、二维费用的背包问题二、潜水员三、机器分配四、开心的金明五、有依赖的背包问题 一、二维费用的背包问题 题目链接 #include<iostream> #include<algorithm> using namespace std; const int M 110; int n,m,kg; int f[M][M];int main() {cin >…...

linux之调度管理(2)-调度器 如何触发运行
一、调度器是如何在程序稳定运行的情况下进行进程调度的 1.1 系统定时器 因为我们主要讲解的是调度器,而会涉及到一些系统定时器的知识,这里我们简单讲解一下内核中定时器是如何组织,又是如何通过通过定时器实现了调度器的间隔调度。首先我们…...

深入理解 Vue 3 中的 Props
深入理解 Vue 3 中的 Props Vue 3 引入了 Composition API 等新特性,组件的定义和使用也变得更为灵活。而在组件通信中,Props(属性)扮演了重要角色,帮助父组件向子组件传递数据,形成单向的数据流动&#x…...

校园周边美食探索及分享平台
摘要: 美食一直是与人们日常生活息息相关的产业。传统的电话订餐或者到店消费已经不能适应市场发展的需求。随着网络的迅速崛起,互联网日益成为提供信息的最佳俱渠道和逐步走向传统的流通领域,传统的美食业进而也面临着巨大的挑战࿰…...

内网对抗-信息收集篇SPN扫描DC定位角色区域定性服务探针安全防护凭据获取
知识点: 1、信息收集篇-网络架构-出网&角色&服务&成员 2、信息收集篇-安全防护-杀毒&防火墙&流量监控 3、信息收集篇-密码凭据-系统&工具&网站&网络域渗透的信息收集: 在攻防演练中,当完成边界突破后进入内…...

石墨舟氮气柜:半导体制造中的关键保护设备
石墨舟是由高纯度石墨材料制成的,主要用于承载硅片或其他基板材料通过高温处理过程,是制造半导体器件和太阳能电池片的关键设备之一。 石墨舟在空气中容易与氧气发生反应,尤其是在高温处理后,表面可能更为敏感;石墨舟具…...

性能调优专题(7)之Innodb底层原理与Mysql日志机制深入剖析
一、MYSQL的内部组件结构 大体来说,Mysql可以分为Server层和存储引擎层两部分。 1.1 Server层 Server层主要包括连接器、查询缓存、词法分析器、优化器等。涵盖MYSQL的大多数核心服务功能,以及所有的内置函数(如日期、时间、数学和加密函数等),所有跨存储引擎的功…...

量子计算及其在密码学中的应用
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 量子计算及其在密码学中的应用 量子计算及其在密码学中的应用 量子计算及其在密码学中的应用 引言 量子计算概述 定义与原理 发展…...
、Cuckoo Hashing详细解读)
LSM树 (Log-Structured Merge Tree)、Cuckoo Hashing详细解读
一、LSM 树 (Log-Structured Merge Tree) LSM 树(Log-Structured Merge Tree) 是一种专为 高效写入和批量更新 设计的数据结构,特别适合于 高写入密度 的应用场景,如数据库和文件系统。它广泛用于 NoSQL 数据库(如 Ca…...

VMware中的重要日志文件 vobd.log 学习总结
最近几天处理完毕存储的故障后,接着就是host方面的问题,Vmware无法访问到存储,其实存储的LUN和POOL 已经online ready了,但是主机还是访问不到存储。 这里介绍下Vmware中的一个重要的日志文件 vobd.log,该文件对于分析…...

MyBatis 返回 Map 或 List<Map>时,时间类型数据,默认为LocalDateTime,响应给前端默认含有‘T‘字符
一、问题 MyBatis 返回 Map 或 List时,时间类型数据,默认为LocalDateTime Springboot 响应给前端的LocalDateTime,默认含有’T’字符,如何统一配置去掉 二、解决方案 1、pom.xml 增加依赖(2024.11.6 补充ÿ…...

ASR TP
ASR翱捷科技 ASR kernel 5.10 android14 ASR EVB平台 jd9365tr(jadard) spi 1.驱动: 跟mtk驱动一样,放进去,不用改 asr_android14.0_alpha\asr\kernel\linux\drivers\input\touchscreen\jadard makefile: asr_android14.0_alpha\asr\kernel\linux\drivers\input\t…...

Tomcat与Nginx之全面比较
概况 Apache Tomcat Apache Tomcat,通常简称为Tomcat,是一个开源的Web应用服务器,它主要用于运行Java Web应用程序。Tomcat实现了Java Servlet和JavaServer Pages(JSP)技术,这些是Java EE规范的一部分。To…...

这是一个bug求助帖子--安装kali 遇坑
第一个报错 介质:kali-linux-2024.1-live-amd64 环境:Dell笔记本 i510代cpu 现象及操作 安装完以后 然后我换了个国内的源进行了以下操作 apt-get update:更新源列表 apt-get upgrade:更新所有可以更新的软件包 然后进行清理。…...

IntelliJ Idea设置自定义快捷键
我IDEA的快捷键是自己修改成了和Eclipse相似,然后想要跳转到某个方法的上层抽象方法没有对应的快捷键,IDEA默认的是Ctrl U (Windows/Linux 系统) 或 Command U (Mac 系统),但是我的不起作用&a…...
AlohaKit:一组.NET MAUI绘制的开源控件
前言 今天大姚给大家分享一组.NET MAUI绘制的开源、免费(MIT License)UI控件库:AlohaKit。 MAUI介绍 .NET MAUI是一个开源、免费(MIT License)的跨平台框架(支持Android、iOS、macOS 和 Windows多平台运…...
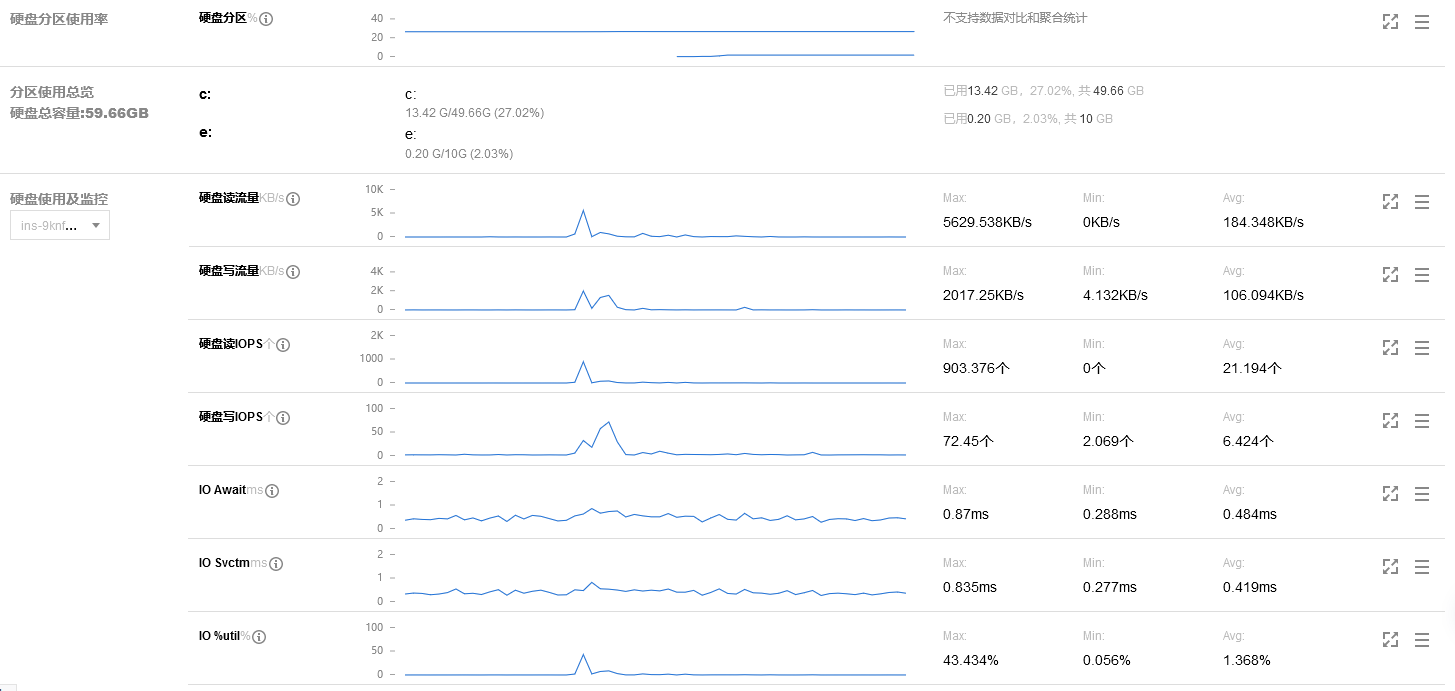
Windows 实例磁盘空间管理
操作场景 本文以操作系统为 Windows Server 2012 R2 的腾讯云云服务器为例,介绍如何在 Windows 实例磁盘空间不足的情况下进行空间释放操作,及如何进行磁盘的日常维护。 操作步骤 释放磁盘空间 您可通过 删除容量较大文件 或 删除不需要的文件 &…...

【动手学电机驱动】STM32-FOC(6)基于 IHM03 的无感方波控制
STM32-FOC(1)STM32 电机控制的软件开发环境 STM32-FOC(2)STM32 导入和创建项目 STM32-FOC(3)STM32 三路互补 PWM 输出 STM32-FOC(4)IHM03 电机控制套件介绍 STM32-FOC(5&…...

【数据结构】汇编语言和机器语言的‘数据结构‘
前言 汇编语言没有像高级语言(如 C#、Java 等)那样直接提供数据结构(如数组、链表、树、栈等),但是可以通过对内存地址和寄存器的操作来实现这些数据结构。汇编语言的核心是直接操控计算机的内存,因此所有…...

hadoop+spark中8088,18080,19888,4040端口页面的区别
在hadoop集群中,本身就有 9870端口,8088端口,19888端口 这三个页面,当使用spark作为计算引擎时,会多出8080,4040,18080这三个页面,页面就很多了,现在明确的辨别一下。 单…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
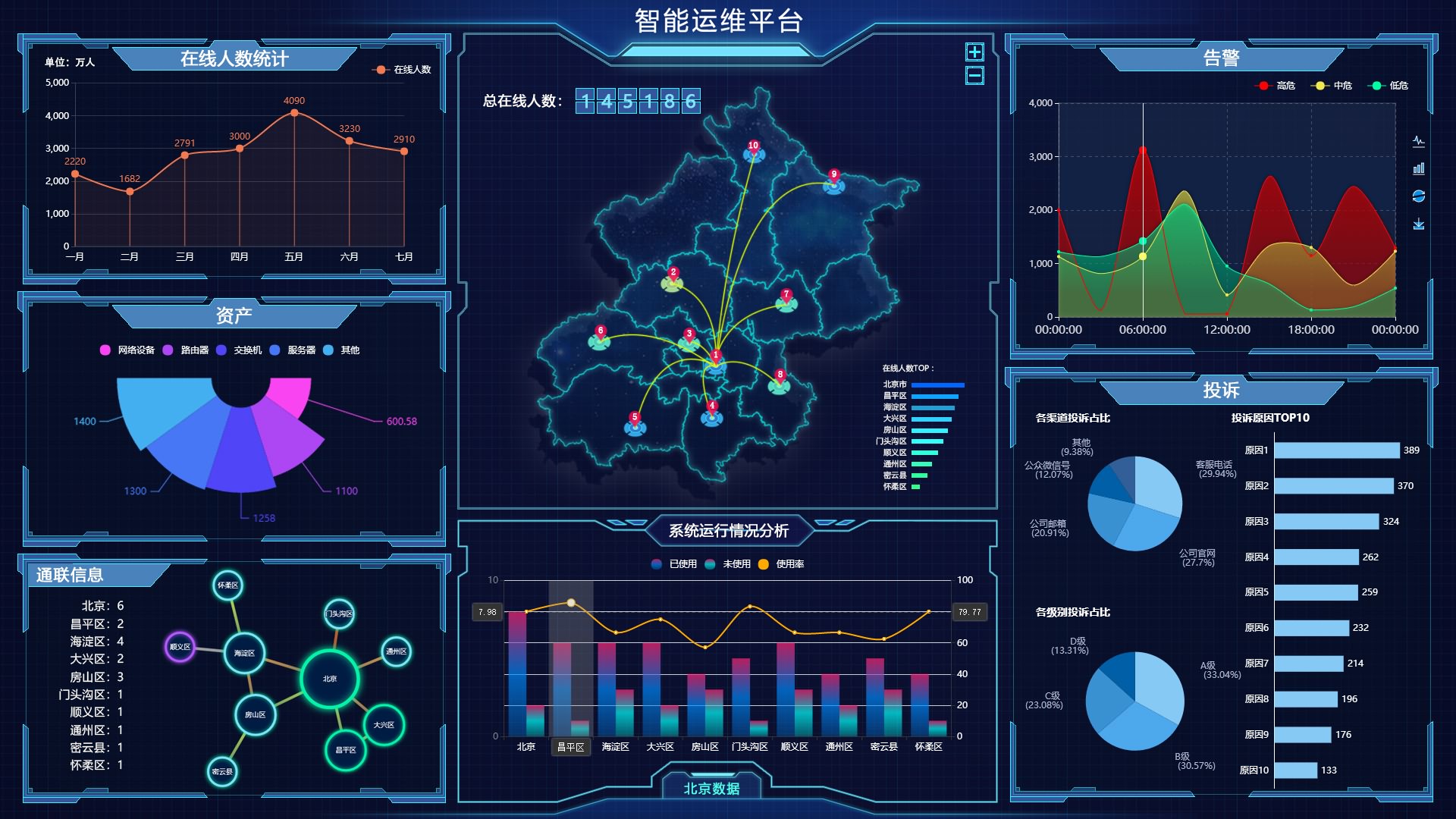
可视化预警系统:如何实现生产风险的实时监控?
在生产环境中,风险无处不在,而传统的监控方式往往只能事后补救,难以做到提前预警。但如今,可视化预警系统正在改变这一切!它能够实时收集和分析生产数据,通过直观的图表和警报,让管理者第一时间…...

python学习day39
图像数据与显存 知识点回顾 1.图像数据的格式:灰度和彩色数据 2.模型的定义 3.显存占用的4种地方 a.模型参数梯度参数 b.优化器参数 c.数据批量所占显存 d.神经元输出中间状态 4.batchisize和训练的关系 import torch import torchvision import torch.nn as nn imp…...
