[算法初阶]埃氏筛法与欧拉筛
素数的定义:
首先我们明白:素数的定义是只能整除1和本身(1不是素数)。
我们判断一个数n是不是素数时,可以采用试除法,即从i=2开始,一直让n去%i,直到i*i<=n
c语言:
#include<stdio.h>
int main()
{int n;for (int i = 2; i * i<= n; i++){if (n % i == 0){printf("%d 不是素数",n);return 0;}}printf("%d 是素数", n);
}C++:
#include<iostream>
using namespace std;
int main()
{int n;for (int i = 2; i * i<= n; i++){if (n % i == 0){cout<<n<<"不是素数";return 0;}}cout<<n<<"是素数";
}但是问题来了,如果一两个数让你去判断,你这么试除一下还行,那要是一堆大且多的荒谬的数据让你去判断,你需要循环的次数也是一个天文数字。这个时候,我们就可以通过一些算法来实现对于大数据(大且多)素数的判断。
埃筛与欧拉筛的实质:
其实埃筛与欧拉筛的实质都且就是围绕这一句话:素数的倍数不是素数。
比如说让你输出100000——1e5内所有的素数
那我们就筛就好啦,首先咱需要创建一个存素数的数组和一个bool类型的数组(用来判断该元素是否是素数)
埃氏筛:
//埃氏筛法
int n=1e5;
bool shai[n];
int cun[n];
signed main()
{int cnt = 0;for (int i = 2; i <= n; i++){if (!shai[i])//如果为0{cun[cnt++] = i;for (int j = 2; j <= n; j++){if (i * j > n)break;//超过数据大小就退掉。shai[i * j] = 1;//1的都是素数的倍数——所以不是素数。}}}for (int i = 0; i < cnt; i++){printf("%d ", cun[i]);}
}我们先看一看欧拉筛
欧拉筛:
#include<iostream>
using namespace std;
bool a[100001] = { 1,1 };//同上问一样i=0,i=1的时候都不是质数
int b[100001];//存质数
long long n;
int main()
{int cnt = 0;cin >> n;//查的范围for (int i = 2; i <= n; i++){if (a[i] == 0) b[++cnt] = i;for (int j = 1; j <= cnt; j++){if (i * b[j] > n)break;// 如果超出给出的范围,那么就退出循环 a[i * b[j]] = 1;//素数的倍数不是素数,进行标记。if (i % b[j] == 0)break;//超级关键的只标记一次}}for (int i = 1; i <= cnt; i++){printf("%d ", b[i]);}
}欧拉筛比埃筛要快很多很多
我们看看埃筛,就从2开始,它是素数,所以内循环会标记4,6,8,10,12······一直到退出循环,然后当外层循环到3的时候,它又会标记6,9,12······,在这里我们就能看出一点问题,有数被重新标记了,而且循环到后面重复标记的数量会很多,所以浪费了时间。
相关文章:

[算法初阶]埃氏筛法与欧拉筛
素数的定义: 首先我们明白:素数的定义是只能整除1和本身(1不是素数)。 我们判断一个数n是不是素数时,可以采用试除法,即从i2开始,一直让n去%i,直到i*i<n c语言: #include<…...

【THM】linux取证 DisGruntled
目录 0x00 房间介绍 0x01 连接并简单排查 0x02 让我们看看做没做坏事 0x03 炸弹已埋下。但何时何地? 0x04 收尾 0x05 结论 0x00 房间介绍 嘿,孩子!太好了,你来了! 不知道您是否看过这则新闻,我…...
)
SpringBoot整合Freemarker(四)
escape, noescape 语法 <#escape identifier as expression>...<#noescape>...</#noescape>... </#escape> 用例 主要使用在相似的字符串变量输出,比如某一个模块的所有字符串输出都必须是html安全的,这个时候就可以使用&am…...

centos docker 安装 rabbitmq
安装docker 1.更新现有的软件包 首先,确保您的系统是最新的,可以通过运行以下命令来实现: sudo yum update -y 2.移除旧版本的Docker 如果您之前安装过Docker,可能需要先卸载旧版本。使用以下命令来卸载旧版本的Docker&#…...

手动实现promise的all,race,finally方法
Promise.all 是一个非常有用的工具,它接受一个 Promise 对象数组,并返回一个新的 Promise。当所有输入的 Promise 都成功解决时,新的 Promise 会解决为一个包含所有结果的数组;如果任何一个 Promise 被拒绝,新的 Prom…...

H5移动端预览PDF方法
新建页面 新建一个页面以便去预览对应的pdf 新建完后在 pages.json 文件内去新增对应路由 页面内容 <template><view class"page"><view class"pdf"><view id"demo"></view></view><view class"b…...

uniapp—android原生插件开发(1环境准备)
本篇文章从实战角度出发,将UniApp集成新大陆PDA设备RFID的全过程分为四部曲,涵盖环境搭建、插件开发、AAR打包、项目引入和功能调试。通过这份教程,轻松应对安卓原生插件开发与打包需求! 项目背景: UniApp集成新大陆P…...

《潜行者2切尔诺贝利之心》游戏引擎介绍
潜行者2切尔诺贝利之心是基于虚幻5引擎,所以画面效果大家不必担心。游戏目前已经跳票了很久,预计发售时间是2024 年 11 月 21 日,这次应该不会再跳票。 潜行者2切尔诺贝利之心是虚幻5吗 答:是虚幻5。 潜行者官方推特之前回复了…...

winform 加载 office excel 插入QRCode图片如何设定位置
需求:winform 加载 office excel 并加载QRCode图片,但是每台PC打印出来QRCode位置都不太一样,怎么办呢? 我的办法: 1、在sheet中插入一个 textbox ,改名 qrcode (这个名字随便设置)…...

简易入手《SOM神经网络》的本质与原理
原创文章,转载请说明来自《老饼讲解神经网络》:www.bbbdata.com 关于《老饼讲解神经网络》: 本网结构化讲解神经网络的知识,原理和代码。 重现matlab神经网络工具箱的算法,是学习神经网络的好助手。 目录 一、入门原理解说 01.…...

21.assert断言
assert(断言)主要用于在程序运行过程中检查某个条件是否满足,如果不满足则会触发错误并终止程序执行,可以帮助程序员在开发阶段及时发现可能存在的逻辑错误等问题。 通过断言调试程序,abotr() has been called 就是断言…...

15分钟学 Go 第 46 天 : 监控与日志
第46天:监控与日志 学习目标 了解如何实现应用监控与日志管理,掌握相关工具和最佳实践。 内容结构 引言监控的概念与工具 监控的定义常见监控工具 日志管理的概念与工具 日志的重要性常见日志管理工具 实现监控与日志的最佳实践 监控指标日志格式 实战…...

BFS 算法专题(四):多源 BFS
目录 1. 01 矩阵 1.1 算法原理 1.2 算法代码 2. 飞地的数量 2.1 算法原理 2.2 算法代码 3. 地图中的最高点 3.1 算法原理 3.2 算法代码 4. 地图分析 4.1 算法原理 4.2 算法代码 1. 01 矩阵 . - 力扣(LeetCode) 1.1 算法原理 采用 BFS 正难…...
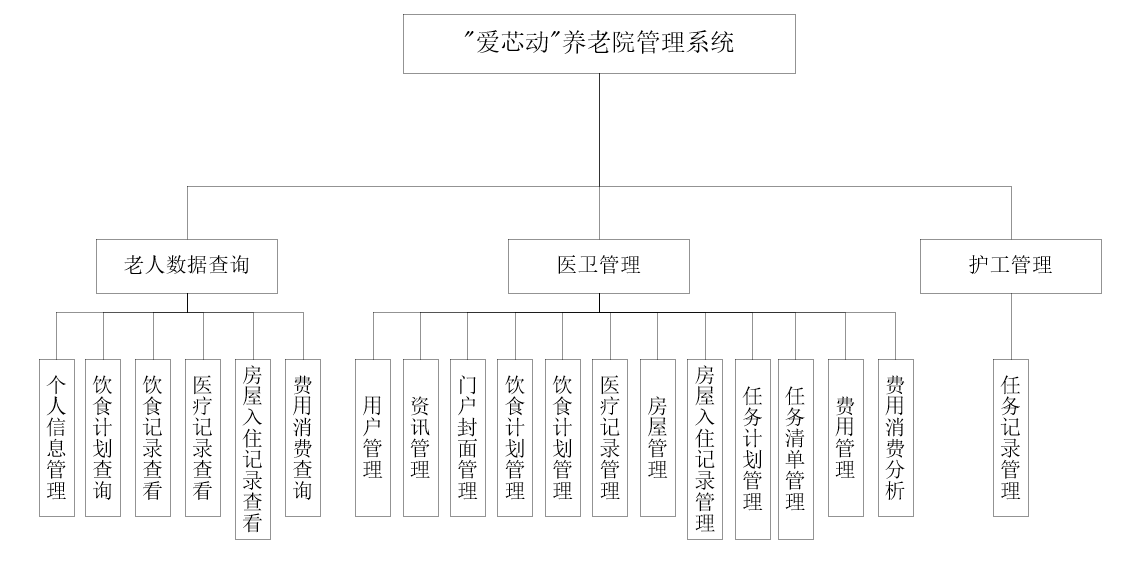
基于Spring Boot+Vue的养老院管理系统【原创】
一.系统开发工具与环境搭建 1.系统设计开发工具 后端使用Java编程语言的Spring boot框架 项目架构:B/S架构 运行环境:win10/win11、jdk17 前端: 技术:框架Vue.js;UI库:ElementUI; 开发工具&…...

Linux screen和cscope工具使用总结
1 minicom使用 1.1 minicom配置 第一次启动时: 如果输入sudo minicom提示错误,则需: sudo minicom -s 启动 出现配置菜单:选serial port setup 进入串口配置 输入A配置串口驱动为/dev/ttyUSB0 输入E配置速率为115200 8N1 输入F将 …...

深度学习面试八股汇总
按序发布: 深度学习——优化算法、激活函数、归一化、正则化 进入 深度学习——权重初始化、评估指标、梯度消失和梯度爆炸 进入 深度学习——前向传播与反向传播、神经网络(前馈神经网络与反馈神经网络)、常见算法 进入 深度学习——卷积神…...

微服务架构面试内容整理-API 网关-Gateway
Spring Cloud Gateway 是一个用于构建 API 网关的框架,它为微服务架构提供了灵活的路由和过滤功能。作为 Spring Cloud 生态的一部分,Gateway 提供了易于使用的 API 和强大的功能,适合用于现代微服务架构中的请求管理和服务交互。以下是 Spring Cloud Gateway 的主要特点、工…...

22.04Ubuntu---ROS2使用rclcpp编写节点C++
节点需要存在于功能包当中,功能包需要存在于工作空间当中。 所以我们要想创建节点,就要先创建一个工作空间,再创建功能包。 第一步:创建工作空间 mkdir -p chapt2_ws/src/ 第二步:创建example_cpp功能包,…...

XML 现实案例:深入解析与应用
XML 现实案例:深入解析与应用 XML(可扩展标记语言)自1998年成为W3C推荐标准以来,一直是数据交换和存储的重要工具。它是一种用于标记电子文件的结构化语言,使得数据不仅人类可读,而且机器可处理。本文将探讨XML在现实世界中的应用案例,展示其如何在不同领域中发挥作用。…...

Spring源码(十二):Spring MVC之Spring Boot
本篇将详细讨论Spring Boot 的启动/加载、处理请求的具体流程。我们先从一个简单的Spring Boot项目日志开始分析(这里假设读者已经仔细阅读完了前面的文章,且对Spring源码有一定深度的了解,否则会看得一脸懵逼)。 本文为2024重置…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
