【C语言】。末尼
用js写一个冒泡排序
当然可以。在JavaScript中,你可以使用递归的方式来实现冒泡排序算法。这是一个简单的示例:
function bubbleSort(arr) {
let len = arr.length;
if(len <= 1){
return arr; // 如果数组只有一个元素或为空,直接返回
}
// 从第一个元素开始遍历到倒数第二个
for(let i = 0; i < len - 1; i++){
// 如果当前元素大于下一个元素,则交换它们的位置
if(arr[i] > arr[i + 1]){
[arr[i], arr[i + 1]] = [arr[i + 1], arr[i]]; // 使用数组解构赋值进行交换
}
}
// 递归处理剩下的元素
return bubbleSort(arr.slice(0, len - 1)).concat(arr[len - 1]);
}
// 测试冒泡排序
let numbers = [64, 34, 25, 12, 22, 11, 90];
console.log("Sorted array:", bubbleSort(numbers));
冒泡排序的时间复杂度是多少?
冒泡排序的时间复杂度主要取决于数组的原始状态。在最好的情况下,即输入数组已经是完全有序的情况下,冒泡排序只需要遍历一次数组,时间复杂度为 O(n),其中 n 是数组长度。
然而,在最坏的情况,即输入数组是逆序排列的,每一轮比较都需要交换 n-1 次,总共需要进行 n 轮这样的操作,因此时间复杂度是 O(n^2)。这是因为冒泡排序每次都会考虑相邻的两个元素并可能交换位置,所以随着数组长度的增长,其效率会急剧下降。
冒泡排序的空间复杂度是多少?
冒泡排序的空间复杂度是O(1),因为它只需要一个额外的常数空间用于存储临时变量,无论输入数组的大小如何变化,需要的额外空间都是固定的。冒泡排序算法通过交换相邻元素来逐步把较大的元素“浮”到数组的顶部,过程中不需要额外的数据结构来辅助整个过程。所以,其空间效率非常高,是一种就地排序算法。


相关文章:

【C语言】。末尼
用js写一个冒泡排序 当然可以。在JavaScript中,你可以使用递归的方式来实现冒泡排序算法。这是一个简单的示例: function bubbleSort(arr) { let len arr.length; if(len < 1){ return arr; // 如果数组只有一个元素或为空…...

【鉴权】深入解析 Token:身份认证的核心技术
目录 引言一、Token 的定义与概念1.1 Token 是什么?1.2 无状态性与自包含性1.3 Token 的工作流程1.3.1 基本工作流程1.3.2 工作流程图示 二、Token 的常见用途2.1 用户身份验证2.2 授权控制2.3 防止跨站请求伪造(CSRF)2.4 跨域认证 三、Token…...
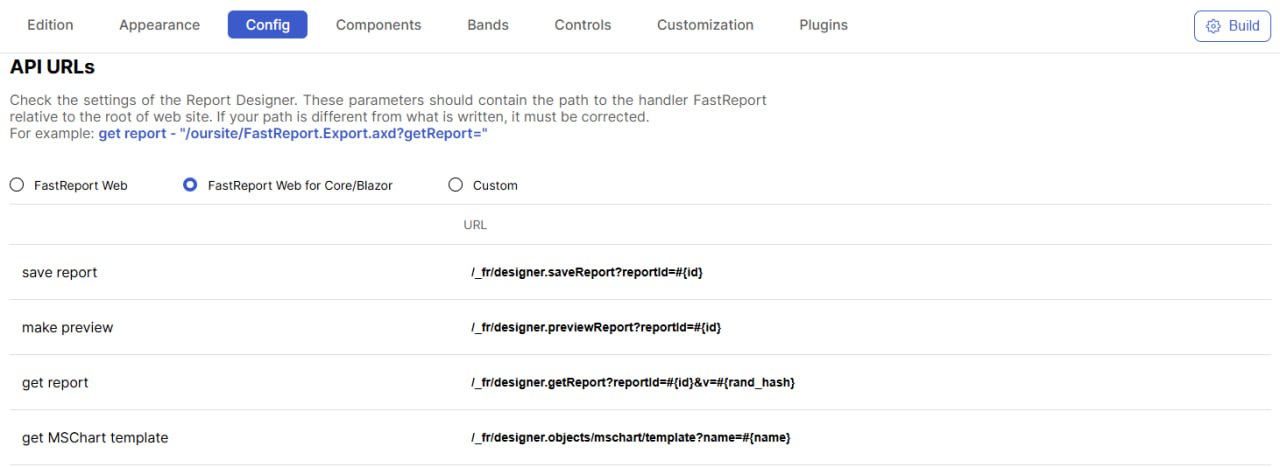
FastReport将停止 .NET Framework 上的 WebReport 更新
从2024/ 12 /1 日起,Fastreport将停止发布更新和提供对 FastReport.Web (.NET Framework) 的技术支持。该库一直是使用 Online Designer 的许多项目中报告的核心。这些更改意味着 FastReport.Web (Legacy) 库(FastReport.Net包的一部分)将不再…...

面试:TCP、UDP如何解决丢包问题
文章目录 一、TCP丢包原因、解决办法1.1 TCP为什么会丢包1.2 TCP传输协议如何解决丢包问题1.3 其他丢包情况(拓展)1.4 补充1.4.1 TCP端口号1.4.2 多个TCP请求的逻辑1.4.3 处理大量TCP连接请求的方法1.4.4 总结 二、UDP丢包2.1 UDP协议2.1.1 UDP简介2.1.2…...

在Ubuntu下安装RabbitMQ、添加一个新的登录用户并设置密码
在Ubuntu下安装RabbitMQ、添加一个新的登录用户并设置密码 在Ubuntu下安装RabbitMQ可以按照以下步骤进行:步骤 1: 更新系统步骤 2: 安装Erlang步骤 3: 添加RabbitMQ仓库步骤 4: 更新APT索引并安装RabbitMQ步骤 5: 启动RabbitMQ服务步骤 6: 检查RabbitMQ状态步骤 7: …...

HTTPS通信和TCP通信有什么不一样
HTTPS通信和TCP通信的主要区别如下: 协议层次:HTTPS是应用层协议,建立在HTTP协议之上,并增加了SSL/TLS加密层;而TCP是传输层协议,提供可靠的数据传输服务。安全性:HTTPS通过SSL/TLS加密…...

Kafka 的一些问题,夺命15连问
kafka-中的组成员 kafka四大核心 生产者API 允许应用程序发布记录流至一个或者多个kafka的主题(topics)。 消费者API 允许应用程序订阅一个或者多个主题,并处理这些主题接收到的记录流 StreamsAPI 允许应用程序充当流处理器(s…...

unity3d————延时函数
1.public void InvokeRepeating(string methodName, float time, float repeatRate); 延迟重复执行函数 InvokeRepeating 参数一:函数名字符串 参数二:第一次执行的延迟时间 参数三:之后每次执行的间隔时间 注意: 1-1.延时函数第…...

计算机学生自我提升方法——善用搜索引擎
计算机学生自我提升方法——善用搜索引擎 在信息爆炸的时代,计算机专业的学生如何有效地自我提升?答案可能就藏在一个简单却强大的工具——搜索引擎中。搜索引擎不仅是获取知识的入口,更是解决问题的利器。下面,我将分享一些善用…...

游戏引擎学习第一天
视频参考: https://www.bilibili.com/video/BV1zGDCYHErA/ 创建一个保存项目的路径 VS的安装略过,个人自行百度 1. vs 创建第一个CMAKE的窗口项目 game.cpp 修改如下的代码 到https://learn.microsoft.com/en-us/windows/win32/api/winbase/nf-winbase-winmain 去…...

uni-app view循环绑定click和 v-if
<view class"layout-wrap-item" v-for"(item, index) in menuItems" :key"index" click"item.clickHandler" :v-if"showMenu(item)"></view> const xxx (id) > { }; // 定义菜单项数组 const menuItems …...

Redis 高并发分布式锁实战
目录 环境准备 一 . Redis 安装 二:Spring boot 项目准备 三:nginx 安装 四:Jmeter 下载和配置 案例实战 优化一:加 synchronized 锁 优化二:使用 redis 的 setnx 实现分布式锁 优化三:使用 Lua 脚本…...

关于elementui el-radio 赋值问题
今天遇到这样的问题: 点击的时候,同时选中 照抄官网! 后来发现了问题: 也就是说如果你的版本太低,就不能用value,而得用label,于是修改 <el-radio-group v-model"searchTime"&g…...

2024-11-6----Android 11(全志713m)----- 关于添加 Selinux 权限
需求 节点: /sys/devices/platform/motor0/motor_ctrl上层 APP 使用 JNI 需要对该节点进行 echo 的操作,操作失败。 添加前的验证工作 adb 进去验证下,如下图所示: 发现权限不够。su 以后再操作是OK的,如下图: 添加前的修改 为防止报权限错误,直接给777,因为该…...
)
shodan5(泷羽sec)
声明 学习视频来自B站UP主 泷羽sec,如涉及侵泷羽sec权马上删除文章。 笔记只是方便各位师傅学习知识,以下网站只涉及学习内容,其他的都与本人无关,切莫逾越法律红线,否则后果自负 这节课旨在扩大自己在网络安全方面的知识面,了解网络安全领域的见闻,了…...

【Linux】Ansible集中化运维工具(详解)安装、常用模块、playbook脚本
文章目录 一、Ansible安装及远程控制1、关闭防火墙和SELinux2、安装ansible3、配置SSH无密码登录1、在管理机上生成一对密钥2、将公钥下发到远程主机3、保管密钥 4、主机目录 二、常用模块1、setup模块2、copy模块3、file模块4、shell模块5、script模块6、ping模块7、group模块…...

惠州石湾DELL T130服务器黄灯不开机案例
惠州石湾一个朋友反馈一台DELL PowerEdge T130 塔式服务器故障为 通电后无法开机,前面同时亮3个故障灯。闪电灯,电压灯,高温灯 1:这种情况建议大家更换一个同型号的电源进行故障排除。 2:朋友把该服务器硬件最小化测…...

⭐SmartControl: Enhancing ControlNet for Handling Rough Visual Conditions
目录 0 Abstract 1 Motivation 2 Related Work 2.1 Text-to-Image Diffusion Model 2.2 Controllable Text-to-Image Generation 2.3 ControlNet 2.4 Control Scale Exploration 3 Method 3.1 Framework 3.2 Control Scale Predictor 3.3 Unaligned Data Constructi…...

wordpress站外调用指定ID分类下的推荐内容
在WordPress中,如果你想从站外调用指定ID分类下的推荐内容,你可以使用WordPress REST API来实现。以下是一个基本的步骤指南: 1. 启用REST API 确保你的WordPress站点已经启用了REST API。大多数现代WordPress版本默认启用此功能。 2. 获取…...

Ente: 我们的 Monorepo 经验
原文:manav - 2024.10.29 九个月前,我们切换到了 monorepo。在此,我将介绍我们迄今为止的切换经验。 这并不是一份规范性的建议,而是一个经验的分享,目的是希望能够帮助其他团队做出明智的决策。 与大多数岔路不同&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
