洛谷 P1725 琪露诺(线段树优化dp)
题目链接
https://www.luogu.com.cn/problem/P1725
思路
我们令 d p [ i ] dp[i] dp[i]表示琪露诺移动到第 i i i个格子时能够获得的最大冰冻指数。
显然,状态转移方程为: d p [ i ] = m a x ( d p [ i ] , d p [ k ] + a [ i ] ) dp[i] = max(dp[i],dp[k]+a[i]) dp[i]=max(dp[i],dp[k]+a[i]),其中 k + L ≤ i k+L \le i k+L≤i并且 ( k + R ≥ i ) (k+R \ge i) (k+R≥i)。
因为 L L L和 R R R的值很大,所以我们可以使用线段树来进行优化。
使用线段树维护区间 d p [ i ] dp[i] dp[i]的最大值,每计算出一个新的 d p [ i ] dp[i] dp[i],就将其扔到线段树中。我们令编号从 1 1 1开头,则最后的答案为 d p [ n + 2 ] dp[n+2] dp[n+2]。
代码
#include <bits/stdc++.h>using namespace std;#define int long long
#define double long doubletypedef long long i64;
typedef unsigned long long u64;
typedef pair<int, int> pii;const int N = 2e5 + 5, M = 1e6 + 5;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f3f3f3f3f;int n, l, r;
int a[N], dp[N];
struct segmenttree
{struct node{int l, r, maxx, tag;};vector<node>tree;segmenttree(): tree(1) {}segmenttree(int n): tree(n * 4 + 1) {}void pushup(int u){auto &root = tree[u], &left = tree[u << 1], &right = tree[u << 1 | 1];root.maxx = max(left.maxx, right.maxx);}void pushdown(int u){auto &root = tree[u], &left = tree[u << 1], &right = tree[u << 1 | 1];if (root.tag){left.tag = root.tag;right.tag = root.tag;left.maxx = root.tag;right.maxx = root.tag;root.tag = 0;}}void build(int u, int l, int r){auto &root = tree[u];root = {l, r};if (l == r){root.maxx = -inf;return;}int mid = l + r >> 1;build(u << 1, l, mid);build(u << 1 | 1, mid + 1, r);pushup(u);}void modify(int u, int l, int r, int val){auto &root = tree[u];if (root.l >= l && root.r <= r){root.maxx = val;root.tag = val;return;}pushdown(u);int mid = root.l + root.r >> 1;if (l <= mid) modify(u << 1, l, r, val);if (r > mid) modify(u << 1 | 1, l, r, val);pushup(u);}int query(int u, int l, int r){auto &root = tree[u];if (root.l >= l && root.r <= r){return root.maxx;}pushdown(u);int mid = root.l + root.r >> 1;int res = -inf;if (l <= mid) res = query(u << 1, l, r);if (r > mid) res = max(res, query(u << 1 | 1, l, r));return res;}
};
void solve()
{cin >> n >> l >> r;fill(dp, dp + 1 + n + 2, -inf);for (int i = 1; i <= n + 1; i++){cin >> a[i];}segmenttree smt(n + 1);smt.build(1, 1, n + 1);dp[1] = a[1];smt.modify(1, 1, 1, dp[1]);for (int i = 2; i <= n + 1; i++){if (i - l < 1){dp[i] = -inf;continue;}dp[i] = max(dp[i], smt.query(1, max(i - r, 1ll), max(i - l, 1ll)) + a[i]);smt.modify(1, i, i, dp[i]);}//n+2表示对岸,包括>n+1的所有格子,所以要特殊处理。dp[n + 2] = smt.query(1, max(n + 2 - r, 1ll), max(n + 2 - 1, 1ll));cout << dp[n + 2] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int test = 1;// cin >> test;for (int i = 1; i <= test; i++){solve();}return 0;
}
相关文章:
)
洛谷 P1725 琪露诺(线段树优化dp)
题目链接 https://www.luogu.com.cn/problem/P1725 思路 我们令 d p [ i ] dp[i] dp[i]表示琪露诺移动到第 i i i个格子时能够获得的最大冰冻指数。 显然,状态转移方程为: d p [ i ] m a x ( d p [ i ] , d p [ k ] a [ i ] ) dp[i] max(dp[i],dp…...

【LeetCode】【算法】19. 删除链表的倒数第N个结点
LeetCode 19. 删除链表的倒数第N个结点 题目描述 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 思路 思路:快慢指针,快指针先移动n步,快慢指针再同时移动直到快指针到达链表末尾,此…...

Python爬虫 | 爬取豆瓣电影Top250的数据
简单记录一下,实现爬取豆瓣电影Top 250的数据。 这里我使用requests库来发送HTTP请求,以及BeautifulSoup库来解析HTML页面。 1.安装requests和BeautifulSoup库。 如果没有安装,可以通过以下命令安装: pip install requests bea…...

mac 中python 安装mysqlclient 出现 ld: library ‘ssl‘ not found错误
1. 出现报错 2. 获取openssl位置 brew info openssl 3. 配置环境变量(我的是在~/.bash.profile) export LDFLAGS"-L/opt/homebrew/Cellar/openssl3/3.4.0/lib" export CPPFLAGS"-I/opt/homebrew/Cellar/openssl3/…...

完全清除:苹果手机照片怎么彻底删除
在使用iPhone的过程中,由于拍摄积累的照片往往会占用大量存储空间。有时候,我们需要彻底删除这些照片以释放空间或保护隐私。苹果手机照片怎么彻底删除?在此,本文将与你分享一些实用的技巧。 彻底删除的重要性 彻底删除照片不仅涉…...

高德地图多个图片组成标点(自定义点标记内容)
图标的实现自定义点标记内容...

02-1_MVCC版本链清理
MVCC-版本链清理 文章目录 MVCC-版本链清理简介依赖机制Purge 操作的触发时机版本链清理的详细过程示例操作流程延迟清理配置和监控总结 简介 MySQL 中的 MVCC 机制通过版本链来管理数据的多版本存储,以支持高并发的读写操作。然而,随着事务的进行&…...

探索Python视频处理的瑞士军刀:ffmpeg-python库
文章目录 **探索Python视频处理的瑞士军刀:ffmpeg-python库**第一部分:背景介绍第二部分:ffmpeg-python库是什么?第三部分:如何安装ffmpeg-python库?第四部分:简单库函数使用方法1. 视频转码2. …...

进程间通信 - 通道
进程间通信 - 通道 什么是管道? 进程间的通信方式有五种,分别为:管道、信号量、共享内存、消息队列和套接字。 管道:本质上就是一个文件,前面的进程以写方式打开文件,后面的进程以读方式打开。这样前面写完后面读,于…...

华为数通HCIA系列第5次考试-【2024-46周-周一】
文章目录 1、子网掩码有什么作用,和IP地址是什么关系,利用子网掩码可以获取哪些信息?2、已知一个IP地址是192.168.1.1,子网掩码是255.255.255.0,求其网络地址3、已知某主机的IP地址是192.168.100.200,子网掩…...

【Linux】如何通过终端命令查看当前可用网络 WIFI + 设置已配置网络的连接优先级 + 连接/断连网络
【Linux】通过命令行,查看当前可用网络 WIFI 设置已配置网络的连接优先级 连接网络 列出所有可连接网络 nmcli device wifi list这个命令会列出所有可连接 wifi,*表示当前连接。 IN-USE BSSID SSID MODE CHAN …...

华为路由策略配置
一、AS_Path过滤 要求: AR1与AR2、AR2与AR3之间建立EBGP连接 AS10的设备和AS30的设备无法相互通信 1.启动设备 2.配置IP地址 3.配置路由器的EBGP对等体连接,引入直连路由 [AR1]bgp 10 [AR1-bgp]router-id 1.1.1.1 [AR1-bgp]peer 200.1.2.2 as-nu…...

Debezium日常分享系列之:异步 Debezium 嵌入式引擎
Debezium日常分享系列之:异步 Debezium 嵌入式引擎 动机目标非目标保留Kafka Connect模型计划的更改线程池并行运行源任务存储偏移量并发处理CDC事件禁用CDC事件的完全排序自定义记录处理器并行处理记录的选项存储偏移量引擎状态和生命周期防止资源泄漏异常处理退出…...

leetcode206. Reverse Linked List
Given the head of a singly linked list, reverse the list, and return the reversed list. 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 思路一:双指针 class Solu…...

【MATLAB源码-第291期】基于matlab的AMI编码解码系统仿真,输出各个节点波形。
操作环境: MATLAB 2022a 1、算法描述 AMI(Alternate Mark Inversion,交替极性反转)是一种广泛使用的编码方法,尤其是在通信系统中,用于传输二进制数据。AMI编码的特点是在传输过程中,对于0信…...

springboot苍穹外卖实战:十一:复盘总结
近期在整理草稿区,故放出此贴。 server模块需要导入对common模块的依赖 <dependency><groupId>org.example</groupId><artifactId>sky-common</artifactId><version>1.0-SNAPSHOT</version></dependency>我现在有个…...

基于Python的药房管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

chat2db数据库图形化工具
数据库图形化工具 DataGrip:由 JetBrains 公司开发,是开发者中广为人知的数据库管理工具,功能强大且支持多种数据库。DBeaver:一款开源的数据库管理工具,虽然相对 DataGrip 知名度稍低,但在开发者社区中也…...
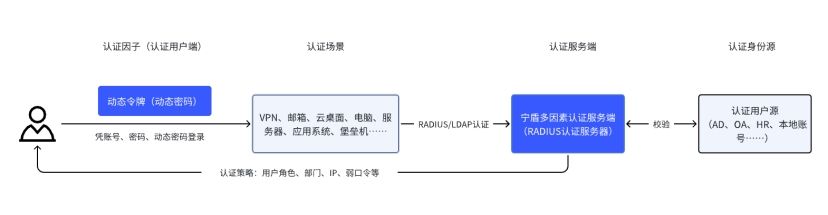
弱口令整改方案:借助双因子认证加强账号密码安全
弱口令整改方案可借助宁盾 2FA双因子身份认证来解决。双因子认证(也称双因素身份认证)是一种安全认证机制,通过结合两个及以上不同的身份验证因子,提高企业用户在办公、研发、生产、运维场景下的的账号密码安全性。它可以有效防止…...

动态代理的优势是什么?
在数据采集的世界里,效率和稳定性是衡量代理IP服务优劣的关键指标。动态代理,作为一种高效的网络工具,正逐渐成为企业和开发者的首选。今天,我们就来聊聊动态代理的优势,以及它如何成为数据采集的高效之选。 动态代理…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
