第十五届蓝桥杯JAVA的B组题目详情解析
(第一个填空太简单,就不写了,根本不用代码,直接excel计算)
目录
蓝桥杯第二个填空,类斐波那契循环数
蓝桥杯JAVA.b组第三题 -分布式队列(模拟)
食堂(蓝桥杯D题)
编辑
星际旅行(Floyd佛洛依德)
其余的有点变态,感觉学了好像也没用,还是算了
蓝桥杯第二个填空,类斐波那契循环数

首先难点就是这个题目需要读懂,当初我就是没读明白,才没写出来,我一般都是写力扣的题,力扣的题更加偏向于方法,或者说是业务上的,而蓝桥杯更偏向那种数学的类型
这个难点是弄懂那个求和符号,我好久没学,都忘了
比如说9999999这个是7位数,然后假如我们写第10位,就是
public static void main(String[]args) {for(int i=10000000;i>=0;i--){char[] a=(i+"").toCharArray();int sum=0;int[]b=new int[a.length];for(int j=0;j<a.length;j++){b[j]=Integer.valueOf(a[j]+"");sum+=b[j];}while(true) {if (sum == i) {System.out.println(sum);return;} else if (sum > i) {break;}int tmp=sum;sum = 2 * sum - b[0];for (int j = 0; j < a.length - 1; j++) {b[j] = b[j + 1];}//更新最后一个值b[a.length - 1] = tmp;//处理前一个值,进行迭代处理}}
蓝桥杯JAVA.b组第三题 -分布式队列(模拟)
 这个代码是我觉得看的最清晰的一个,而且他的想法很简洁,适合我这种菜鸡
这个代码是我觉得看的最清晰的一个,而且他的想法很简洁,适合我这种菜鸡
这个题难度就是你选择的问题,你假如选择不正好的策略,会麻烦好多。像是我开始想用数组,因为下标不好表示,(开始我也是寻思用集合,但是困在一些问题上,选择自己更擅长的,但是确没想到更麻烦,而且没解出来)
public static void main(String[]args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();//使用一个类似二维数组List<List<Integer>> nums=new ArrayList<>();for(int i=0;i<n;i++){//这个数组有添加n个队列nums.add(new ArrayList<>());}while (sc.hasNext()) {//通过command判断输入的例子。String command = sc.next();if (command.equals("add")) {int num=sc.nextInt();//假如此时需要添加元素,则需要在第一个集合里面添加元素nums.get(0).add(num);} else if (command.equals("sync")) {//获取到我们需要添加到哪号队列int seq = sc.nextInt();//nums获取到这个队列,假如里面的个数小于一号队列个数if(nums.get(seq).size()<nums.get(0).size()) {//nums的seq队列添加队列0里面的获取的是队列2的长度,队列2的下标永远是没到这个位置,所以需要到2号这个下标nums.get(seq).add(nums.get(0).get(nums.get(seq).size()));}} else {//找到n个队列中到元素个数int min_count = Integer.MAX_VALUE;for (int i = 0; i < n; i++) {//获取到每个元素,然后min代表最后的元素,模拟(很牛逼的思路,第二个)if (nums.get(i).size() < min_count) min_count = nums.get(i).size();}System.out.println(min_count);}}}食堂(蓝桥杯D题)
这个题看着就恶心的模拟,但是假如说暴力穷举肯定也是可以,但是缺点是什么呢?
缺点就是她这个你很容易有想不到的情况,而且这些情况加一起,的顺序性就很恶心
所以相比较之下,还是下面这个方法更好
这道题我相信大部分人的思路肯定是从食堂桌子出发,那么我们需要做的就是分解他条件的思考
首先4个桌子,6个桌子,我们肯定是第一时间,先凑出来6人桌子,2个三人桌肯定是最优先,然后我们考虑的是什么,2+4肯定6个,2+2+2肯定6个,但是假如换个思路,假如已经坐了两个人,我们是不是可以默认这个食堂多了一个四人桌子,如果这么考虑,我们很多情况都可以合并到一起,只需要考虑四人桌子就行,
四人桌子肯定还是优先4人和2个2人,假如这些都完事了,说明什么情况呢,
存在六人桌子,存在4人和3人,但是不存在2人
存在4人桌子,可能存在两个人,可能存在三个人,(有人可能问我们在开始就判断了是否可能出现2个人,结果是一定不会有两个人,但是假如没有六人桌子的情况下,是否有可能出现2个人呢,也是有可能的)
这些情况综合起来只有一句话,就是一个桌子只能坐一个寝室,你2人,3人,4人都好
我只要把最后的桌子都放到一起,然后4人就给一个桌子(不管它是4人还是6人,反正一定能装下)
(这里补充:可能你觉得不靠谱,去试试假如5个人咋整,(5个人的前提是有2个人,2个人要么我存在6人桌子被分开,要不存在六个人的桌子,那样坐不了五个人,所以还是一个桌子一个寝室)
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {public static void main(String[]args) {Scanner scan = new Scanner(System.in);int q=scan.nextInt();int[][]a=new int[q][5];//选择的角度应该是从桌子入手,//a[0][0]:两人寝室,[1]三人寝室,[2]四人寝室 [3]四个人桌子[4]六人桌子//更优秀的思想,把六个人的桌子转化为四个人的桌子for(int i=0;i<q;i++){for(int j=0;j<5;j++){a[i][j]=scan.nextInt();}int count=0;//a[0][0]:两人寝室,[1]三人寝室,[2]四人寝室 [3]四个人桌子[4]六人桌子//假如有六人桌子优先分配2个三人while(a[i][4]>0&&a[i][1]>=2){a[i][1]-=2;a[i][4]--;count+=6;}//假如有六人桌子优先分配1个两人,这样,就相当于多了一个四个人的桌子while(a[i][4]>0&&a[i][0]>0){a[i][4]--;a[i][0]--;a[i][3]++;//相当于多了一个四人桌子count+=2;}//假如四人桌子优先分配四个人的while(a[i][3]>0&&a[i][2]>0){a[i][2]--;a[i][3]--;count+=4;}//四人寝室没了,四人桌子优先给2个2人寝室while(a[i][3]>0&&a[i][0]>=2){//2人寝室则剪去2个a[i][0]-=2;a[i][3]--;count+=4;}//到了最后其实就都不是凑整数的情况,换句话说,咋吗都坐不满,6人能转化的,都转化了,转化不了的,也同化成4个人//因为假如你想5个人是3+2,相当于四人寝室住了3个人,换句话,最后四人桌子还是六人桌子已经没有区别了int num=a[i][4]+a[i][3];//以下的情况都是满足不了的while(num>0&&a[i][2]>0){num--;a[i][2]--;count+=4;}while(num>0&&a[i][1]>0){num--;a[i][1]--;count+=3;}while(num>0&&a[i][0]>0){num--;a[i][0]--;count+=2;}System.out.println(count);}scan.close();}}最优分组(数学题)


星际旅行(Floyd佛洛依德)

static int n,m,q;static int[][] con;public static void main(String[] args) {Scanner zh=new Scanner(System.in);n=zh.nextInt();m=zh.nextInt();q=zh.nextInt();con=new int[n+1][n+1];//我们选择从[1-n]闭区间,不考虑0
//处理边界值比如0x之类的for(int i=1;i<=n;i++)Arrays.fill(con[i], 3010);for(int i=1;i<=n;i++)con[i][i]=0;for(int i=0;i<m;i++) {int a=zh.nextInt();int b=zh.nextInt();con[a][b]=1;con[b][a]=1;}//算法核心,核心问题也在这里k在最外面和k在循环的最里面有什么区别for(int k=1;k<=n;k++) {for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) {
//这个的核心是类似于动态规划从con[i][j],con[i][k]+[k][j],从i到j,需要i通过k到j
//相当于算从i到j位置的最短路径,con[i][j]=Math.min(con[i][j], con[i][k]+con[k][j]);}}}int ans=0;for(int i=0;i<q;i++) {int x=zh.nextInt();int y=zh.nextInt();int count=0;
//我们从x点出发,到达j点花费步骤假如小于y就说明可以到达,count++;for(int j=1;j<=n;j++)if(con[x][j]<=y)count++;//System.out.println(count);ans+=count;}System.out.printf("%.2f", (double)ans/q);}其余的有点变态,感觉学了好像也没用,还是算了
相关文章:

第十五届蓝桥杯JAVA的B组题目详情解析
(第一个填空太简单,就不写了,根本不用代码,直接excel计算) 目录 蓝桥杯第二个填空,类斐波那契循环数 蓝桥杯JAVA.b组第三题 -分布式队列(模拟) 食堂(蓝桥杯D题) 编辑 星际旅行(Floyd佛洛依德) 其余的有点变态,感觉学了好像…...

在几分钟内将数据从 Oracle 迁移到 ClickHouse
ClickHouse 是一个开源的面向列的数据库管理系统。它在实时数据处理方面的出色性能显着增强了数据分析和业务洞察力。将数据从 Oracle 迁移到 ClickHouse 可以释放数据在决策中的力量,这是单独使用 Oracle 无法实现的。 本教程介绍如何使用 BladePipe 将数据从 Orac…...

ASP.NET MVC宠物商城系统
该系统采用B/S架构,使用C#编程语言进行开发,以ASP.NET MVC框架为基础,以Visual Studio 2019为开发工具,数据库采用SQL Server进行保存数据。系统主要功能包括登录注册、宠物展示、个人中心、我的订单、购物车、用户管理、宠物类别…...

完整http服务器
目录 背景目标描述技术特点开发环境WWW客户端浏览发展史服务端http发展史http分层概览 背景 http协议被广泛使用,从移动端,pc浏览器,http无疑是打开互联网应用窗口的重要协议,http在网络应用层中的地位不可撼动,是能…...
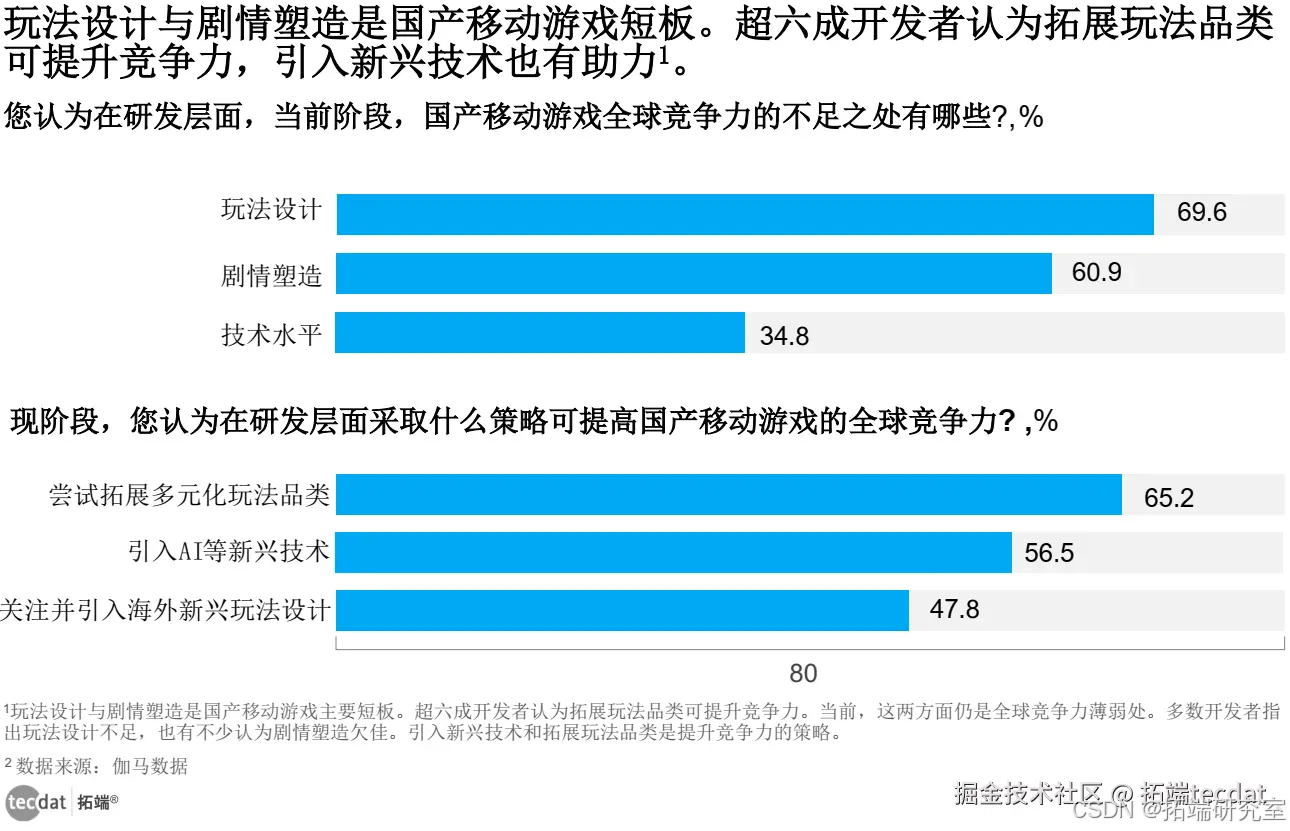
【专题】2024AIGC创新应用洞察报告汇总PDF洞察(附原数据表)
原文链接:https://tecdat.cn/?p38310 在科技日新月异的今天,人工智能领域正以前所未有的速度发展,AIGC(人工智能生成内容)成为其中最耀眼的明珠。从其应用场景的不断拓展,到对各行业的深刻变革࿰…...
形态学图像处理(Morphological Image Processing)
形态学图像处理(Morphological Image Processing) 前言 本博客为个人总结数字图像处理一课所写,并给出适当的扩展和相应的demo。 写博客跟做 checkpoint 很像,毕竟个人还不能达到那种信手拈来的境界,忘了就是从零开始训练࿰…...

【IDER、PyCharm】免费AI编程工具完整教程:ChatGPT Free - Support Key call AI GPT-o1 Claude3.5
文章目录 CodeMoss 简介CodeMoss 的模型集成如何安装和配置 CodeMossIDER 插件安装步骤 CodeMoss 的实战使用AI 问答功能代码优化与解释优化这段代码解释这段代码 文件上传与对话联网查询与 GPT 助手联网查询GPT 助手 提升开发效率的最佳实践结语更多文献 CodeMoss 简介 CodeM…...

C++11的一些实用特性
1.统一的列表初始化 在C98中,标准允许使用花括号{}对数组或者结构体元素进行统一的列表初始值设定。 //统一的列表初始化 struct Date {int year;int month;int day; };void test1() {Date d1 { 2024,11,14 };int array1[] { 1, 2, 3, 4, 5 };int array2[5] { …...

23种设计模式-观察者(Observer)设计模式
文章目录 一.什么是观察者模式?二.观察者模式的结构三.观察者模式的应用场景四.观察者模式的优缺点五.观察者模式的实现(C示例)六.观察者模式的实现(JAVA示例)七.代码解释八.总结 类图: 观察者设计模式类图…...

【CUDA】Branch Divergence and Unrolling Loop
目录 一、避免分支发散 1.1 并行规约问题 1.2 并行规约中的发散 二、UNrolling Loops 一、避免分支发散 控制流有时依赖于 thread 索引。同一个warp中,一个条件分支可能导致性能很差。通过重新组织数据获取模式可以减少或避免 warp divergence。具体问题查看下…...

深度学习:卷积神经网络的计算复杂度,顺序操作,最大路径长度
卷积层的计算复杂度 在深度学习中,卷积层的计算复杂度主要取决于卷积核的大小、输入和输出的通道数量、以及输入序列的长度。具体来说,卷积层的计算复杂度可以通过以下几个因素来计算: 卷积核大小 k:卷积核的大小决定了每次卷积操…...

springboot 配置文件中 multipart.max-file-size 各个版本的写法
由于springboot具有几个版本,不同版本对于文件上传最大限制的配置也有所不同。 所以要注意springboot本身的版本,不然会一直报错 在springboot1.3版本中: multipart.maxFileSize在springboot1.4与springboot1.5版本中: spring…...

linux 中mysql查看慢日志
1、到mysql容器,先登录到数据库,查看是否开启 mysql -h 127.0.0.1 -uroot -p SHOW VARIABLES LIKE slow_query_log; 2、如果没有开启,需要先开启 set global slow_query_log ON; 3、查看慢日志文件 SHOW VARIABLES LIKE slow_query_log…...

单片机的基本组成与工作原理
单片机(Microcontroller Unit, MCU)是一种将计算机的主要部分集成在一个芯片上的小型计算机系统。它通常包括中央处理器(CPU)、存储器(Memory)、输入输出接口(I/O Ports)、定时器/计…...

智慧隧道和智慧交通
通过引入先进的物联网技术,将各种硬件设备如传感器、摄像头、控制系统等有效地连接并管理起来,以实现道路安全和交通流畅的目标。这些设备将能够实时监控和控制隧道内的各种设备和系统,从而提高道路安全、提升驾驶体验并降低管理成本。 在这个…...

List、Set、Map详解和区别
在 Java 中,List、Set、Map是常用的集合类型,它们各自具有不同的特点和用途,以下是对它们的详细介绍及区别分析: List(列表) 特点: 有序性:List中的元素是有序的,即元素…...
界面控件DevExpress WinForms v24.2新功能预览 - 支持.NET 9
DevExpress WinForms 拥有180组件和UI库,能为Windows Forms平台创建具有影响力的业务解决方案。DevExpress WinForms能完美构建流畅、美观且易于使用的应用程序,无论是Office风格的界面,还是分析处理大批量的业务数据,它都能轻松胜…...

Postman之pm.test断言操作
Postman之pm.test断言操作 1.断言方法2.连接符3.条件判断符 用于验证请求的响应数据是否符合预期 1.断言方法 pm.test():定义一个测试函数,接受两个参数,一个字符串参数用来描述该测试,一个返回True/False的函数 语法格式&#…...
对数几率回归
对数几率回归简介 对数几率回归(Logistic Regression)是一种用于解决分类问题的经典统计模型,其核心思想是利用逻辑函数(Sigmoid函数)将线性回归模型的输出值映射到概率范围 [0, 1],从而实现分类预测。对数…...

docker 配置同宿主机共同网段的IP 同时通过通网段的另一个电脑实现远程连接docker
docker配置网络 #宿主机执行命令 ifconfig 查询对应的主机ip 子网掩码 网关地址 #[网卡名称]:inet[主机IP] netmask[子网掩码] broadcast[网关地址]这里需要重点关注:eno1[网卡名称]以及【192.168.31.225】网关地址 在宿主机执行docker命令创建一个虚拟…...

StructBERT WebUI部署教程:容器化entrypoint.sh启动逻辑与容错机制解析
StructBERT WebUI部署教程:容器化entrypoint.sh启动逻辑与容错机制解析 1. 项目概述 StructBERT文本相似度服务是一个基于百度开源大模型的高精度中文句子相似度计算工具。这个WebUI应用能够帮助用户快速判断两个中文句子的语义相似程度,相似度评分范围…...
)
【漏洞赏金猎人必看】竞态条件漏洞:从概念到实战,一文讲透(含挖掘技巧)
【漏洞赏金猎人必看】竞态条件漏洞:从概念到实战,一文讲透(含挖掘技巧) 本文将带你从 0 到 1 彻底理解竞态条件漏洞,并学会在 SRC 和赏金平台中高效挖掘这类高价值漏洞。 我会用最通俗的方式,教你如何判断一…...

约束优化求解利器:从罚函数到乘子法的演进与实践
1. 约束优化:当你的目标遇到了“条条框框” 大家好,我是老张,在AI和算法这行摸爬滚打了十几年,今天想和大家聊聊一个听起来有点“硬核”,但实际上无处不在的技术话题——约束优化。咱们先别被名字吓到,我保…...

CCS编译报错:DSP2833x_Device.h文件缺失的排查与修复指南
1. 从“找不到头文件”说起:一个嵌入式新手的常见噩梦 如果你刚开始玩德州仪器(TI)的C2000系列DSP,尤其是经典的DSP28335、28334这些芯片,那你大概率绕不开一个开发环境:Code Composer Studio,也…...

Pendulum完全指南:10个技巧告别Python datetime的烦恼
Pendulum完全指南:10个技巧告别Python datetime的烦恼 【免费下载链接】pendulum Python datetimes made easy 项目地址: https://gitcode.com/gh_mirrors/pe/pendulum Pendulum是一个让Python datetime操作变得简单的强大库,它解决了原生datetim…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...


