【机器学习】机器学习中用到的高等数学知识-7.信息论 (Information Theory)
- 熵 (Entropy):用于评估信息的随机性,常用于决策树和聚类算法。
- 交叉熵 (Cross-Entropy):用于衡量两个概率分布之间的差异,在分类问题中常用。
信息论作为处理信息量和信息传输的数学理论,在机器学习中具有广泛的应用。本文将围绕熵(Entropy)和交叉熵(Cross-Entropy),探讨它们的定义、公式推导、应用场景及代码实现。
1. 熵 (Entropy)
1.1 定义
熵衡量信息的不确定性或随机性。它可以理解为“信息的平均量”,即某一分布下每个事件的信息量的期望值。
1.2 数学公式
对于一个离散随机变量 X,取值为 ,其熵定义为:
其中:
是事件
的概率;
- log 通常以 2 为底(信息量以比特为单位)或以 e 为底(信息量以 nat 为单位)。
1.3 推导过程
熵的来源可以从信息量(Information Content)定义出发:
熵是信息量的加权平均值,因而有:
1.4 应用场景
- 决策树算法:选择分裂点时使用熵减少量(信息增益)。
- 聚类算法:评估聚类后类别分布的随机性。
- 语言模型:评估文本序列的不确定性。
1.5 熵的Python代码实现
import numpy as np# 定义熵函数
def entropy(p):return -np.sum(p * np.log2(p))# 示例概率分布
p = np.array([0.5, 0.25, 0.25])
print("熵:", entropy(p))
熵: 1.51.6 图示
熵的图示展示了单一事件概率分布变化时的熵值变化。
import matplotlib.pyplot as plt
import numpy as npp = np.linspace(0.01, 0.99, 100)
entropy_values = -p * np.log2(p) - (1 - p) * np.log2(1 - p)plt.plot(p, entropy_values, label='Entropy')
plt.xlabel('P(x)')
plt.ylabel('H(X)')
plt.title('Entropy vs Probability')
plt.legend()
plt.grid()
plt.show()

2. 交叉熵 (Cross-Entropy)
2.1 定义
交叉熵用于衡量两个概率分布之间的差异。给定真实分布 P 和预测分布 Q,其定义为:
当 P 和 Q 相等时,交叉熵退化为熵。
2.2 推导过程
交叉熵的来源是 Kullback-Leibler (KL) 散度:
其中:
说明交叉熵包含了真实分布的熵和两分布之间的 KL 散度。
2.3 应用场景
- 分类问题:在机器学习中作为目标函数,尤其是多分类问题中的 Softmax 回归。
- 语言模型:衡量生成模型输出的分布与目标分布的匹配度。
- 聚类算法:评估聚类后的分布与目标分布的差异。
2.4 交叉熵的Python代码实现
import numpy as np# 定义交叉熵函数
def cross_entropy(p, q):return -np.sum(p * np.log2(q))# 示例真实分布和预测分布
p = np.array([1, 0, 0]) # 实际类别
q = np.array([0.7, 0.2, 0.1]) # 预测分布
print("交叉熵:", cross_entropy(p, q))
交叉熵: 0.51457317282975832.5 图示
交叉熵的图示对比了真实分布和不同预测分布间的差异。
import matplotlib.pyplot as plt
import numpy as npdef cross_entropy(p, q):return -np.sum(p * np.log2(q))p = np.array([1, 0, 0])
q_values = [np.array([0.7, 0.2, 0.1]), np.array([0.4, 0.4, 0.2])]ce_values = [cross_entropy(p, q) for q in q_values]
labels = ['Q1 (Closer)', 'Q2 (Further)']plt.bar(labels, ce_values, color=['blue', 'orange'])
plt.title('Cross-Entropy Comparison')
plt.ylabel('Cross-Entropy')
plt.show()
3. 实际案例:分类问题中的交叉熵
在图像分类中,交叉熵是常用的损失函数。对于一个三类分类问题:
- 真实类别为 [1, 0, 0]。
- 模型预测的概率分布为 [0.7, 0.2, 0.1]。
交叉熵计算结果为 0.514,比完全随机预测([1/3, 1/3, 1/3])的交叉熵小,表明模型预测效果更好。
总结
熵和交叉熵是信息论中的核心概念,其在机器学习中的重要性不可忽视。通过公式理解、代码实现和图示分析,我们可以更好地掌握这些工具,并有效地将其应用于实际问题中。
拓展阅读
【机器学习】数学知识:对数-CSDN博客
【机器学习】机器学习中用到的高等数学知识-2.概率论与统计 (Probability and Statistics)_机器学习概率-CSDN博客
相关文章:

【机器学习】机器学习中用到的高等数学知识-7.信息论 (Information Theory)
熵 (Entropy):用于评估信息的随机性,常用于决策树和聚类算法。交叉熵 (Cross-Entropy):用于衡量两个概率分布之间的差异,在分类问题中常用。 信息论作为处理信息量和信息传输的数学理论,在机器学习中具有广泛的应用。…...
《现代制造技术与装备》是什么级别的期刊?是正规期刊吗?能评职称吗?
问题解答 问:《现代制造技术与装备》是不是核心期刊? 答:不是,是知网收录的第二批认定学术期刊。 问:《现代制造技术与装备》级别? 答:省级。主管单位:齐鲁工业大学࿰…...

09 - Clickhouse的SQL操作
目录 1、Insert 1.1、标准 1.2、从表到表的插入 2、Update和Delete 2.1、删除操作 2.2、修改操作 3、查询操作 3.1、with rollup:从右至左去掉维度进行小计 3.2、with cube : 从右至左去掉维度进行小计,再从左至右去掉维度进行小计 3.3、with …...

如何解决pdf.js跨域从url动态加载pdf文档
摘要 当我们想用PDF.js从URL加载文档时,将会因遇到跨域问题而中断,且是因为会触发了PDF.js和浏览器的双重CORS block,这篇文章将会介绍:①如何禁用pdf.js的跨域?②如何绕过浏览器的CORS加载URL文件?②如何使…...
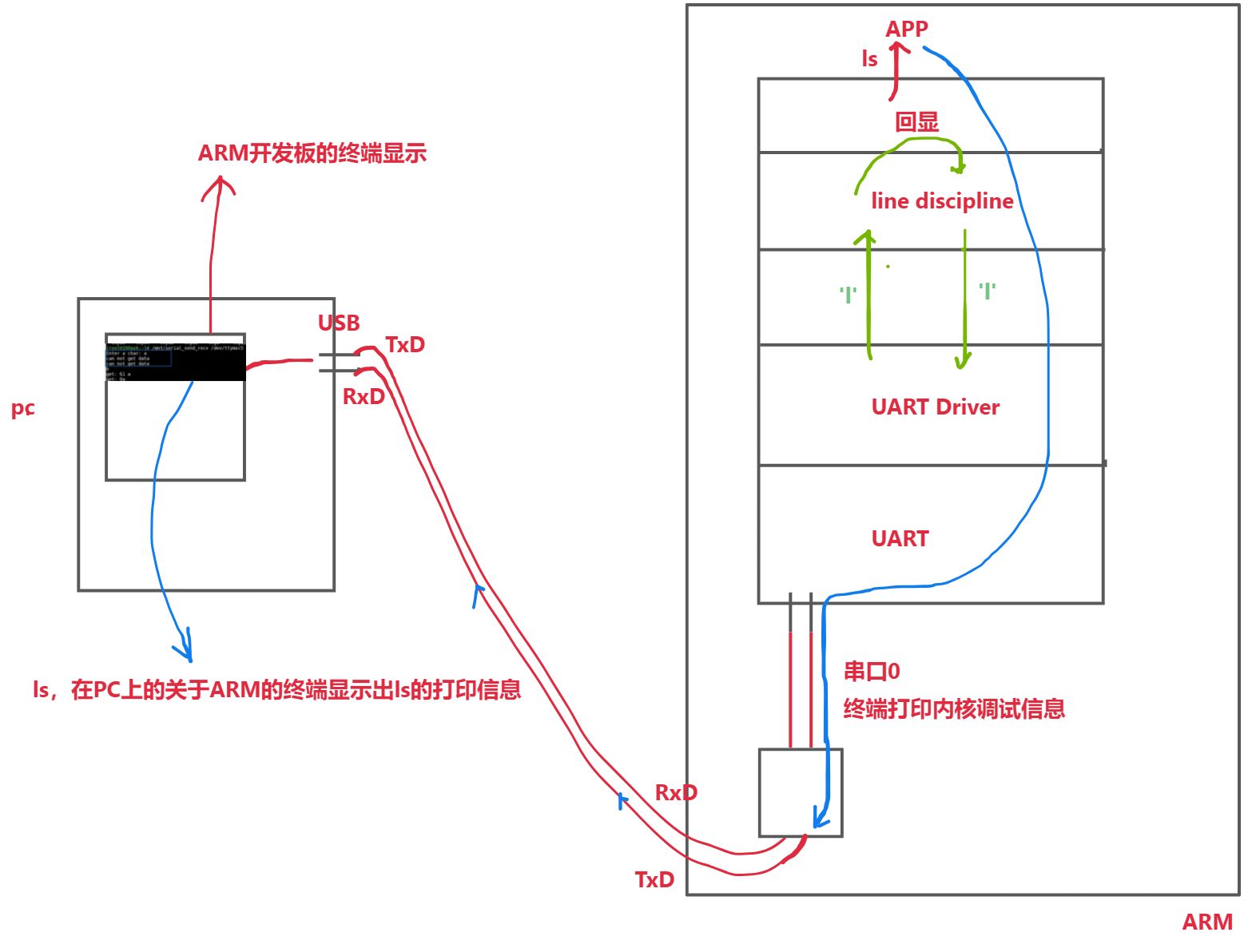
深入理解TTY体系:设备节点与驱动程序框架详解
往期内容 本专栏往期内容:Uart子系统 UART串口硬件介绍 interrupt子系统专栏: 专栏地址:interrupt子系统Linux 链式与层级中断控制器讲解:原理与驱动开发 – 末片,有专栏内容观看顺序 pinctrl和gpio子系统专栏…...
)
库的操作(MySQL)
1.创建数据库 语法: CREATE DATABASE [IF NOT EXISTS] db_name [create_specification [, create_specification] ...] create_specification:[DEFAULT] CHARACTER SET charset_name[DEFAULT] COLLATE collation_name说明: 大写的表示关键字 [ ] 是可…...

在 for 循环中,JVM可能会将 arr.length 提升到循环外部,仅计算一次。可能会将如何解释 详解
在 Java 的 for 循环中,JVM 有能力进行优化,将 arr.length 的访问提升到循环外部,避免每次迭代都重新计算 arr.length。这种优化主要是由于 JVM 的 即时编译器(JIT) 和 逃逸分析(Escape Analysis࿰…...

回溯--数据在内存中的存储:整数、大小端和浮点数的深度解析
目录 引言 1. 整数在内存中的存储 1.1 原码、反码和补码 1.2 为什么使用补码? 1.3 示例代码:整数的存储 2. 大小端字节序和字节序判断 2.1 什么是大端和小端? 2.2 为什么会有大端和小端之分? 2.3 字节序的判断小程序 2.…...

第二十二章 Spring之假如让你来写AOP——Target Object(目标对象)篇
Spring源码阅读目录 第一部分——IOC篇 第一章 Spring之最熟悉的陌生人——IOC 第二章 Spring之假如让你来写IOC容器——加载资源篇 第三章 Spring之假如让你来写IOC容器——解析配置文件篇 第四章 Spring之假如让你来写IOC容器——XML配置文件篇 第五章 Spring之假如让你来写…...

探索设计模式:原型模式
设计模式之原型模式 🧐1. 概念🎯2. 原型模式的作用📦3. 实现1. 定义原型接口2. 定义具体的原型类3. 定义客户端4. 结果 📰 4. 应用场景🔍5. 深拷贝和浅拷贝 在面向对象编程中,设计模式是一种通用的解决方案…...
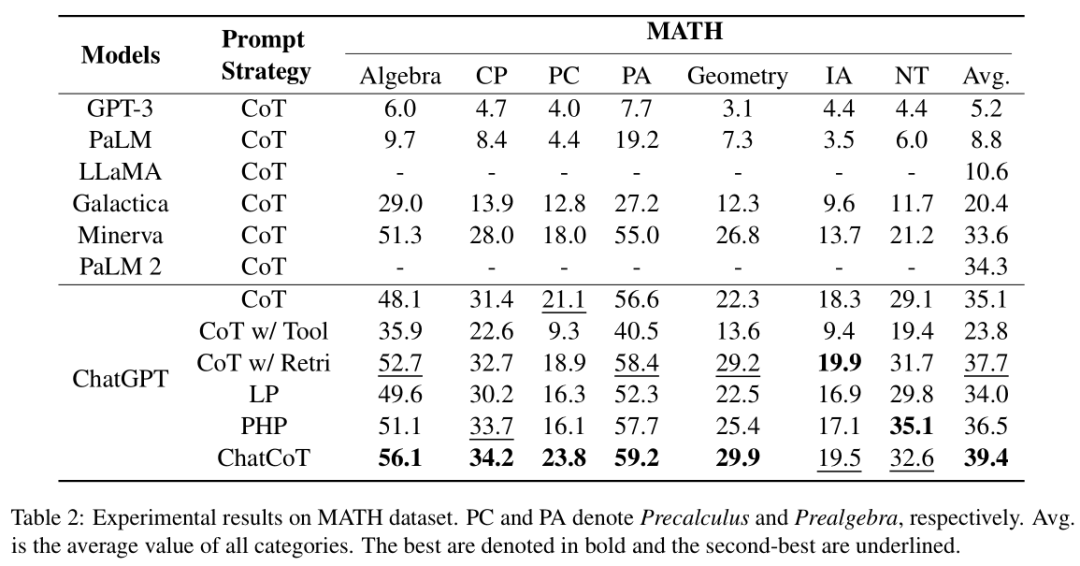
NLP论文速读(EMNLP 2023)|工具增强的思维链推理
论文速读|ChatCoT: Tool-Augmented Chain-of-Thought Reasoning on Chat-based Large Language Models 论文信息: 简介: 本文背景是关于大型语言模型(LLMs)在复杂推理任务中的表现。尽管LLMs在多种评估基准测试中取得了优异的成绩…...

JVM垃圾回收详解.②
空间分配担保 空间分配担保是为了确保在 Minor GC 之前老年代本身还有容纳新生代所有对象的剩余空间。 《深入理解 Java 虚拟机》第三章对于空间分配担保的描述如下: JDK 6 Update 24 之前,在发生 Minor GC 之前,虚拟机必须先检查老年代最大…...

什么是事务,事务有什么特性?
事务的四大特性(ACID) 原子性(Atomicity) 解释:原子性确保事务中的所有操作要么全部完成,要么全部不做。这意味着事务是一个不可分割的工作单元。在数据库中,这通常通过将事务的操作序列作为一个…...

深入解析:如何使用 PyTorch 的 SummaryWriter 进行深度学习训练数据的详细记录与可视化
深入解析:如何使用 PyTorch 的 SummaryWriter 进行深度学习训练数据的详细记录与可视化 为了更全面和详细地解释如何使用 PyTorch 的 SummaryWriter 进行模型训练数据的记录和可视化,我们可以从以下几个方面深入探讨: 初始化 SummaryWriter…...

企业微信中设置回调接口url以及验证 spring boot项目实现
官方文档: 接收消息与事件: 加密解密文档:加解密库下载与返回码 - 文档 - 企业微信开发者中心 下载java样例 加解密库下载与返回码 - 文档 - 企业微信开发者中心 将解压开的代码 ‘将文件夹:qq\weixin\mp\aes的代码作为工具拷…...

电脑超频是什么意思?超频的好处和坏处
嗨,亲爱的小伙伴!你是否曾经听说过电脑超频?在电脑爱好者的圈子里,这个词似乎非常熟悉,但对很多普通用户来说,它可能还是一个神秘而陌生的存在。 今天,我将带你揭开超频的神秘面纱,…...
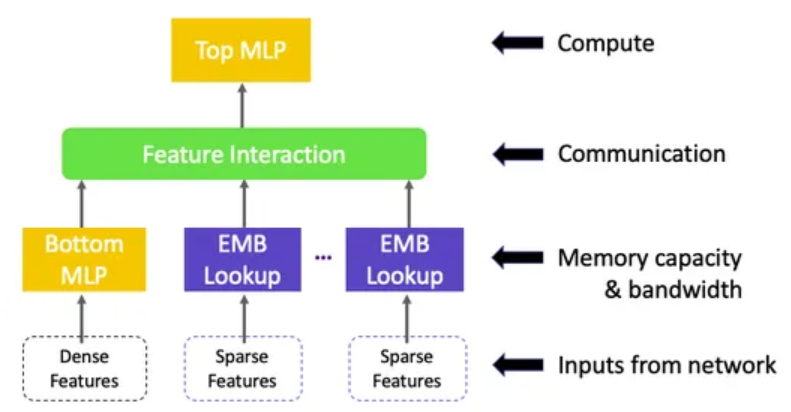
在 AMD GPU 上构建深度学习推荐模型
Deep Learning Recommendation Models on AMD GPUs — ROCm Blogs 2024 年 6 月 28 日 发布者 Phillip Dang 在这篇博客中,我们将演示如何在支持 ROCm 的 AMD GPU 上使用 PyTorch 构建一个简单的深度学习推荐模型 (DLRM)。 简介 DLRM 位于推荐系统和深度学习的交汇…...

阿里云IIS虚拟主机部署ssl证书
宝塔配置SSL证书用起来是很方便的,只需要在站点里就可以配置好,但是云虚拟主机在管理的时候是没有这个权限的,只提供了简单的域名管理等信息。 此处记录下阿里云(原万网)的IIS虚拟主机如何配置部署SSL证书。 进入虚拟…...

Python运算符列表
运算符 描述 xy,x—y 加、减,“"号可重载为连接符 x*y,x**y,x/y,x%y 相乘、求平方、相除、求余,“*”号可重载为重复,“%"号可重载为格式化 <,<,&…...

MFC图形函数学习09——画多边形函数
这里所说的多边形是指在同一平面中由多条边构成的封闭图形,强调封闭二字,否则无法进行颜色填充,多边形包括凸多边形和凹多边形。 一、绘制多边形函数 原型:BOOL Polygon(LPPOINT lpPoints,int nCount); 参数&#x…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
