《数据结构》学习系列——图(中)
系列文章目录
目录
- 图的遍历
- 深度优先遍历
- 递归算法
- 堆栈算法
- 广度优先搜索
- 拓扑排序
- 定义定理
- 算法思想
- 伪代码
- 关键路径
- 基本概念
- 关键活动有关量
- 数学公式
- 伪代码
- 时间复杂性
图的遍历
- 从给定连通图的某一顶点出发,沿着一些边访问遍图中所有的顶点,且使每个顶点仅被访问一次,称为图的遍历(Graph Traversal)
- 存在的问题:图中可能存在回路,且图的任一顶点都可能与其它顶点相通,在访问完某个顶点之后可能会沿着某些边又回到曾经访问过的顶点。
- 避免重复访问:设置一个标志顶点是否被访问过的辅助数组 visited[],它的初始状态为 0。在图的遍历过程中,一旦某一个顶点 i i i 被访问,就立即让 visited[i] 置为 1,防止它被多次访问
深度优先遍历
- 深度优先遍历又被称为深度优先搜索 DFS (Depth First Search),其类似于树的先根遍历
- 基本思想:
- DFS在访问图中某一起始顶点 v v v 后,由 v v v 出发,访问它的任一邻接顶点 w 1 w_1 w1;再从 w 1 w_1 w1 出发,访问与 w 1 w_1 w1 邻接但还没有访问过的顶点 w 2 w_2 w2;然后再从 w 2 w_2 w2 出发,进行类似的访问。如此往下去,直至到达所有的邻接顶点都被访问过的顶点 u u u 为止。接着,退回一步,退到前一次访问过的顶点,看看还有其它没有被访问的邻接顶点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止

- DFS在访问图中某一起始顶点 v v v 后,由 v v v 出发,访问它的任一邻接顶点 w 1 w_1 w1;再从 w 1 w_1 w1 出发,访问与 w 1 w_1 w1 邻接但还没有访问过的顶点 w 2 w_2 w2;然后再从 w 2 w_2 w2 出发,进行类似的访问。如此往下去,直至到达所有的邻接顶点都被访问过的顶点 u u u 为止。接着,退回一步,退到前一次访问过的顶点,看看还有其它没有被访问的邻接顶点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;如果没有,就再退回一步进行搜索。重复上述过程,直到连通图中所有顶点都被访问过为止
递归算法
伪代码
// 图的深度优先遍历的递归算法
DepthFirstSearch(v, visited)
{visited[v] = 1;p = adjacent(Head[v]);while (p != NULL){if (visited[VerAdj(p) != 1]){DepthFirstSearch(VerAdj(p), visited)p = link(p); }}
}// 算法主体
DFS_Main()
{// 为辅助数组申请空间visited = new int[graphsize];// 数组初始化for (int k = 0; k < graphsize; k++){visited[k] = 0;// 从序号为0的顶点出发,深度优先遍历图DepthFirstSearch(0, visited)delete[] visited;}
}
非连通图需要多次调用深度优先遍历算法
for i = 0 to n-1
{for j = 0 to n-1{if visited[j] = 0{DepthFirstSearch(v[j], visited)}}
}
算法分析
- 图中有 n n n 个顶点, e e e 条边
- 如果用邻接表存储,沿顶点的adjacent可以找到某个顶点 v v v 的所有邻接顶点 w w w。由于总共有 2 e 2e 2e(无向图)或 e e e(有向图)个边结点,所以扫描边的时间为 O ( e ) O(e) O(e)。而且对所有顶点递归访问 1 次,所以遍历图的时间复杂性为 O ( n + e ) O(n + e) O(n+e)
- 如果用邻接矩阵存储,则查找每一个顶点的所有的边,所需时间为 O ( n ) O(n) O(n),则遍历图中所有的顶点所需的时间为 O ( n 2 ) O(n^2) O(n2)
堆栈算法
- 可以利用堆栈实现深度优先遍历的非递归算法
- 堆栈中存放已访问结点的还没有被访问的邻接顶点。每次弹出栈顶元素时,如其未被访问则访问该顶点,检查当前顶点的边链表,将还没有被访问的邻接顶点入栈,循环进行
基本思想
首先将所有顶点的visited[]值置为 0,初始顶点压入堆栈
- ① 检测堆栈是否为空。若堆栈为空,则迭代结束;否则,从栈顶弹出一个顶点 v v v
- ② 如果 v v v 未被访问过,则访问 v v v,将visited[v]值更新为 1,然后根据 v v v 的邻接顶点表,将 v v v 的未被访问的邻接顶点压入栈,执行步骤 ①
// 非递归实现深度优先遍历算法
void DFS(Graph &graph, int v) {stack<int> S; // 创建栈Svector<bool> visited(graph.size(), false); // 初始化访问标记数组S.push(v); // 将起始顶点压入栈while (!S.empty()) { // 当栈不为空时int v = S.top(); // 弹出栈顶元素S.pop();if (!visited[v]) {cout << v << " "; // 访问顶点visited[v] = true; // 标记为已访问// 获取顶点v的所有邻接顶点,并压入栈中for (auto p = graph.adjacent(v); p != nullptr; p = p->link) {if (!visited[p->VerAdj]) {S.push(p->VerAdj);}}}}
}
算法分析
- 如果使用邻接表表示图,则循环的总时间代价为 d 0 + d 1 + ⋯ + d n − 1 = O ( e ) d_0 + d_1 + \dots + d_{n-1} = O(e) d0+d1+⋯+dn−1=O(e),其中 d i d_i di 是顶点 i i i 的度(无向图)或出度(有向图)。总的时间复杂度为 O ( n + e ) O(n + e) O(n+e)
- 如果使用邻接矩阵,则对于每一个被访问的顶点,循环要检测矩阵中的 n n n 个元素,总的时间代价为 O ( n 2 ) O(n^2) O(n2)
广度优先搜索
- 为了实现逐层访问,算法中使用了一个队列,以记忆正在访问的这一层和上一层的顶点,以便于向下一层访问
- 与深度优先搜索过程一样,为避免重复访问,需要一个辅助数组visited[],为被访问过的顶点加标记
// BFS1 [初始化]
CREATEQ(Q); // 创建队列 Q
for (int i = 1; i <= n; i++) visited[i] = 0; // 初始化所有顶点为未访问
PRINT(v); // 打印起始顶点
visited[v] = 1; // 标记起始顶点为已访问
Q.enqueue(v); // 起始顶点入队列// BFS2 [广度优先遍历]
while (!Q.isEmpty()) { // 当队列不为空时v = Q.dequeue(); // 队头元素出队p = adjacent(Head[v]); // 获取当前顶点的邻接链表while (p != NULL) { // 遍历邻接链表if (visited[p->VerAdj] == 0) { // 如果邻接顶点未被访问Q.enqueue(p->VerAdj); // 将邻接顶点入队PRINT(p->VerAdj); // 打印邻接顶点visited[p->VerAdj] = 1; // 标记邻接顶点为已访问}p = p->link; // 继续访问下一个邻接顶点}
}算法分析
- 如果使用邻接表表示图,则循环的总时间代价为 d 0 + d 1 + ⋯ + d n − 1 = O ( e ) d_0 + d_1 + \dots + d_{n-1} = O(e) d0+d1+⋯+dn−1=O(e),其中 d i d_i di 是顶点 i i i 的度。总的时间复杂度为 O ( n + e ) O(n + e) O(n+e)
- 如果使用邻接矩阵,则对于每一个被访问的顶点,循环要检测矩阵中的 n n n 个元素,总的时间代价为 O ( n 2 ) O(n^2) O(n2)
拓扑排序
- AOV 网:在有向图中,用顶点表示活动,用有向边表示活动之间的先后关系,称这样的有向图为AOV网 (Activity On Vertex Network)}
- 计划、施工过程、生产流程、程序流程等都是“工程”。除了很小的工程外,一般都把工程分为若干个叫做“活动”的子工程。完成了所有这些活动,这个工程就可以完成了
- 例如,计算机专业学生的学习就是一个工程,每一门课程的学习就是整个工程的一些活动。其中有些课程要求先修课程,有些则不要求。这样,在有些课程之间有先后关系,有些课程可以并行地学习

定义定理
- 在 AOV 网络中,如果活动 V i V_i Vi 必须在活动 V j V_j Vj 之前进行,则存在有向边 ⟨ V i , V j ⟩ \langle V_i, V_j \rangle ⟨Vi,Vj⟩
- AOV 网络中不能出现有向回路,即有向环。在 AOV 网络中如果出现了有向环,则意味着某项活动应以自己作为先决条件。因此,对给定的 AOV 网络,必须先判断它是否存在有向环
- 拓扑序列:AOV 网中所有顶点排成的线性序列,要求每个活动的所有前驱活动都排在该活动前面
- 拓扑排序:构造 AOV 网的拓扑序列的过程被称为拓扑排序
- 如果通过拓扑排序能将 AOV 网络的所有顶点都排入一个拓扑有序的序列中,则该 AOV 网络中必定不会出现有向环;相反,如果得不到满足要求的拓扑有序序列,则说明 AOV 网络中存在有向环,此 AOV 网络所代表的工程是不可行的
- 设图 G = ( V , E ) G = (V, E) G=(V,E) 是非循环图, V ( G ) ≠ ∅ V(G) \neq \emptyset V(G)=∅,则 G G G 中一定存在入度为零的顶点。
- 设 G = ( V , E ) G = (V, E) G=(V,E) 是非循环图, V ( G ) = { 1 , 2 , … , n } V(G) = \{1, 2, \dots, n\} V(G)={1,2,…,n}, e = ∣ E ( G ) ∣ e = |E(G)| e=∣E(G)∣。则算法是正确的,且算法的时间复杂性为 O ( n + e ) O(n + e) O(n+e)
算法思想
- 拓扑排序算法的基本步骤
- 从网中选择一个入度为 0 的顶点并将其输出
- 从网中删除该顶点及其所有出边
- 执行步骤 ① 和 ②,直至所有顶点都已输出,或网中剩余顶点入度均不为 0(说明网中存在回路,无法继续拓扑排序)
注意:对于任何无回路的 AOV 网,其顶点均可排成拓扑序列,但其拓扑序列未必唯一

伪代码
- 假定 AOV 网用邻接表的形式存储。为实现拓扑排序算法,事先需做好两项准备工作:
- 建立一个数组count[],count[i]的元素值为顶点 i i i 的入度;
- 建立一个堆栈,栈中存放入度为 0 的顶点,每当一个顶点的入度为 0,就将其压入栈
// TOrder1 [初始化]
// 计算 count 数组(每个顶点的入度)
for (int i = 1; i <= n; i++) count[i] = 0; // 初始化所有顶点的入度为 0// 遍历邻接表,计算每个顶点的入度
for (int i = 1; i <= n; i++) {p = adjacent(Head[i]); // 获取顶点 i 的邻接表头指针while (p != NULL) { // 遍历邻接表count[VerAdj(p)]++; // 更新邻接顶点的入度p = p->link; // 移动到下一个邻接点}
}// 拓扑排序
top = 0; // 栈顶指针初始化为 0// 将入度为 0 的顶点压入栈
for (int i = 1; i <= n; i++) {if (count[i] == 0) {stack[top] = i; // 顶点 i 入栈top++; // 栈顶指针加 1}
}for (int i = 1; i <= n; i++) {// 如果循环体执行了 n 次但栈为空,则说明图中存在回路if (top == 0) {PRINT("There is a cycle in the network!");RETURN;} else {// 栈顶元素出栈j = stack[top - 1];top--; // 栈顶指针减 1PRINT(j); // 输出顶点 j(拓扑序中的一个顶点)// 遍历顶点 j 的邻接表,更新邻接顶点的入度p = adjacent(Head[j]);while (p != NULL) {k = VerAdj(p); // 获取邻接顶点count[k]--; // 邻接顶点的入度减 1if (count[k] == 0) { // 如果邻接顶点入度变为 0,则压入栈stack[top] = k;top++;}p = p->link; // 继续遍历下一个邻接点}}
}关键路径
基本概念
-
如果在有向无环的带权图中
- 用有向边表示一个工程中的各项活动 (Activity)
- 用边上的权值表示活动的持续时间 (Duration)
- 用顶点表示事件 (Event)
-
则这样的有向图叫做用边表示活动的网络,简称AOE (Activity On Edges) 网络
- 源点:表示整个工程的开始(入度为零)
- 汇点:表示整个工程的结束(出度为零)
-
在 AOE 网络中,有些活动必须顺序进行,有些活动可以并行进行
-
从源点到各个顶点,以至从源点到汇点的有向路径可能不止一条。这些路径的长度也可能不同。完成不同路径的活动所需的时间虽然不同,但只有各条路径上所有活动都完成了,整个工程才算完成
-
完成整个工程所需的时间取决于从源点到汇点的最长路径长度,即在这条路径上所有活动的持续时间之和。这条路径长度最长的路径被称为关键路径 (Critical Path)
-
关键路径:从源点到汇点具有最大长度的路径称为关键路径
-
路径长度:指路径上的各边权值之和
-
关键活动:关键路径上的活动

关键活动有关量
-
事件 v j v_j vj 的最早发生时间ve(j):
- 从源点 v 0 v_0 v0 到 v j v_j vj 的最长路径长度。
-
事件 v j v_j vj 的最迟发生时间vl(j):
- 保证汇点的最早发生时间不推迟(即不推迟整个工程完成时间)的前提下,事件 v j v_j vj 允许的最迟发生时间,等于ve(n-1)减去从 v j v_j vj 到 v n − 1 v_{n-1} vn−1 的最长路径长度
-
活动 a i a_i ai 的最早开始时间e(i):
- 设活动 a i a_i ai 在有向边 ⟨ v j , v k ⟩ \langle v_j, v_k \rangle ⟨vj,vk⟩ 上,e(i)是从源点 v 0 v_0 v0 到 v j v_j vj 的最长路径长度。因此e(i) = ve(j)
-
活动 a i a_i ai 的最迟开始时间l(i):
- l(i)是在不会引起时间延误的前提下,该活动允许的最迟开始时间。设活动 a i a_i ai 在有向边 ⟨ v j , v k ⟩ \langle v_j, v_k \rangle ⟨vj,vk⟩ 上,则 l ( i ) = vl(k) − weight ( ⟨ j , k ⟩ ) l(i) = \texttt{vl(k)} - \texttt{weight}(\langle j, k \rangle) l(i)=vl(k)−weight(⟨j,k⟩)
数学公式
-
求所有事件的最早发生时间}:
递推公式: // 拓扑排序正序
ve(k) = { 0 , k = 0 max { ve(j) + weight ( ⟨ j , k ⟩ ) } , ⟨ v j , v k ⟩ ∈ E ( G ) , k = 1 , 2 , … , n − 1 \texttt{ve(k)} = \begin{cases} 0, & k = 0 \\ \max\{\texttt{ve(j)} + \texttt{weight}(\langle j, k \rangle)\}, & \langle v_j, v_k \rangle \in E(G), \; k = 1, 2, \dots, n-1 \end{cases} ve(k)={0,max{ve(j)+weight(⟨j,k⟩)},k=0⟨vj,vk⟩∈E(G),k=1,2,…,n−1 -
求所有事件的最迟发生时间}:
递推公式:拓扑排序逆序
vl(j) = { ve(n-1) , j = n − 1 min { vl(k) − weight ( ⟨ j , k ⟩ ) } , ⟨ v j , v k ⟩ ∈ E ( G ) , j = n − 2 , n − 3 , … , 0 \texttt{vl(j)} = \begin{cases} \texttt{ve(n-1)}, & j = n-1 \\ \min\{\texttt{vl(k)} - \texttt{weight}(\langle j, k \rangle)\}, & \langle v_j, v_k \rangle \in E(G), \; j = n-2, n-3, \dots, 0 \end{cases} vl(j)={ve(n-1),min{vl(k)−weight(⟨j,k⟩)},j=n−1⟨vj,vk⟩∈E(G),j=n−2,n−3,…,0
伪代码
思路
求关键活动的基本步骤:
- 对 AOE 网进行拓扑排序,若网中有回路,则终止算法;按拓扑次序求出各顶点事件的最早发生时间 ve
- 按拓扑序列的逆序求出各顶点事件的最迟发生时间 vl
- 根据ve和vl的值,求出各活动的最早开始时间 e(i)与最迟开始时间l(i),若e(i) = l(i),则 i i i 是关键活动

// CPath1 - 计算事件的最早发生时间
// 初始化事件的最早发生时间
for (int i = 1; i <= n; i++) ve[i] = 0; // 最早发生时间初始化为 0// 按拓扑序计算事件的最早发生时间
for (int i = 1; i <= n; i++) {p = adjacent(Head[i]); // 获取顶点 i 的邻接表while (p != NULL) {k = VerAdj(p); // 获取邻接顶点if (ve[i] + cost(p) > ve[k]) // 更新最早发生时间ve[k] = ve[i] + cost(p);p = p->link; // 继续访问下一个邻接点}
}// CPath2 - 计算事件的最迟发生时间
// 初始化事件的最迟发生时间
for (int i = 1; i <= n; i++) vl[i] = ve[n]; // 最迟发生时间初始化为最后事件的最早时间// 按拓扑逆序计算事件的最迟发生时间
for (int i = n; i >= 1; i--) {p = adjacent(Head[i]); // 获取顶点 i 的邻接表while (p != NULL) {k = VerAdj(p); // 获取邻接顶点if (vl[k] - cost(p) < vl[i]) // 更新最迟发生时间vl[i] = vl[k] - cost(p);p = p->link; // 继续访问下一个邻接点}
}// CPath3 - 关键活动的最早开始时间和最迟开始时间
// 遍历所有活动,计算关键活动
for (int i = 1; i <= n; i++) {p = adjacent(Head[i]); // 获取顶点 i 的邻接表while (p != NULL) {k = VerAdj(p); // 获取邻接顶点e = ve[i]; // 最早开始时间l = vl[k] - cost(p); // 最迟开始时间if (e == l) // 如果最早时间等于最迟时间,则为关键活动PRINT("<", i, ",", k, "> is Critical Activity!");p = p->link; // 继续访问下一个邻接点}
}时间复杂性
- 时间复杂性:对顶点进行拓扑排序的时间复杂性为 O ( n + e ) O(n + e) O(n+e),以拓扑次序求ve[i]和按拓扑逆序求vl[i]}时,所需时间均为 O ( e ) O(e) O(e)。求各个活动的e[k]和l[k]的时间复杂度为 O ( e ) O(e) O(e),整个算法的时间复杂性是 O ( n + e ) O(n + e) O(n+e)
- 定理 6.3:任意的非空 AOE 网至少存在一条关键路径
- 推论 6.1:假设边 ⟨ T i , T j ⟩ \langle T_i, T_j \rangle ⟨Ti,Tj⟩ 属于 AOE 网,则有
vl[j] − ve[i] ≥ Weight ( ⟨ T i , T j ⟩ ) \texttt{vl[j]} - \texttt{ve[i]} \geq \texttt{Weight}(\langle T_i, T_j \rangle) vl[j]−ve[i]≥Weight(⟨Ti,Tj⟩) - 且如果 ⟨ T i , T j ⟩ \langle T_i, T_j \rangle ⟨Ti,Tj⟩ 属于某一条关键路径,则有
vl[j] − ve[i] = Weight ( ⟨ T i , T j ⟩ ) . \texttt{vl[j]} - \texttt{ve[i]} = \texttt{Weight}(\langle T_i, T_j \rangle). vl[j]−ve[i]=Weight(⟨Ti,Tj⟩).
相关文章:

《数据结构》学习系列——图(中)
系列文章目录 目录 图的遍历深度优先遍历递归算法堆栈算法 广度优先搜索 拓扑排序定义定理算法思想伪代码 关键路径基本概念关键活动有关量数学公式伪代码时间复杂性 图的遍历 从给定连通图的某一顶点出发,沿着一些边访问遍图中所有的顶点,且使每个顶点…...

探索Python的HTTP之旅:揭秘Requests库的神秘面纱
文章目录 **探索Python的HTTP之旅:揭秘Requests库的神秘面纱**第一部分:背景介绍第二部分:Requests库是什么?第三部分:如何安装Requests库?第四部分:Requests库的五个简单函数使用方法第五部分&…...

Python 爬虫从入门到(不)入狱学习笔记
爬虫的流程:从入门到入狱 1 获取网页内容1.1 发送 HTTP 请求1.2 Python 的 Requests 库1.2 实战:豆瓣电影 scrape_douban.py 2 解析网页内容2.1 HTML 网页结构2.2 Python 的 Beautiful Soup 库 3 存储或分析数据(略) 一般爬虫的基…...
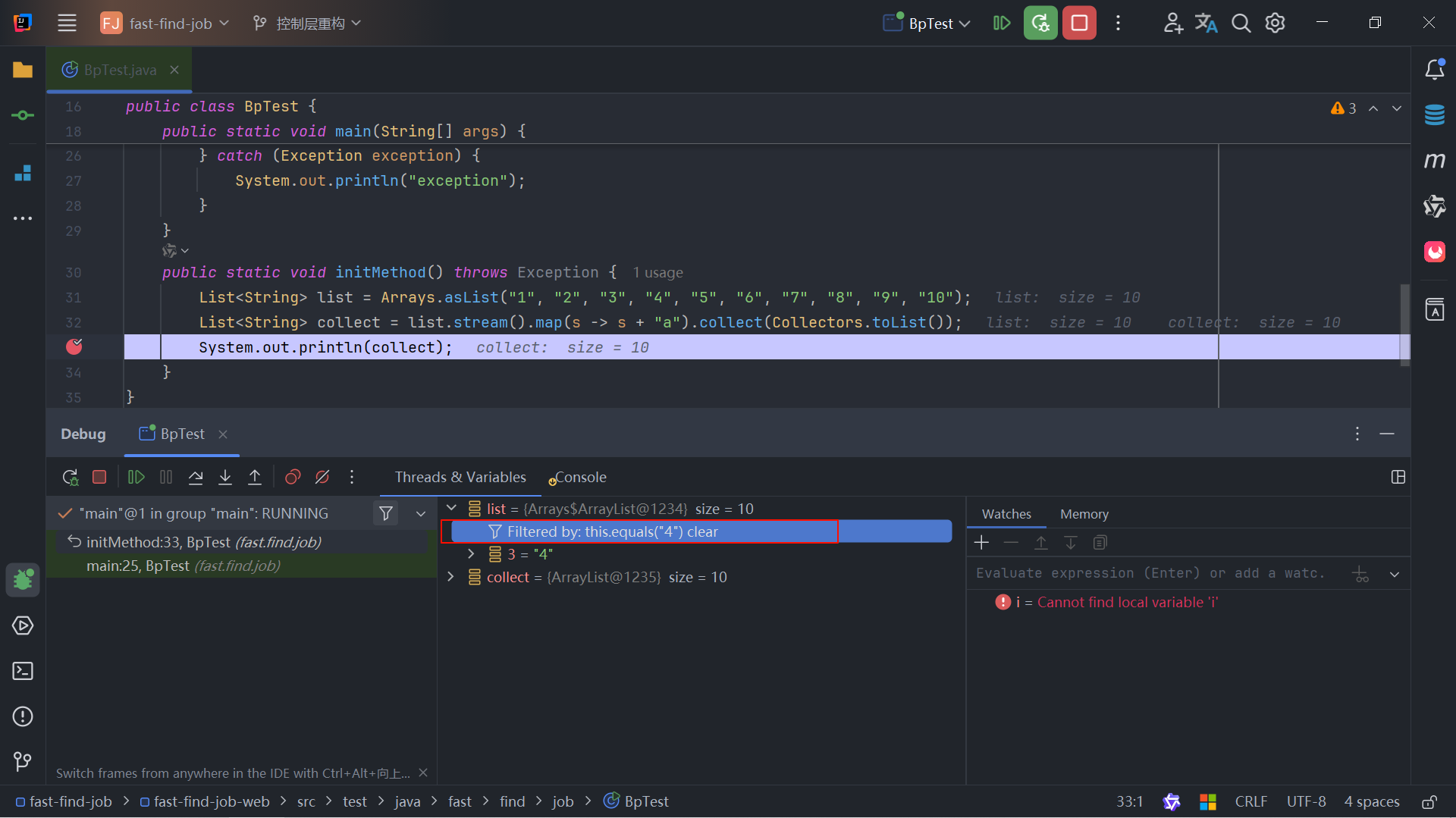
IDEA优雅debug
目录 引言一、断点分类🎄1.1 行断点1.2 方法断点1.3 属性断点1.4 异常断点1.5 条件断点1.6 源断点1.7 多线程断点1.8 Stream断点 二、调试动作✨三、Debug高级技巧🎉3.1 watch3.2 设置变量3.3 异常抛出3.4 监控JVM堆大小3.5 数组过滤和筛选 引言 使用ID…...

wp the_posts_pagination 与分类页面搭配使用
<ul> <?php while( have_posts() ) : the_post(); <li > <a href"<?php the_permalink(); ?>"> <?php xizhitbu_get_thumbnail(thumb-pro); ?> </a> <p > <a href&q…...

大数据-231 离线数仓 - DWS 层、ADS 层的创建 Hive 执行脚本
点一下关注吧!!!非常感谢!!持续更新!!! Java篇开始了! 目前开始更新 MyBatis,一起深入浅出! 目前已经更新到了: Hadoop࿰…...

【Python】分割秘籍!掌握split()方法,让你的字符串处理轻松无敌!
在Python开发中,字符串处理是最常见也是最基础的任务之一。而在众多字符串操作方法中,split()函数无疑是最为重要和常用的一个。无论你是Python新手,还是经验丰富的开发者,深入理解并熟练运用split()方法,都将大大提升…...

免费实用在线AI工具集合 - 加菲工具
免费在线工具-加菲工具 https://orcc.online/ 在线录屏 https://orcc.online/recorder 时间戳转换 https://orcc.online/timestamp Base64 编码解码 https://orcc.online/base64 URL 编码解码 https://orcc.online/url Hash(MD5/SHA1/SHA256…) 计算 https://orcc.online/h…...

正则表达式灾难:重新认识“KISS原则”的意义
RSS Feed 文章标题整理 微积分在生活中的应用与思维启发 捕鹿到瞬时速度的趣味探索 微积分是一扇通往更广阔世界的门,从生活中学习思维的工具。 数据库才是最强架构 你还在被“复杂架构”误导吗? 把业务逻辑写入数据库,重新定义简单与效率。…...

eNSP-缺省路由配置
缺省路由是一种特殊的静态路由,其目的地址为0.0.0.0,子网掩码为0.0.0.0。 1.拓扑图搭建 2.配置路由器 AR2 <Huawei>sys #进入系统视图 [Huawei]ip route-static 0.0.0.0 0.0.0.0 192.168.3.2 #设置缺省路由 [Huawei]q #返回上一层 <Huawe…...

solr 远程命令执行 (CVE-2019-17558)
漏洞描述 Apache Velocity是一个基于Java的模板引擎,它提供了一个模板语言去引用由Java代码定义的对象。Velocity是Apache基金会旗下的一个开源软件项目,旨在确保Web应用程序在表示层和业务逻辑层之间的隔离(即MVC设计模式)。 Apa…...

STM32端口模拟编码器输入
文章目录 前言一、正交编码器是什么?二、使用步骤2.1开启时钟2.2配置编码器引脚 TIM3 CH1(PA6) CH2 (PA7)上拉输入2.3.初始化编码器时基2.4 初始化编码器输入2.5 配置编码器接口2.6 开启定时器2.7获取编码器数据 三、参考程序四、测试结果4.1测试方法4.2串口输出结果…...

Centos 8, add repo
Centos repo前言 Centos 8更换在线阿里云创建一键更换repo 自动化脚本 华为Centos 源 , 阿里云Centos 源 华为epel 源 , 阿里云epel 源vim /centos8_repo.sh #!/bin/bash # -*- coding: utf-8 -*- # Author: make.han...
)
MYSQL- 查看存储过程调式信息语句(二十七)
13.7.5.27 SHOW PROCEDURE CODE 语句 SHOW PROCEDURE CODE proc_name此语句是MySQL扩展,仅适用于已构建有调试支持的服务器。它显示了命名存储过程的内部实现的表示。类似的语句SHOW FUNCTION CODE显示有关存储函数的信息(见第13.7.5.19节“SHOW FUNTIO…...

C#基础上机练习题
21.计算500-800区间内素数的个数cn,并按所求素数的值从大到小的顺序排列,再计算其间隔加、减之和,即第1个素数-第2个素数第3个素数-第4个素数第5个素数……的值sum。请编写函数实现程序的要求,把结果cn和sum输出。 22.在三位整数…...

5.5 W5500 TCP服务端与客户端
文章目录 1、TCP介绍2、W5500简介2.1 关键函数socketlistensendgetSn_RX_RSRrecv自动心跳包检测getSn_SR 1、TCP介绍 TCP 服务端: 创建套接字[socket]:服务器首先创建一个套接字,这是网络通信的端点。绑定套接字[bind]:服务器将…...
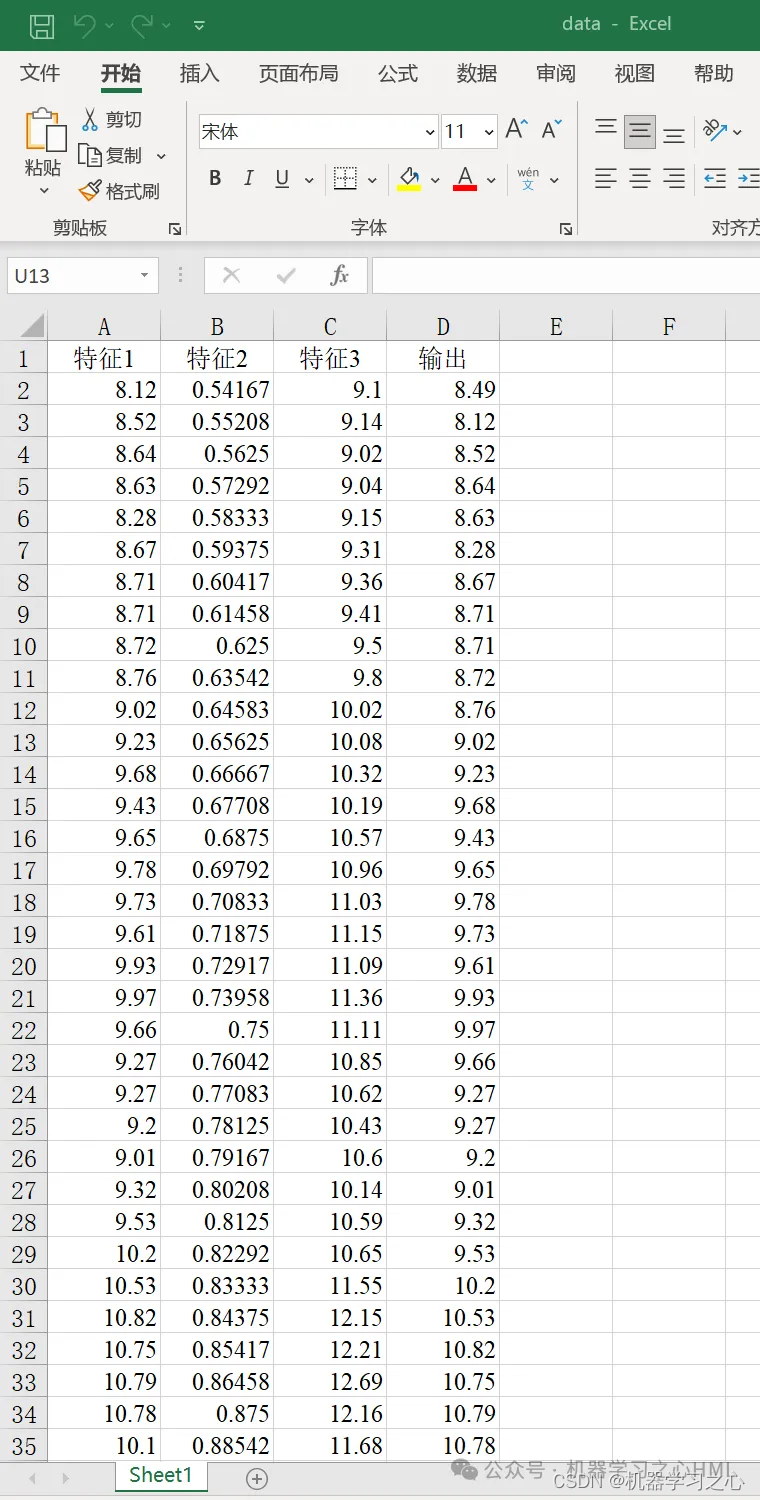
一区北方苍鹰算法优化+创新改进Transformer!NGO-Transformer-LSTM多变量回归预测
一区北方苍鹰算法优化创新改进Transformer!NGO-Transformer-LSTM多变量回归预测 目录 一区北方苍鹰算法优化创新改进Transformer!NGO-Transformer-LSTM多变量回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab NGO-Transformer-LST…...

深入理解 MyBatis 的缓存机制:一级缓存与二级缓存
MyBatis 是目前 Java 开发中常用的一种 ORM(对象关系映射)框架,它不仅简化了 SQL 语句的编写和管理,还提供了强大的缓存机制,用以提高数据库访问的性能。MyBatis 的缓存分为一级缓存和二级缓存,分别应用于不…...

移远通信推出全新5G RedCap模组RG255AA系列,以更高性价比加速5G轻量化大规模商用
11月20,全球领先的物联网整体解决方案供应商移远通信宣布,正式推出其全新5G RedCap模组RG255AA系列。该系列模组支持5G NR独立组网(SA)和LTE Cat 4双模通信,具有高性能高集成度、低功耗、小尺寸、高性价比等优势&#…...

架构-微服务-环境搭建
文章目录 前言一、案例准备1. 技术选型2. 模块设计3. 微服务调用 二、创建父工程三、创建基础模块四、创建用户微服务五、创建商品微服务六、创建订单微服务 前言 微服务环境搭建 使用的电商项目中的商品、订单、用户为案例进行讲解。 一、案例准备 1. 技术选型 maven&a…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
