动态规划之背包问题
0/1背包问题
1.二维数组解法
题目描述:有一个容量为m的背包,还有n个物品,他们的重量分别为w1、w2、w3.....wn,他们的价值分别为v1、v2、v3......vn。每个物品只能使用一次,求可以放进背包物品的最大价值。
输入样例:
10 4
2 1
3 3
4 5
7 9
输出样例:
12
解:
符号描述:i表示第i个物品,背包容量为j,dp[i][j]表示从下标为0到i,背包容量为j时任意选取物品所得价值的最大值。所以全局的最优解就是dp[m][n]
背包问题和函数的递归很像,只不过函数递归时从结果去接近边界,而背包问题是从边界出发,从小问题逐步去接近最终所要求的最优解。
先创建一个二维数组

可以看到当背包容量为零,或者可选物品为0时,他的局部最优解都是0

然后从每一行的左到右开始遍历(具体是为什么可以自己试一试)
- 当背包容量为1时由于第一个物品的重量为2无法放进去,所以dp[1][1]=0;
- 当背包容量为2时可以放进第一个物品,dp[2][1]=1;
- 当背包容量大于2时,后续的最大价值都是1;

接着看第二行,这个第二行的含义就是当背包物品容量从1到j变化时,任意选物品1-2的最优解
先放的i=2的物品,然后看剩余重量能容纳的上一行的局部最优解。最后还要判断是否这个最优解比上一行同一列的最优解更大,如果更大就更新状态,否则就继承状态。
- j=1;dp[2][1]=0; 继承上一行的状态
- j=2;dp[2][2]=0; 0<1,继承上一行的状态
- j=3;dp[2][3]=3+dp[2][0]=3 ,3>1,更新状态使dp[2][3]=3;
- j=4;dp[2][4]=3+dp[2][1]=3,同样状态更新
- j=5;dp[2][5]=3+dp[1][2]=4,4>1 状态更新。
后面也是同理。

再看第三行
j从零到三无法当下第三个物品,所以此时的最优解依然是前两个物品最优选择的最优解,依旧继承上一行的状态。
然后从第4列开始,物品3就可以被放下
- j=4,dp[3][4]=5+dp[2][0]=5,5>3,状态更新
- j=5,dp[3][5]=5+dp[2][1]=5,5>4,状态更新
- j=6,dp[3][6]=5+dp[2][2]=6,6>4,状态更新

我想你聪明如你已经看到规律了,接着写出第4行

所以得出来全局的最优解就是12
下面来看代码:
#include<iostream>
#include<algorithm>using namespace std;//学校的IDE有点老,好像不支持algorithm里的max
int max(int x,int y)
{return x>y?x:y;
}int m,n;
int dp[30][30]={0};//初始化全部设置为0
int w[30];//重量
int v[30];//价值
//0/1背包问题
int main()
{cin>>m>>n;int i=0,j=0;//输入w,vfor(i=1;i<=n;i++){cin>>w[i]>>v[i];}//主要的循环体for(i=1;i<=n;i++)//物品编号遍历{for(j=1;j<=m;j++)//背包重量遍历{if(j<w[i])//这个物品无法放进去,继承上一行的状态{dp[i][j]=dp[i-1][j];}else//判断当前最优解与上一行的最优解谁更大{dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);}}}cout<<dp[n][m]<<endl;return 0;
}
2.一维数组滚动解法
我们注意到二维数组的解法的时间复杂度是m*n,空间复杂度是m*n
而暴力求解的时间复杂度是2^n,空间复杂度也是m*n
二维数组法确实优化的时间复杂度,但是空间复杂度却和暴力一样,因此便有了一维数组滚动解法来进一步优化。
我们在上面的分析中,一步步的更新局部最优解,最终得到所求的最优解。但是有时候并没有更新元素而是继承上一行的最优解,那么是不是就可以只用一个一维数组来存储第i行的最优解,然后需要更新的时候更新一下就可以了。

这时候我们就可以把原有的代码稍作修改:
#include<iostream>
#include<algorithm>using namespace std;//学校的IDE有点老,好像不支持algorithm里的max
int max(int x,int y)
{return x>y?x:y;
}int m,n;
int dp[30]={0};//初始化全部设置为0
int w[30];//重量
int v[30];//价值
//0/1背包问题
int main()
{cin>>m>>n;int i=0,j=0;//输入w,vfor(i=1;i<=n;i++){cin>>w[i]>>v[i];}//主要的循环体for(i=1;i<=n;i++){for(j=m;j>=w[i];j--)//从最右边遍历,后面的多重背包是从做左到右遍历注意区分。{dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}cout<<dp[m]<<endl;return 0;
}
电脑验证
二维数组:

完全背包问题
题目描述:有一个容量为m的背包,还有n个物品,他们的重量分别为w1、w2、w3.....wn,他们的价值分别为v1、v2、v3......vn。每个物品有无限个,求可以放进背包物品的最大价值。
输入样例:10 4 2 1 3 3 4 6 8 10
输出样例:13

完全背包区别于0/1背包就是每个物品的选择没有次数限制。
它们的解题思路的区别在于主要的循环体那,完全背包需要先继承上一层的状态,然后考虑能不能放下,如果不能那这个位置的最优解就是上层位置的最优解,否则就把这个物品放进来,再加上背包容量为j-w[i]的同层位置的最优解(同层是因为物品个数没有限制),这样就可以完成叠加。
二维数组法
来看代码:
#include<iostream>
#include<algorithm>using namespace std;int m,n;
int dp[30][30]={0};
int w[30];
int v[30];
//完全背包问题
int main()
{int i,j;//输入m,ncin>>m>>n;// 输入w,vfor(i=1;i<=n;i++){cin>>w[i]>>v[i];} //主要循环体 for(i=1;i<=n;i++){for(j=1;j<=m;j++){//完全背包要先继承上一层状态dp[i][j]=dp[i-1][j];if(j>=w[i]){dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);} }}cout<<dp[n][m]<<endl;return 0;
}

一维数组滚动解法
这个解法同样也是为了降低空间复杂度

所以以同样的方法优化一下代码:
#include<iostream>
#include<algorithm>using namespace std;int m,n;
int dp[30]={0};
int w[30];
int v[30];
//完全背包问题
int main()
{int i,j;//输入m,ncin>>m>>n;// 输入w,vfor(i=1;i<=n;i++){cin>>w[i]>>v[i];} //主要循环体 for(i=1;i<=n;i++){for(j=w[i];j<=m;j++){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}cout<<dp[m]<<endl;return 0;
}

电脑验证
二维数组法:

一维数组滚动法:

多重背包问题
多重背包问题与前面两个问题的区别也是在物品的数量上,这次它换成了有限个。
题目描述:有一个容量为m的背包,还有n个物品,他们的重量分别为w1、w2、w3.....wn,他们的价值分别为v1、v2、v3......vn,它们的数量分别有c1、c2、c3......cn个,求可以放进背包物品的最大价值。
输入样例:
10 3
2 1 6
6 10 3
3 6 3
输出样例:
转换成传统的0/1背包问题
这个方法比较容易想到,就不过多赘述了

看代码:
#include<iostream>
#include<algorithm>using namespace std;int m,n;
int dp[30]={0};
int w[30];
int v[30];
int c[30];
int main()
{int i,j,k;//输入m,ncin>>m>>n;//输入w,v,c(数量) for(i=1;i<=n;i++){cin>>w[i]>>v[i]>>c[i];} for(i=1;i<=n;i++){for(k=1;k<=c[i];k++)//多次模拟0/1背包 {for(j=m;j>=w[i];j--)//一维滚动法 {dp[j]=max(dp[j],dp[j-w[i]]+v[i]); }}}for(i=1;i<=m;i++)//这里直接电脑验证了 {cout<<dp[i]<<" ";}cout<<endl;cout<<dp[m];return 0;} //10 3 2 1 6 6 10 3 3 6 3

特别感谢某站T_zhao 老师的讲解,讲的很明白。
相关文章:

动态规划之背包问题
0/1背包问题 1.二维数组解法 题目描述:有一个容量为m的背包,还有n个物品,他们的重量分别为w1、w2、w3.....wn,他们的价值分别为v1、v2、v3......vn。每个物品只能使用一次,求可以放进背包物品的最大价值。 输入样例…...

【Python】 深入理解Python的单元测试:用unittest和pytest进行测试驱动开发
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 单元测试是现代软件开发中的重要组成部分,通过验证代码的功能性、准确性和稳定性,提升代码质量和开发效率。本文章深入介绍Python中两种主流单元测试框架:unittest和pytest,并结合测试驱动开发(TDD)…...

Java集合1.0
1.什么是集合? 集合就是一个存放数据的容器,准确的说是放数据对象引用的容器。 集合和数组的区别 数组是固定长度,集合是可变长度。数组可以存储基本数据类型,也可以存储引用数据类型,集合只能存储引用数据类型&…...

Leetcode 336 回文对
示例 1: 输入:words ["abcd","dcba","lls","s","sssll"] 输出:[[0,1],[1,0],[3,2],[2,4]] 解释:可拼接成的回文串为 ["dcbaabcd","abcddcba","sl…...

实现一个可配置的TCP设备模拟器,支持交互和解析配置
前言 诸位在做IOT开发的时候是否有遇到一个问题,那就是模拟一个设备来联调测试,虽然说现在的物联网通信主要是用mqtt通信,但还是有很多设备使用TCP这种协议交互,例如充电桩,还有一些工业设备,TCP这类报文交…...

算法的空间复杂度
空间复杂度 空间复杂度主要是衡量一个算法运行所需要的额外空间,在计算机发展早期,计算机的储存容量很小,所以空间复杂度是很重要的。但是经过计算机行业的迅速发展,计算机的容量已经不再是问题了,所以如今已经不再需…...
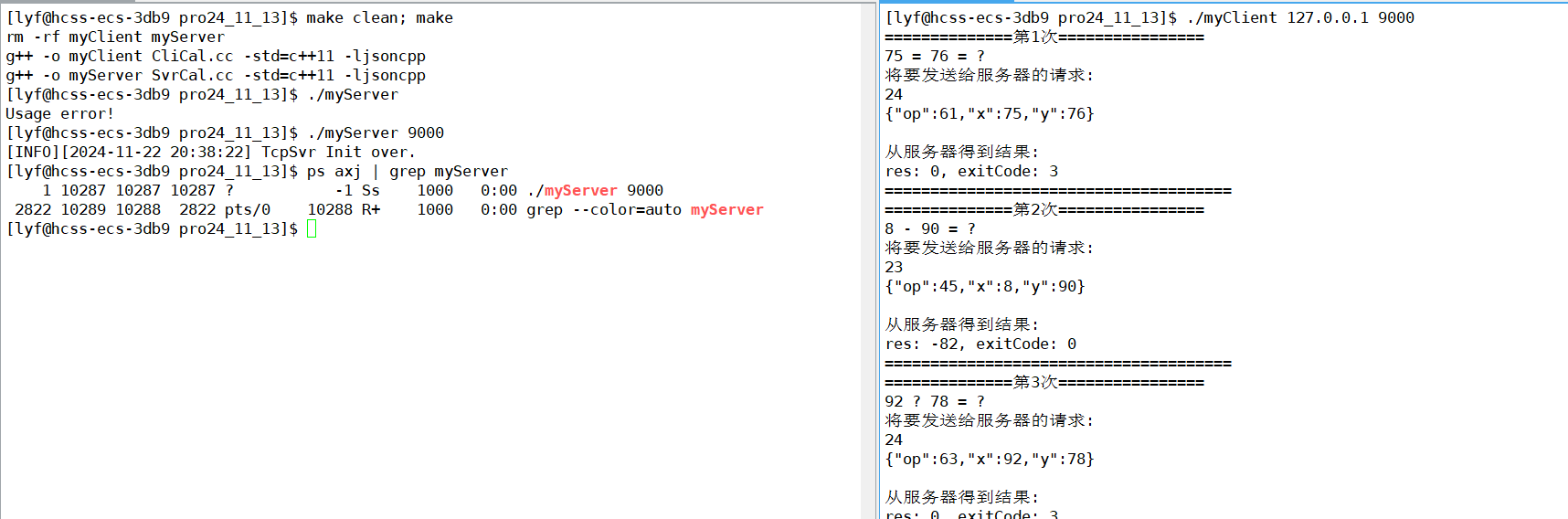
自定义协议
1. 问题引入 问题:TCP是面向字节流的(TCP不关心发送的数据是消息、文件还是其他任何类型的数据。它简单地将所有数据视为一个字节序列,即字节流。这意味着TCP不会对发送的数据进行任何特定的边界划分,它只是确保数据的顺序和完整…...

在 Taro 中实现系统主题适配:亮/暗模式
目录 背景实现方案方案一:CSS 变量 prefers-color-scheme 媒体查询什么是 prefers-color-scheme?代码示例 方案二:通过 JavaScript 监听系统主题切换 背景 用Taro开发的微信小程序,需求是页面的UI主题想要跟随手机系统的主题适配…...

autogen框架中使用chatglm4模型实现react
本文将介绍如何使用使用chatglm4实现react,利用环境变量、Tavily API和ReAct代理模式来回答用户提出的问题。 环境变量 首先,我们需要加载环境变量。这可以通过使用dotenv库来实现。 from dotenv import load_dotenv_ load_dotenv()注意.env文件处于…...

读《Effective Java》笔记 - 条目9
条目9:与try-finally 相比,首选 try -with -resource 什么是 try-finally? try-finally 是 Java 中传统的资源管理方式,通常用于确保资源(如文件流、数据库连接等)被正确关闭。 BufferedReader reader n…...
【软件入门】Git快速入门
Git快速入门 文章目录 Git快速入门0.前言1.安装和配置2.新建版本库2.1.本地创建2.2.云端下载 3.版本管理3.1.添加和提交文件3.2.回退版本3.2.1.soft模式3.2.2.mixed模式3.2.3.hard模式3.2.4.使用场景 3.3.查看版本差异3.4.忽略文件 4.云端配置4.1.Github4.1.1.SSH配置4.1.2.关联…...

nextjs window is not defined
问题产生的原因 在 Next.js 中,“window is not defined” 错误通常出现在服务器端渲染(Server - Side Rendering,SSR)的代码中。这是因为window对象是浏览器环境中的全局对象,在服务器端没有window这个概念。例如&am…...

C语言实现冒泡排序:从基础到优化全解析
一、什么是冒泡排序? 冒泡排序(Bubble Sort)是一种经典的排序算法,其工作原理非常直观:通过多次比较和交换相邻元素,将较大的元素“冒泡”到数组的末尾。经过多轮迭代,整个数组会变得有序。 二…...

windows11下git与 openssl要注意的问题
看了一下自己贴文的历史,有一条重要的忘了写了。 当时帮有位同事配置gitlab,众说周知gitlab是不太好操作。 但我还是自认自己git还是相当熟的。 解决了一系列问题,如配置代理,sshkey,私有库,等等࿰…...

lua除法bug
故事背景,新来了一个数值,要改公式。神奇的一幕出现了,公式算出一个非常大的数。排查是lua有一个除法bug,1除以大数得到一个非常大的数。 function div(a, b)return tonumber(string.format("%.2f", a/b)) end print(1/73003) pri…...

Ubuntu下Docker容器java服务往mysql插入中文数据乱码
一、问题描述 1、java服务部署在ubuntu下的docker容器内,但是会出现部分插入中文数据显示乱码,如图所示: 二、解决方案 1、查看mysql是否支持utf8,登录进入Mysql 输入命令: mysql -u root -pshow variables like c…...

C语言根据字符串变量获取/设置结构体成员值
一、背景 在项目中需要根据从数据库中获取的字段与对应的键值付给对应结构体成员上,而c语言中没有类似的反射机制,所以需要实现类似功能。例,从表中查到a 10,在结构体t中,需要将 t.a 10。 二、实现 感谢ChatGPT&…...

Selenium 自动化测试demo
场景描述: 模拟用户登录页面操作,包括输入用户名、密码、验证码。验证码为算数运算,如下: 使用到的工具和依赖: 1. Selenium:pip install selenium 2. 需要安装浏览器驱动:这里使用的是Edge 3…...

LeetCode 111.二叉树的最小深度
题目: 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明:叶子节点是指没有子节点的节点。 思路:自底向上(归)/自顶向下(递) DF…...

大工C语言作业答案
前言 这里是大连理工大学新版C语言课程MOOC作业的答案。 后期我会把全部的作业答案开源出来,希望对大家有帮助。 第九周第一题 #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> int B(int i) {int sum 1;while (i > 0){sum i * sum;i--;}return su…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
