数据结构_图的应用
最小生成树
Prim算法

int AMGraph::sum(string v)
{int start, totalW, cnt, minW, u, vv, i, j;start = LocateVex(v); // 获取起始顶点编号memset(visited, false, sizeof(visited)); // 初始化访问状态visited[start] = true;totalW = 0; // 最小生成树的总权重cnt = 1; // 当前生成树包含的顶点数while (cnt < vexnum){minW = INT_MAX; // 当前最小边权值u = -1; // 最小边的两个端点vv = -1;for (i = 0; i < vexnum; i++){// 遍历已加入生成树的顶点if (visited[i]){for (j = 0; j < vexnum; j++){if (!visited[j] && arcs[i][j] < minW){minW = arcs[i][j];u = i; // 起始点vv = j; // 终点}}}}// 无法继续扩展生成树if (vv == -1){break;}visited[vv] = true; // 将v加入生成树totalW += minW; // 累加权值cnt++; // 增加生成树的顶点计数}return totalW;
}
Kruskal算法

void AMGraph::kruskal()
{int i, j;for (i = 0; i < arcnum; i++) // 将所有的边按照从小到大排序{for (j = i + 1; j < arcnum; j++){if ((edges[i].w > edges[j].w) || (edges[i].w == edges[j].w && edges[i].u > edges[j].u)){Edge temp = edges[i];edges[i] = edges[j];edges[j] = temp;}}}for (i = 0; i < vexnum; i++) // 初始化{Vexset[i] = i;}for (i = 0; i < arcnum; i++) // 遍历所有的边{int v1 = edges[i].u; // 边的始点的下标int v2 = edges[i].v; // 边的终点的下标int vs1 = Vexset[v1]; // 连通分量int vs2 = Vexset[v2];// 如果两个节点不在同一棵树中,说明这条边可以添加到最小生成树中if (vs1 != vs2){if (edges[i].u < edges[i].v){cout << vexs[edges[i].u] << " " << vexs[edges[i].v] << " " << edges[i].w << endl;}else{cout << vexs[edges[i].v] << " " << vexs[edges[i].u] << " " << edges[i].w << endl;}// 合并两个分量for (j = 0; j < arcnum; j++){if (Vexset[j] == vs2){Vexset[j] = vs1;}}}}
}
两种算法比较

最短路径
Dijkstra算法


#include <iostream>
#include <climits>
#include <algorithm>
#include <string>
using namespace std;const int MaxLen = 100; // 设定图最多包含顶点class Map
{
private:string vexsU[MaxLen]; // 顶点表bool visited[MaxLen]; // 访问标志数组int Maxtrix[MaxLen][MaxLen]; // 图的邻接矩阵int Vexnum; // 图的顶点个数int dist[MaxLen]; // 存储源点到每个节点的最短距离int path[MaxLen]; // 用于存储每个顶点的前驱节点
public:void SetMatrix(int vnum, int mx[MaxLen][MaxLen], string vexs[MaxLen]);void Dijkstra(int n, string s);int LocateVex(string u);void PrintPath(int start, int end); // 打印从 start 到 end 的路径
};// 设置邻接矩阵和顶点表
void Map::SetMatrix(int vnum, int mx[MaxLen][MaxLen], string vexs[MaxLen])
{Vexnum = vnum;for (int i = 0; i < vnum; i++){vexsU[i] = vexs[i]; // 初始化顶点表for (int j = 0; j < vnum; j++){Maxtrix[i][j] = mx[i][j];}}
}// 打印路径
void Map::PrintPath(int start, int end)
{if (start == end){cout << vexsU[start];return;}if (path[end] == -1){cout << "无路径";return;}PrintPath(start, path[end]);cout << " " << vexsU[end];
}// 迪杰斯特拉算法
void Map::Dijkstra(int n, string s)
{// 初始化距离数组、访问数组和路径数组for (int i = 0; i < n; i++){dist[i] = INT_MAX;visited[i] = false;path[i] = -1; // -1 表示无前驱}int start = LocateVex(s);dist[start] = 0; // 起点到自身的距离为 0for (int i = 0; i < n; i++){int u = -1;// 从未访问的节点中找到距离最近的节点 ufor (int j = 0; j < n; j++){if (!visited[j] && (u == -1 || dist[j] < dist[u])){u = j;}}if (u == -1 || dist[u] == INT_MAX){break; // 剩余节点不可达}visited[u] = true; // 标记该节点为已访问// 更新所有与 u 相邻的节点的距离for (int v = 0; v < n; v++){if (Maxtrix[u][v] != INT_MAX && dist[u] + Maxtrix[u][v] < dist[v]){dist[v] = dist[u] + Maxtrix[u][v];path[v] = u; // 更新前驱节点}}}// 输出最短路径for (int i = 1; i < n; i++){cout << vexsU[start] << "-" << vexsU[i] << "-";if (dist[i] == INT_MAX){cout << "-1" << endl; // 不可达}else{cout << dist[i] << "----[";PrintPath(start, i);cout << " ]" << endl;}}
}// 定位顶点索引
int Map::LocateVex(string u)
{for (int i = 0; i < Vexnum; i++){if (u == vexsU[i]){return i;}}return -1;
}int main()
{int t, n, i, j, Matrix[MaxLen][MaxLen];string vexs[MaxLen], start;cin >> t;while (t--){cin >> n; // 顶点数for (i = 0; i < n; i++){cin >> vexs[i]; // 输入每个顶点名称}for (i = 0; i < n; i++){for (j = 0; j < n; j++){cin >> Matrix[i][j];if (Matrix[i][j] == 0 && i != j){Matrix[i][j] = INT_MAX; // 没有边的情况}}}cin >> start;Map m;m.SetMatrix(n, Matrix, vexs);m.Dijkstra(n, start);}return 0;
}
Foyed算法

拓扑排序


// 求各顶点的入度
void Map::FindInDegree()
{int i, j;// 初始化for (i = 0; i < MaxLen; i++){indegree[i] = 0;}for (i = 0; i < Vexnum; i++){for (j = 0; j < Vexnum; j++){if (Maxtrix[i][j] == 1){indegree[j]++;}}}
}// 输出拓扑排序的结果
void Map::topo()
{int i, k, m, current;queue<int> q;FindInDegree(); // 求各顶点的入度for (i = 0; i < Vexnum; i++){// 入度为0者进栈if (indegree[i] == 0){q.push(i);}}m = 0; // 对输出顶点计数,初始为0while (!q.empty()){current = q.front();q.pop();tp[m] = current;m++;for (k = 0; k < Vexnum; k++){if (Maxtrix[current][k] == 1){indegree[k]--;if (indegree[k] == 0){q.push(k);}}}}if (m == Vexnum){for (i = 0; i < m; i++){cout << tp[i] << " ";}}cout << endl;
}
关键路径
相关文章:

数据结构_图的应用
最小生成树 Prim算法 int AMGraph::sum(string v) {int start, totalW, cnt, minW, u, vv, i, j;start LocateVex(v); // 获取起始顶点编号memset(visited, false, sizeof(visited)); // 初始化访问状态visited[start] true;totalW 0; // 最小生成树的总权重cnt 1; // 当前…...

C#中面试的常见问题002
1.wpf和Winfrom的区别 1. 技术基础 WPF:基于.NET Framework,使用XAML(可扩展应用程序标记语言)作为界面描述语言,支持矢量图形和高级布局。WinForms:基于.NET Framework,使用纯代码或拖放设计…...

快速理解微服务中Ribbon的概念
一.基本概念 1.在微服务架构中,Ribbon 是一个客户端负载均衡器,用于控制服务间的通信方式。 2.Ribbon 是一个开源的库,最早由 Netflix 开发,用于实现客户端负载均衡。 3.Ribbon 主要解决的是在微服务架构中,多个服务…...

K8S简介、使用教程
以下是关于 Kubernetes(通常缩写为 K8S)的简介和使用教程: 一、Kubernetes 简介 定义与作用 Kubernetes 是一个开源的容器编排平台,用于自动化部署、扩展和管理容器化应用程序。它最初由谷歌开发,后捐赠给云原生计算基…...

极狐GitLab 17.6 正式发布几十项与 DevSecOps 相关的功能【四】
GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 学习极狐GitLab 的相关资料: 极狐GitLab 官网极狐…...

麦肯锡报告 | 科技落地的真谛:超越技术本身的价值创造
科技创新正在以惊人的速度改变企业运作和客户体验,但实现其潜力的关键在于正确的策略、流程、文化和人才。麦肯锡强调了一个理念:Never just tech(不仅仅是技术)。这表明,成功的数字化转型不仅依赖于技术,还…...

彻底解决 macOS 下Matplotlib 中文显示乱码问题
彻底解决 macOS 下Matplotlib 中文显示乱码问题 在使用 Python 的 Matplotlib 库进行数据可视化时,中文字符的显示常常会出现乱码问题,尤其在 macOS 系统上。在网上找了一大堆方法,花了很久,发现不是要安装各种字体就是要改配置&…...

STM32-- keil 的option for target使用
keil版本号 1.device界面 如:stm32f103c8t6的工程,可以直接在device这里修改成stm32f103vct6,虽然引脚不一样,但是很多一样的地方,可以直接使用,有些不修改也可以下载程序。 2.target xtal的设置不起作用了…...

【MCU】微控制器的编程技术:ISP 与 IAP
在嵌入式领域中,将程序下载到内置 Flash 有两种技术 ISP (In-system programming) ISP 即在系统编程,是指一些可编程逻辑器件、微控制器、芯片组和其他嵌入式设备在安装到完整嵌入式系统后能够进行编程,而不需要在将芯片安装到系统中之前对…...

C#基础题总结
16.一张单据上有一个5位数的号码为6**42,其中百位数和千位数已模糊不清,但知道该数能被 57 和 67 除尽。设计一个算法,找出该单据所有可能的号码。 17.编程序求2~10000以内的完全数。一个数的因子(除了这个数本身&…...

Elasticsearch中的节点(比如共20个),其中的10个选了一个master,另外10个选了另一个master,怎么办?
大家好,我是锋哥。今天分享关于【Elasticsearch中的节点(比如共20个),其中的10个选了一个master,另外10个选了另一个master,怎么办?】面试题。希望对大家有帮助; Elasticsearch中的节…...

《参与中型项目,领略 Spring 魅力》
一、Spring 在中型项目中的魅力展现 Spring 框架以其强大的功能和灵活性,在中型项目中发挥着重要作用。它不仅简化了开发过程,还提高了代码的可维护性和可扩展性。 Spring 在中型项目中魅力十足,其优势主要体现在以下几个方面。 首先&#…...
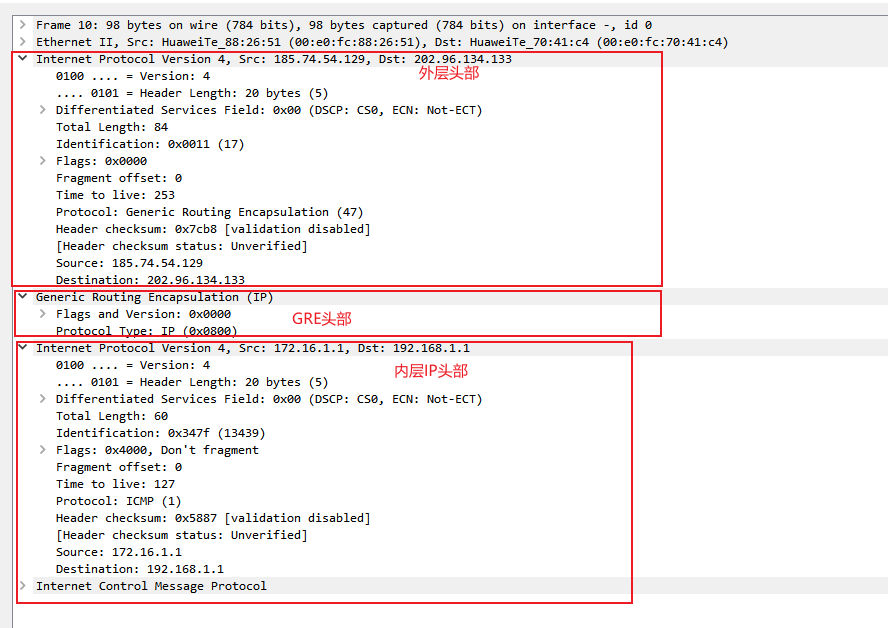
计算机网络-GRE(通用路由封装协议)简介
昨天我们学习了VPN的基本概念,虚拟专用网络在当前企业总部与分支间广泛使用。常用的划分方法为基于协议层次有GRE VPN、IPSec VPN、L2TP VPN、PPTP VPN、SSL VPN等。其实我有考虑该怎么讲,因为在IP阶段好像虚拟专用网络讲得不深,在IE的阶段会…...

开源电话机器人产品的优点是什么?
开源电话机器人产品的优点是什么? 作者:开源呼叫中心系统 FreeIPCC,Github地址:https://github.com/lihaiya/freeipcc 开源电话机器人产品作为人工智能技术的一种应用,近年来在电销、客户服务等多个领域展现出了显著的…...
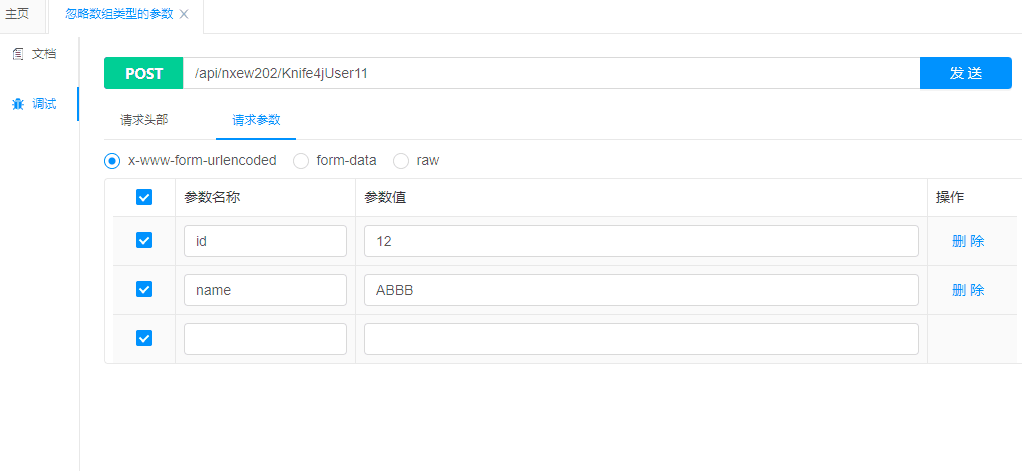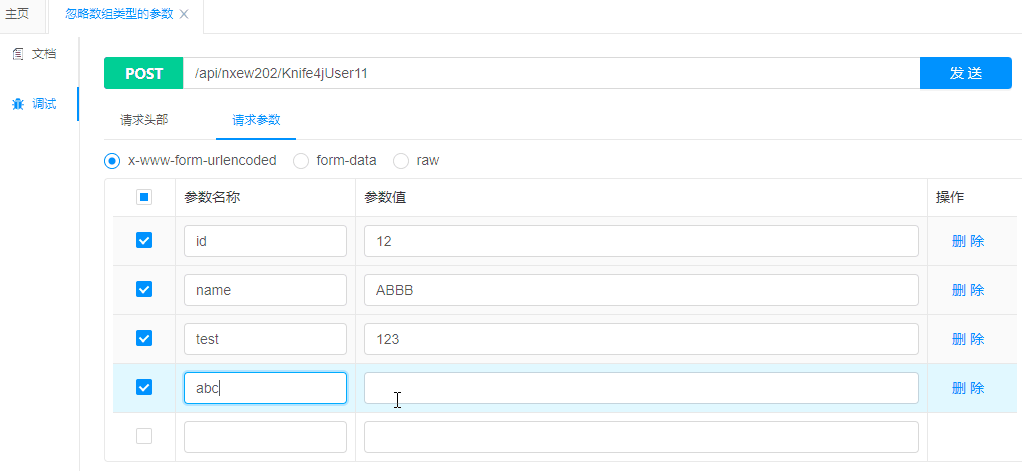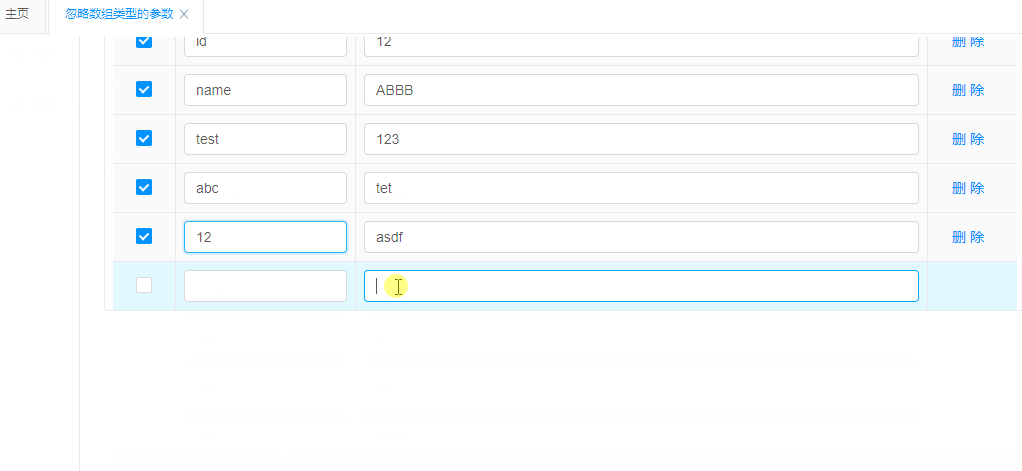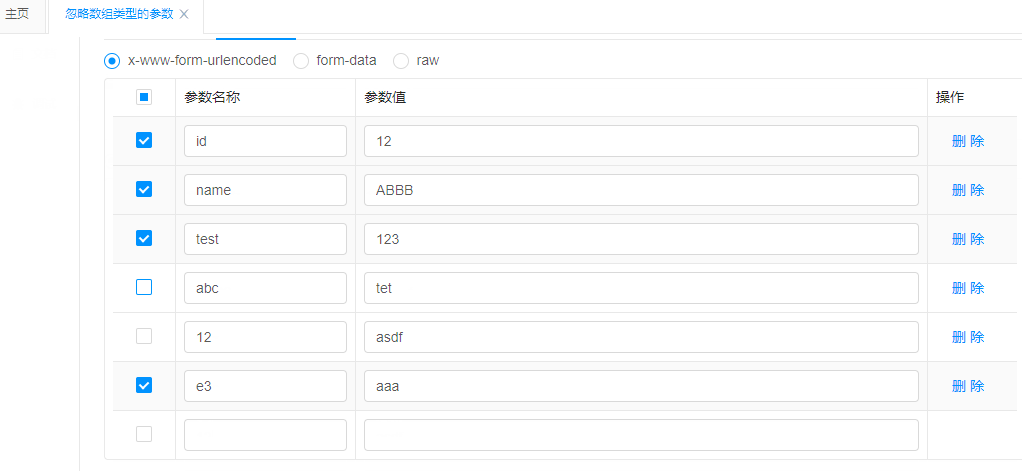
Spring Boot 集成 Knife4j 的 Swagger 文档
在开发微服务应用时,API 文档的生成和维护是非常重要的一环。Swagger 是一个非常流行的 API 文档工具,可以帮助我们自动生成 RESTful API 的文档,并提供了一个友好的界面供开发者测试 API。本文将介绍如何在 Spring Boot 项目中集成 Knife4j …...

极狐GitLab 17.6 正式发布几十项与 DevSecOps 相关的功能【一】
GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 学习极狐GitLab 的相关资料: 极狐GitLab 官网极狐…...

C# 在Word文档模板中,按照占位符插入文字或图片
1,引入包:DocX 2,代码如下 public class CC{public static void Ma22in(){// 示例:加载现有模板并替换占位符string templatePath "报告模板.docx"; // 模板文件路径string outputPath "Output.docx"; // 输出文…...

在使用PCA算法进行数据压缩降维时,如何确定最佳维度是一个关键问题?
一、PCA算法的基本原理 PCA算法的核心思想是通过正交变换,将一组可能相关的变量转换成一组线性不相关的变量,称为主成分。这组主成分能够以最小的信息损失来尽可能多地保留原始数据集的变异性。具体来说,PCA算法包括以下几个步骤:…...
深度学习3
五、自动微分 1、基础概念 模块 autograd 负责自动计算张量操作的梯度,具有自动求导功能;autograd 创建一个动态计算图来跟踪张量的操作,每个张量是计算图中的一个节点,节点之间的操作构成图的边。 属性 requires_grad 决定…...

Qt5.14.2的安装与环境变量及一些依赖库的配置
目录 1.Qt5.14.2安装 2.Qt环境变量及一些依赖库的配置 1.Qt5.14.2安装 QT从入门到入土(一)——Qt5.14.2安装教程和VS2019环境配置 - 唯有自己强大 - 博客园 2.Qt环境变量及一些依赖库的配置 假设QT安装目录为: D:\Qt\Qt5.14.2 将目录: D:\Qt\Qt5.14.…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
