STL算法之数值算法<stl_numeric.h>
这一节介绍的算法,统称为数值(numeric)算法。STL规定,欲使用它们,客户端必须包含头文件<numeric>.SGI将它们实现与<stl_numeric.h>文件中。
目录
运用实例
accumulate
adjacent_difference
inner_product
partial_sum
power
iota
运用实例
观察这些算法的源码之前,首先运行几个实例。
#include <numeric>
#include <vector>
#include <functional>
#include <iostream>
#include <iterator>
#include <algorithm>
using namespace std;int main() {int ia[5] = {1, 2, 3, 4, 5};vector<int> iv(ia, ia + 5);cout << accumulate(iv.begin(), iv.end(), 10) << endl;// 25, i.e. 10 + 1 + 2 + 3 + 4 + 5 cout << accumulate(iv.begin(), iv.end(), 25, minus<int>()) << endl;// 10, i.e. 25 - 1 - 2 - 3 - 4 - 5 注意25并没有执行minus<int>运算cout << inner_product(iv.begin() + 1, iv.end(), iv.begin(), 10) << endl;// 50, i.e. 10 + 2*1 + 3*2 + 4*3 + 5*4cout << inner_product(iv.begin() + 1, iv.end(), iv.begin(), 10, minus<int>(), plus<int>()) << endl;// -14, i.e. 10 - (2+1) - (3+2) - (4+3) - (5+4)cout << inner_product(iv.begin() + 1, iv.end(), iv.begin(), 10, minus<int>(), minus<int>()) << endl;// 6, i.e. 10 - (2-1) - (3-2) - (4-3) - (5-4)ostream_iterator<int> oite(cout, " ");partial_sum(iv.begin(), iv.end(), oite);// 1 3 6 10 15cout << endl;partial_sum(iv.begin(), iv.end(), oite, minus<int>());// 1 -1 -4 -8 -13cout << endl;adjacent_difference(iv.begin(), iv.end(), oite);// 1 1 1 1 1cout << endl;adjacent_difference(iv.begin(), iv.end(), oite, plus<int>());// 1 3 5 7 9cout << endl;int n = 3;iota (iv.begin(), iv.end() , n);for (int i =0; i < iv.size(); ++i) {cout << iv[i] << ' '; // 3 4 5 6 7}cout << endl;return 0;
}代码中的注释,标示了其运行结果;运行完这段代码,会对这几个数值算法有个基本的认识。
accumulate
template<class InputIterator, class T>
T accumulate(InputIterator first, InputIterator last, T init) {for (; first != last; ++first) init += *first;return init;
}template<class InputIterator, class T, class BinaryOperation>
T accumulate(InputIterator first, InputIterator last, T init, BinaryOperation binary_op) {for (; first != last; ++first) init = binary_op(init, *first);return init;
}算法accumulate用来计算init和[first,last)内所有元素的总和。注意,我们必须提供初始值init,这么做的原因之一是当[first,last)为空区间时,仍能获得一个明确定义的值。如果希望计算[first,last)中所有数值的总和,应该将init设为0.
式中的二元操作符不必满足交换律(commutative)和结合律(associative)。【如果需要将算法改造为可并行运算的算法,可能需要考虑结合律,暂不展开,后续博文进行尝试改造】
accumulate的行为顺序有明确的定义:现将init初始化,然后针对[first,last)区间中的每一个迭代器i,依次执行init = init + *i或者init=binary(init, *i)。
adjacent_difference
//版本一
template<class InputIterator, class OutputIterator>
OutputIterator adjacent_difference(InputIterator first, InputIterator last, OutputIterator result) {if (first == last) return result;*result = *first; // 首先记录第一个元素return __adjacent_difference(first, last, result, value_type(first));
}template<class InputIterator, class OutputIterator, class T>
OutputIterator __adjacent_difference(InputIterator first, InputIterator last, OutputIterator result, T*) {T value = *first;while(++first != last) {T tmp = *first;*++result = tmp - value;value = tmp;}return ++result;
}//版本二
template<class InputIterator, class OutputIterator, class BinaryOperator>
OutputIterator adjacent_difference(InputIterator first, InputIterator last, OutputIterator result, BinaryOperator binary_op ) {if (first == last) return result;*result = *first; // 首先记录第一个元素return __adjacent_difference(first, last, result, value_type(first), binary_op);
}template<class InputIterator, class OutputIterator, class T, class BinaryOperator>
OutputIterator __adjacent_difference(InputIterator first, InputIterator last, OutputIterator result, T*, BinaryOperator binary_op) {T value = *first;while(++first != last) {T tmp = *first;*++result = binary_op(tmp, value);value = tmp;}return ++result;
}
算法adjacent_difference用来计算[first, last)中相邻元素的差额。也就是说,它将*first赋给*result,并针对[first+1, last)内的每个迭代器i,将*i-*(i-1)之值赋给*(result+(i-first))。
注意,我们可以采用就地(inplace)运算方式,也就是另result等于first,在这种情况下,它是一个质变算法(mutating algorithm)。
"存储第一元素之值,然后存储后继元素之差值"这种做法很有用,因为这么一来便有足够的信息可以重建输入区间的原始内容。如果加法与减法定义如常规定义,那么adjacent_difference与partial_sum(稍后介绍)互为逆运算。这意思是,如果对区间1,2,3,4,5执行adjacent_difference,获得结果1,1,1,1,1,再对结果执行partial_sum便会获得原始区间1,2,3,4,5。
第一个版本使用operator-作为默认差额运算符,第二个版本采用外界提供的二元仿函数。第一个版本针对[first, last)中的每个迭代器i,将*i-*(i-1)赋值给*(resut+(i-first)),第二个版本则是将binary_op(*i, *(i-1))的运算结果赋值给*(result+(i-first))。
inner_product
//版本一
template<class InputIterator1, class InputIterator2, class T>
T inner_product(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, T init) {for (; first1 != last1; ++first1, ++first2)init += (*first1) * (*first2);return init;
}//版本二
template<class InputIterator1, class InputIterator2, class T, class BinaryOperator1, class BinaryOperator2>
T inner_product(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, T init, BinaryOperator1 binary_op1, BinaryOperator2 binary_op2) {for (; first1 != last1; ++first1, ++first2)init = binary_op1(init, binary_op2(*first1, *first2));return init;
}算法inner_product能够计算[first1,last1)和[first2, first2+ (last1-first1))的一般内积(generalized inner product)。注意,你一定得提供初值init。这么做的原因之一是当[first,last)为空时,仍可获得一个明确定义的结果。如果我们想计算两个vectors的一般内积,应该将init设为0.
第一个版本会将两个区间的内积结果加上init。也就是说,现将结果初始化为init,然后针对[first1, last1)的每一个迭代器i,有头到尾依序执行result=result+(*i)* *(first2+(i-first1))。
第二个版本与第一个版本唯一的差异是外界提供仿函数取代了operator+和operator*。也就是说,首先将结果初始化为init,然后针对[first1, last1)的每一个迭代器i,由头至尾执行result=binary_op1(result, binary_op2(*i, *(first2+(i-first1))))。
式中所用的二元仿函数不必满足交换律和结合律。inner_product所有运算的行为的顺序都有明确的设定。
partial_sum
//版本1
template <class InputIterator, class OutputIterator>
OutputIterator partial_sum(InputIterator first, InputIterator last, OutputIterator result) {if (first == last) return result;*result = *first;return __partial_sum(first, last, result, value_type(result));
}template <class InputIterator, class OutputIterator, class T>
OutputIterator __partial_sum(InputIterator first, InputIterator last, OutputIterator result, T*) {T value = *first;while(++first != last) {value = value + *first;*++result = value; }return ++result;
}//版本2
template <class InputIterator, class OutputIterator, class BinaryOperation>
OutputIterator partial_sum(InputIterator first, InputIterator last, OutputIterator result, BinaryOperation binary_op) {if (first == last) return result;*result = *first;return __partial_sum(first, last, result, value_type(result), binary_op);
}template <class InputIterator, class OutputIterator, class T, class BinaryOperation>
OutputIterator __partial_sum(InputIterator first, InputIterator last, OutputIterator result, T*, BinaryOperation binary_op) {T value = *first;while(++first != last) {value = binary_op(value, *first);*++result = value; }return ++result;
}算法partial_sum用来计算局部总和。他会将*frist赋值给*result,将*first和*(first+1)的和赋值给*(result+1),依次类推。注意,result可以等于first,这使得我们完成就地inplace计算。在这种情况下它是一个质变算法(mutating algorithm)。
运算中的总和首先初始化为*first,然后赋值给*result。对于[first,last)中每个迭代器i,从头至尾依次执行sum=sum+*i或者sum=binary_op(sum, *i),然后将sum赋值给*(result + (i-first))。
本算法返回输出区间的尾端result+(last-first)。
如果加法和减法的定义一如常规定义,那么partial_sum与先前介绍的adjacent_difference互为逆运算。(具体含义参见adjacent_difference那节的介绍)
power
这个算法是SGI专属,并不在STL标准之列。它用来计算某数的n幂次方。这个所谓的n幂次是指自己对自己进行某种运算,达到n次。运算类型可由外界指定;如果指定为乘法,那就是乘幂。
template<class T, class Integer>
inline T power(T x, Integer n) {return power(x, n, multiplies<T>());
}template<class T, class Integer, class MonoidOperation>
T power(T x, Integer n, MonoidOperation op) {if (n == 0) {return identity_element(op);} else {while ((n&1) == 0) {n >>= 1;x = op(x, x);}T result = x;n >> 1;while (n != 0) {x = op(x, x);if ((n & 1) !=0 ) {result = op(result, x);}n >> 1;}return result;}}iota
这个算法由SGI专属(clang++编译貌似可以通过),并不在STL标准之列。它用来设定某个区间的内容,使其的每一个元素从指定的value值开始,呈现递增状态。它改变了区间内容,所以是质变算法。
template<class ForwardIterator, class T>
void itoa(ForwardIterator first, ForwardIterator last, T value) {while(first != last) *first++ = value++;
}参考文档《STL源码剖析》--侯捷
相关文章:

STL算法之数值算法<stl_numeric.h>
这一节介绍的算法,统称为数值(numeric)算法。STL规定,欲使用它们,客户端必须包含头文件<numeric>.SGI将它们实现与<stl_numeric.h>文件中。 目录 运用实例 accumulate adjacent_difference inner_product partial_sum pow…...

Oracle如何记录登录用户IP
在运维场景中,在定位到某个SQL引起系统故障之后,想知道是哪台机器发过来的,方便定位源头,该如何解决? 在 Oracle 数据库中记录登录用户的 IP 地址可以通过多种方法实现。以下是几种常见的方法,包括使用触发…...

Python图像处理:打造平滑液化效果动画
液化动画中的强度变化是通过在每一帧中逐渐调整液化效果的强度参数来实现的。在提供的代码示例中,强度变化是通过一个简单的线性插值方法来控制的,即随着动画帧数的增加,液化效果的强度也逐渐增加。 def liquify_image(image, center, radius…...

构建Ceph分布式文件共享系统:手动部署指南
#作者:西门吹雪 文章目录 micro-Services-TutorialCeph分布式文件共享方案部署Ceph集群使用CephCeph在kubernetes集群中的使用 micro-Services-Tutorial 微服务最早由Martin Fowler与James Lewis于2014年共同提出,微服务架构风格是一种使用一套小服务来开发单个应…...

数据结构——用数组实现栈和队列
目录 用数组实现栈和队列 一、数组实现栈 1.stack类 2.测试 二、数组实现队列 1.Queue类 2.测试 查询——数组:数组在内存中是连续空间 增删改——链表:链表的增删改处理更方便一些 满足数据先进后出的特点的就是栈,先进先出就是队列…...

vue3typescript,shims-vue.d.ts中declare module的vue声明
webpack已经有了vue-loader这些loader了,为什么还需要declare module *.vue’呢? declare module 是为了告诉 tsc 这是一个“模块”。 如果不声明, IDE 里因为 tsc 类型检查, lint 会标红。 但vue-loader 是在 Webpack 构建阶段使…...
)
C/C++基础知识复习(30)
1) 什么是 C 中的 Lambda 表达式?它的作用是什么? Lambda 表达式: 在 C 中,Lambda 表达式是一种可以定义匿名函数的机制,可以在代码中快速创建一个内联的函数对象,而不需要显式地定义一个函数。Lambda 表…...

【NLP 1、人工智能与NLP简介】
人人都不看好你,可偏偏你最争气 —— 24.11.26 一、AI和NLP的基本介绍 1.人工智能发展流程 弱人工智能 ——> 强人工智能 ——> 超人工智能 ① 弱人工智能 人工智能算法只能在限定领域解决特定的问题 eg:特定场景下的文本分类、垂直领域下的对…...
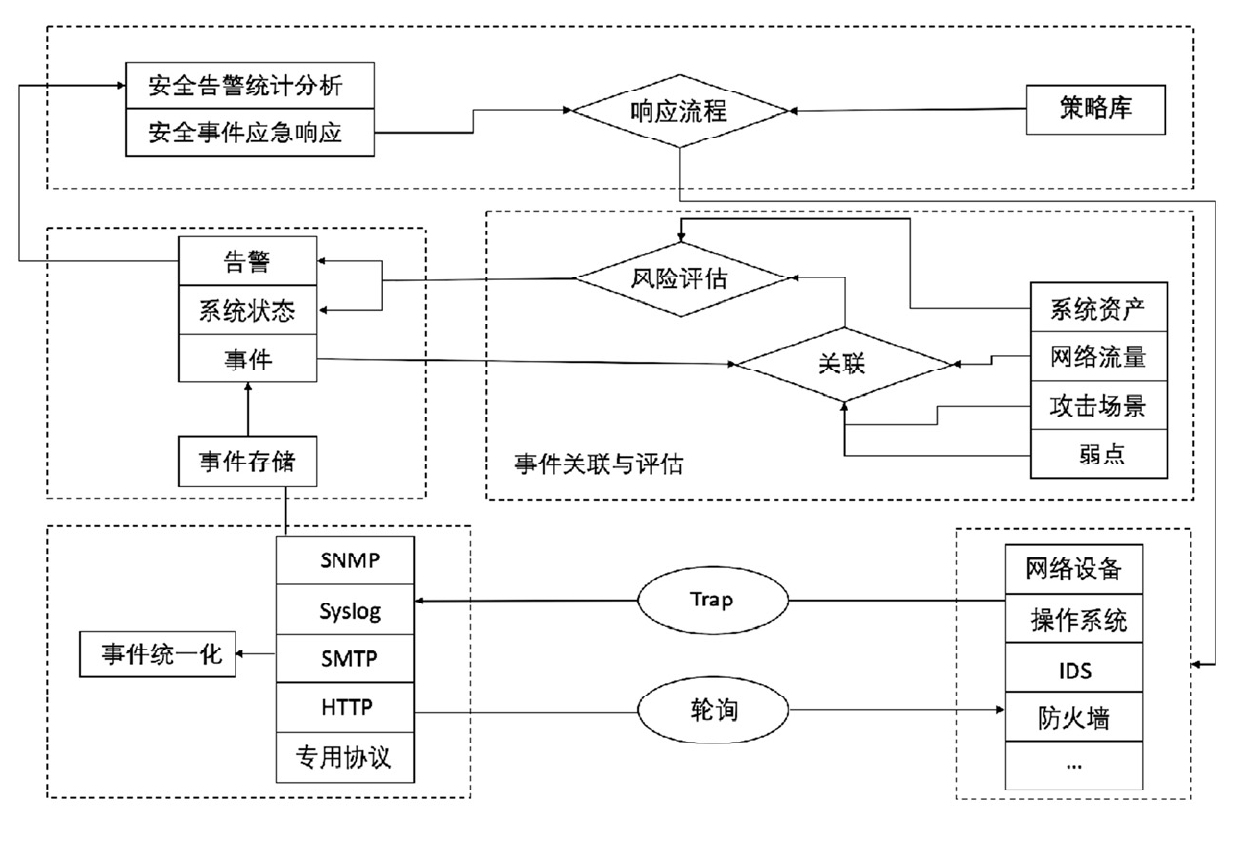
网络安全事件管理
一、背景 信息化技术的迅速发展已经极大地改变了人们的生活,网络安全威胁也日益多元化和复杂化。传统的网络安全防护手段难以应对当前繁杂的网络安全问题,构建主动防御的安全整体解决方案将更有利于防范未知的网络安全威胁。 国内外的安全事件在不断增…...

Swagger记录一次生成失败
最近在接入Swagger的时候遇到一个问题,就是Swagger UI可以使用的,但是/v3/docs 这个接口的json返回的base64类型的json,并不是纯json,后来检查之后是因为springboot3里面配置了json压缩。 Beanpublic HttpMessageConverters cusHt…...

Go 语言常用工具方法总结
在 Go 语言开发中,常常需要进行一些常见的类型转换、字符串处理、时间处理等操作。本文将总结一些常用的工具方法,帮助大家提高编码效率,并提供必要的代码解释和注意事项(go新人浅浅记录一下,以后来翻看🤣&…...

ThingsBoard规则链节点:GCP Pub/Sub 节点详解
目录 引言 1. GCP Pub/Sub 节点简介 2. 节点配置 2.1 基本配置示例 3. 使用场景 3.1 数据传输 3.2 数据分析 3.3 事件通知 3.4 任务调度 4. 实际项目中的应用 4.1 项目背景 4.2 项目需求 4.3 实现步骤 5. 总结 引言 ThingsBoard 是一个开源的物联网平台࿰…...

【Linux】select,poll和epoll
select,poll,epoll都是IO多路复用的机制。I/O多路复用就通过一种机制,可以监视多个描述符fd,一旦某个描述符就绪(一般是读就绪或者写就绪),系统会通知有I/O事件发生了(不能定位是哪一个)。但sel…...

Qt程序发布及打包成exe安装包
参考:Qt之程序发布以及打包成exe安装包 目录 一、简述 Qt 项目开发完成之后,需要打包发布程序,而因为用户电脑上没有 Qt 配置环境,所以需要将 release 生成的 exe 文件和所依赖的 dll 文件复制到一个文件夹中,然后再用 Inno Setup 打包工具打包成一个 exe 安装包,就可以…...

python怎样运行js语句
1. 安装 pip install PyExecJS # 需要注意, 包的名称:PyExecJS 2. 简单使用 import execjs execjs.eval("new Date") 返回值为: 2018-04-04T12:53:17.759Z execjs.eval("Date.now()") 返回值为:152284700108…...

汽车渲染领域:Blender 和 UE5 哪款更适用?两者区别?
在汽车渲染领域,选择合适的工具对于实现高质量的视觉效果至关重要。Blender和UE5(Unreal Engine 5)作为两大主流3D软件,各自在渲染动画方面有着显著的差异。本文将从核心定位与用途、工作流程、渲染技术和灵活性、后期处理与合成四…...

JAVA实现将PDF转换成word文档
POM.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.…...

前端-Git
一.基本概念 Git版本控制系统时一个分布式系统,是用来保存工程源代码历史状态的命令行工具 简单来说Git的作用就是版本管理工具。 Git的应用场景:多人开发管理代码;异地开发,版本管理,版本回滚。 Git 的三个区域&a…...

如何分析Windows防火墙日志
Windows防火墙,也被称为Windows Defender Firewall,是一种内置的安全功能,可以主动监控和分析运行Windows操作系统的计算机上通过Windows防火墙的网络流量,主要目的是作为计算机和互联网或其他网络之间的屏障,使管理员…...

工作坊报名|使用 TEN 与 Azure,探索你的多模态交互新场景
GPT-4o Realtime API 发布,语音 AI 技术正在进入一场新的爆发。语音AI技术的实时语音和视觉互动能力将为我们带来更多全新创意和应用场景。 实时音频交互: 允许应用程序实时接收并响应语音和文本输入。自然语音生成: 减少 AI 技术生成的语音…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
