算法笔记：滑动窗口

前言

滑动窗口作为一个考点较高的算法，广泛应用于子串问题中，本文将进行详细讲解。

一、滑动窗口是什么

滑动窗口是双指针算法的一种，基本思路为维护一个窗口，然后从前往后遍历元素进行运算。

二、滑动窗口算法和其他双指针算法的区别

双指针算法常见的为三种：
1.快慢指针算法（常用于链表有环判断）
2.双向指针（两个指针一个从最左，一个从最右出发进行查找），典型应用为二分查找
3.滑动窗口（两个指针一前一后出发，两个指针中间维持一个窗口结构

滑动窗口代码示例：

三、滑动窗口原理讲解

滑动：说明窗口不是固定不变的，而是具有一定的可变性的

窗口：窗口并不是一定固定不变的，可以进行扩大，然后逐步进行缩小直到满足情况

我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。

我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

流程图如下：

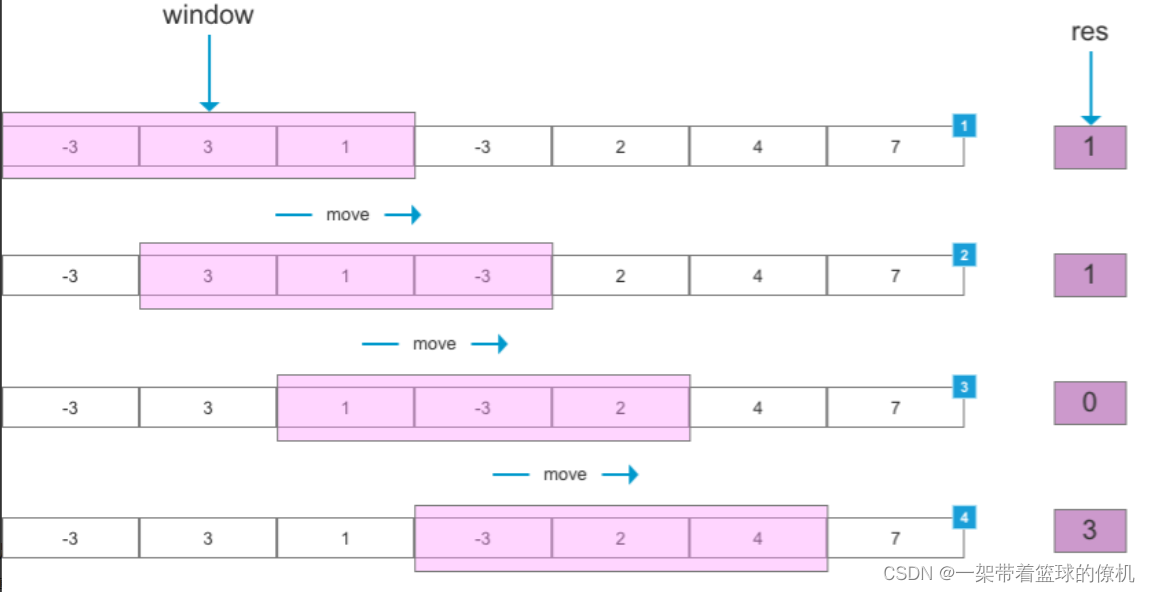
算法模版如下：

int left = 0, right = 0;while (right < s.size()) {// 增大窗口window.add(s[right]);right++;while (window needs shrink) {// 缩小窗口window.remove(s[left]);left++;}
}

四、例题讲解

3.无重复字符的最长子串

代码如下：

class Solution {public int lengthOfLongestSubstring(String s) {Set<Character> set =new HashSet<>();int max=0; //结果for(int right=0, left=0;right<s.length();right++){ //外层控制终点 也就是右边指针char ch=s.charAt(right); //right 右指针指向的就是当前需要考虑的元素while(set.contains(ch)){ //set中有重复元素 则缩短左边界 同时从set集合出元素set.remove(s.charAt(left)); //这一步是关键left++;}set.add(ch); //将当前元素加入max=Math.max(max,right-left+1); //计算当前不重复子串的长度}return max;}
}

思路：
首先定义一个Set集合用来存储当前的字符，max变量来保存最长的子序列结果，然后就是滑动窗口部分：
外层for循环控制终点，也就是right右指针， 里面一个while控制左指针，也就是左窗口，每当右指针移动一位时，取得当前的字符，查看是否已经添加到set集合中，如若没有就添加，继续移动右指针，如若发现已经存在，则移除该字符，将左指针向右移动一位，每次移动记录当前不重复子串长度，如若超过max值则赋值。

438. 找到字符串中所有字母异位词

思路：
将P转字符数组后排序成为判断的key，然后采用滑动窗口，定义左右指针，左指针指向s数组起始位置
右指针起始位置应该是目标p的长度-1，因为子串异位词肯定要和目标的长度是一致的，然后开始进行匹配，将子串同样进行排序转成key，如果能匹配，则代表是异位词，就将left左指针索引添加到结果中，如果不能匹配，就不加，匹配一次后，左右指针同时++，确保长度都是和目标字符长度一致。

代码：

class Solution {public List<Integer> findAnagrams(String s, String p) {char [] arr=p.toCharArray(); //先将目标字符串转为字符数组后 排序 组成keyArrays.sort(arr);String key=new String(arr); //字符数组转成keyHashSet<String> set=new HashSet<>();set.add(key); //将key添加进去int length=p.length();char [] target=new char[length]; //需要比对的子字段 长度应该和p的长度一致//   char [] strs=s.toCharArray();List<Integer> result=new ArrayList<>();for(int right=length-1,left=0;right<s.length();){ //外层循环 右指针 右窗口String   str =s.substring(left,right+1);// 减少移动次数 每次需要匹配目标字符对应长度的窗口 注意substring 的endinx是不包括 所以要+1target=str.toCharArray();Arrays.sort(target); //此时得到当前的 子串keyString son=new String(target);if(set.contains(son)){ //如果包含 则代表匹配 该子串是符合的异位词result.add(left); //将左指针也就是子串的起始索引添加至结果}right++;left++;//左右指针同时+1；}return result;}
}