动态系统特征分析:特征向量、特征值、频率与阻尼比、参与因子计算方法
特征值和特征向量在动态系统分析中是核心工具,广泛用于电力系统小信号稳定性、机械系统模态分析等领域。以下详细介绍计算方法及应用。
1. 求解特征值与特征向量
对于一个 n × n n\times n n×n的系统矩阵 A A A:
右特征向量与特征值
特征值( λ \lambda λ)及对应右特征向量( v \mathbf{v} v)满足以下特征方程:
A v = λ v A\mathbf{v}=\lambda\mathbf{v} Av=λv
常用数值计算工具:
- Python:
numpy.linalg.eig(A)得到特征值和右特征向量。 - MATLAB:
[V,D]=eig(A),其中 D D D为特征值对角矩阵, V V V为右特征向量矩阵。
左特征向量
左特征向量( u \mathbf{u} u)满足:
u T A = λ u T \mathbf{u}^T A=\lambda\mathbf{u}^T uTA=λuT
或等价于:
A T u = λ u A^T\mathbf{u}=\lambda\mathbf{u} ATu=λu
计算左特征向量可通过对 A T A^T AT求右特征向量实现。
左右特征向量的正交性
左特征向量 u i \mathbf{u}_i ui与右特征向量 v j \mathbf{v}_j vj之间满足正交性:
u i T v j = δ i j \mathbf{u}_i^T\mathbf{v}_j=\delta_{ij} uiTvj=δij
其中 δ i j \delta_{ij} δij为Kronecker delta。
2. 频率与阻尼比计算
假设特征值 λ \lambda λ为复数,表示为:
λ = σ + j ω \lambda=\sigma+j\omega λ=σ+jω
- 实部 σ \sigma σ为系统的衰减率;
- 虚部 ω \omega ω为振荡角频率。
频率计算
振荡频率 f f f:
f = ω 2 π f=\frac{\omega}{2\pi} f=2πω
阻尼比计算
阻尼比 ζ \zeta ζ定义为:
ζ = − σ σ 2 + ω 2 \zeta=-\frac{\sigma}{\sqrt{\sigma^2+\omega^2}} ζ=−σ2+ω2σ
- ζ > 1 \zeta>1 ζ>1:过阻尼系统(无振荡);
- ζ = 1 \zeta=1 ζ=1:临界阻尼系统;
- 0 < ζ < 1 0<\zeta<1 0<ζ<1:欠阻尼系统(伴随振荡);
- ζ = 0 \zeta=0 ζ=0:无阻尼(纯振荡);
- ζ < 0 \zeta<0 ζ<0:不稳定系统。
3. 示例代码
特征矩阵分析
对于一个复杂的矩阵 A A A:
A = [ 2 1 0 0 − 1 3 1 0 0 − 2 4 1 0 0 − 1 5 ] A = \begin{bmatrix} 2 & 1 & 0 & 0 \\ -1 & 3 & 1 & 0 \\ 0 & -2 & 4 & 1 \\ 0 & 0 & -1 & 5 \end{bmatrix} A= 2−10013−20014−10015
MATLAB代码
以下代码计算矩阵 A A A的特征值、左右特征向量、频率及阻尼比:
% 定义复杂的特征矩阵 A
A = [2, 1, 0, 0; -1, 3, 1, 0; 0, -2, 4, 1; 0, 0, -1, 5];% 求解特征值和右特征向量
[V, D] = eig(A); % V 为右特征向量,D 为特征值对角矩阵% 提取特征值
eigenvalues = diag(D);% 左特征向量(通过 A' 求解特征值和特征向量)
[U, ~] = eig(A'); % U 的列为左特征向量% 计算参与因子矩阵
Participation_Factors = abs(U' * V);% 计算频率和阻尼比
omega = imag(eigenvalues); % 振荡角频率
sigma = real(eigenvalues); % 衰减率
frequencies = omega / (2 * pi); % 振荡频率 (Hz)
damping_ratios = -sigma ./ abs(eigenvalues); % 阻尼比% 打印结果
disp('特征值:');
disp(eigenvalues);disp('右特征向量:');
disp(V);disp('左特征向量:');
disp(U);disp('频率 (Hz):');
disp(frequencies);disp('阻尼比:');
disp(damping_ratios);% 打印结果
disp('参与因子矩阵:');
disp(Participation_Factors);
特征值的预期结果
运行代码后,特征值可能为:
λ 1 = 5 , λ 2 = 4 + j , λ 3 = 4 − j , λ 4 = 2 \lambda_1 = 5, \quad \lambda_2 = 4 + j, \quad \lambda_3 = 4 - j, \quad \lambda_4 = 2 λ1=5,λ2=4+j,λ3=4−j,λ4=2
频率与阻尼比计算
- 对于复数特征值 λ = 4 ± j \lambda = 4 \pm j λ=4±j,频率:
f = ω 2 π = 1 2 π ≈ 0.159 Hz f = \frac{\omega}{2\pi} = \frac{1}{2\pi} \approx 0.159 \,\text{Hz} f=2πω=2π1≈0.159Hz
- 对应的阻尼比:
ζ = − σ σ 2 + ω 2 = − 4 4 2 + 1 2 = − 0.970 \zeta = -\frac{\sigma}{\sqrt{\sigma^2 + \omega^2}} = -\frac{4}{\sqrt{4^2 + 1^2}} = -0.970 ζ=−σ2+ω2σ=−42+124=−0.970
4. 应用场景
电力系统
在小信号稳定性分析中,通过特征值判断系统是否稳定。
机械系统
进行模态分析,利用频率和阻尼比评估振动特性。
控制系统
分析闭环系统的稳定性、响应速度及振荡行为。
相关文章:

动态系统特征分析:特征向量、特征值、频率与阻尼比、参与因子计算方法
特征值和特征向量在动态系统分析中是核心工具,广泛用于电力系统小信号稳定性、机械系统模态分析等领域。以下详细介绍计算方法及应用。 1. 求解特征值与特征向量 对于一个 n n n\times n nn的系统矩阵 A A A: 右特征向量与特征值 特征值( λ \lambd…...

乐鑫发布 esp-iot-solution v2.0 版本
今天,乐鑫很高兴地宣布,esp-iot-solution v2.0 版本已经发布,release/v2.0 分支下的正式版本组件将为用户提供为期两年的 Bugfix 维护(直到 2027.01.25 ESP-IDF v5.3 EOL)。该版本将物联网开发中常用的功能进行了分类整…...

动态代理如何加强安全性
在当今这个信息爆炸、网络无孔不入的时代,我们的每一次点击、每一次浏览都可能留下痕迹,成为潜在的安全隐患。如何在享受网络便利的同时,有效保护自己的隐私和信息安全,成为了每位网络使用者必须面对的重要课题。动态代理服务器&a…...

Flutter 之 InheritedWidget
InheritedWidget 是 Flutter 框架中的一个重要类,用于在 Widget 树中共享数据。它是 Flutter 中数据传递和状态管理的基础之一。通过 InheritedWidget,你可以让子 Widget 在不需要显式传递数据的情况下,访问祖先 Widget 中的数据。这种机制对…...

AI 助力开发新篇章:云开发 Copilot 深度体验与技术解析
本文 一、引言:技术浪潮中的个人视角1.1 AI 和低代码的崛起1.2 为什么选择云开发 Copilot? 二、云开发 Copilot 的核心功能解析2.1 自然语言驱动的低代码开发2.1.1 自然语言输入示例2.1.2 代码生成的模块化支持 2.2 实时预览与调整2.2.1 实时预览窗口功能…...

MyBatis-Plus介绍及基本使用
文章目录 概述介绍MyBatis-Plus 常用配置分页插件配置类注解配置 快速入门maven 依赖编写配置文件编写启动类编写 MybatisPlus 配置类 代码生成器:MybatisPlusGeneratormaven依赖代码生成器核心类 概述 介绍 MyBatis-Plus(简称 MP)是一个 M…...

SpringBoot 整合 Avro 与 Kafka
优质博文:IT-BLOG-CN 【需求】:生产者发送数据至 kafka 序列化使用 Avro,消费者通过 Avro 进行反序列化,并将数据通过 MyBatisPlus 存入数据库。 一、环境介绍 【1】Apache Avro 1.8;【2】Spring Kafka 1.2…...

支持JT1078和GB28181的流媒体服务器-LKM启动配置文件参数说明
流媒体服务器地址:https://github.com/lkmio/lkm GB28181信令,模拟多个国标设备工具:https://github.com/lkmio/gb-cms 文章目录 gop_cachegop_buffer_sizeprobe_timeoutwrite_timeoutmw_latencylisten_ippublic_ipidle_timeoutreceive_timeo…...
有哪些风险?)
什么是隐式类型转换?隐式类型转换可能带来哪些问题? 显式类型转换(如强制类型转换)有哪些风险?
C 中的隐式类型转换 定义:在 C 中,隐式类型转换是指由编译器自动执行的类型转换,不需要程序员显式地进行操作。这种转换在很多情况下会自动发生,比如在表达式求值、函数调用传参等过程中。常见场景 算术运算中的转换:…...
——金融研究者的得力助手)
量化交易新利器:阿布量化(AbuQuant)——金融研究者的得力助手
🚀 量化交易新利器:阿布量化(AbuQuant)——金融研究者的得力助手 🚀 文章目录 🚀 量化交易新利器:阿布量化(AbuQuant)——金融研究者的得力助手 🚀dz…...

UI设计从入门到进阶,全能实战课
课程内容: ├── 【宣导片】从入门到进阶!你的第一门UI必修课!.mp4 ├── 第0课:UI知识体系梳理 学习路径.mp4 ├── 第1课:IOS设计规范——基础规范与切图.mp4 ├── 第2课:IOS新趋势解析——模块规范与设计原则(上).mp4…...

Uniapp自动调整元素高度
获取设备的像素 如果你想让元素的高度相对于整个屏幕的高度占用一定的比例,可以通过获取屏幕的高度,然后计算出你想要的比例来设置元素的高度。以下是如何实现的示例: <script setup> import { ref, onMounted } from vue;// 定义一个…...

软考高项经验分享:我的备考之路与实战心得
软考,尤其是信息系统项目管理师(高项)考试,对于众多追求职业提升与专业认可的人士来说,是一场充满挑战与机遇的征程。我在当年参加软考高项的经历,可谓是一波三折,其中既有成功的喜悦࿰…...

安全关系型数据库查询新选择:Rust 语言的 rust-query 库深度解析
在当今这个数据驱动的时代,数据库作为信息存储和检索的核心组件,其重要性不言而喻。然而,对于开发者而言,如何在保证数据安全的前提下,高效地进行数据库操作却是一项挑战。传统的 SQL 查询虽然强大,但存在诸…...

《C++ 模型训练之早停法:有效预防过拟合的关键策略》
在 C 模型开发的复杂世界里,过拟合犹如一个潜藏的陷阱,常常使我们精心构建的模型在实际应用中表现大打折扣。而早停法(Early Stopping)作为一种行之有效的策略,能够帮助我们及时察觉模型训练过程中的异常,避…...

5.11【数据库】第一次实验
民宿预定,至少有不同的民宿,民宿下面有不同的房间(面积,房间编号) 房间类型,单价, 可预订以及不可预订 游客信息 订单信息 公司有很多课程, 学生,课程 每位学生每期…...

【CSS in Depth 2 精译_062】第 10 章 CSS 中的容器查询(@container)概述 + 10.1 容器查询的一个简单示例
当前内容所在位置(可进入专栏查看其他译好的章节内容) 【第十章 CSS 容器查询】 ✔️ 10.1 容器查询的一个简单示例 ✔️ 10.1.1 容器尺寸查询的用法 ✔️ 10.2 深入理解容器10.3 与容器相关的单位10.4 容器样式查询的用法10.5 本章小结 文章目录 第 10…...

蓝桥杯每日真题 - 第23天
题目:(直线) 题目描述(12届 C&C B组C题) 解题思路: 题目理解: 在平面直角坐标系中,从给定的点集中确定唯一的直线。 两点确定一条直线,判断两条直线是否相同,可通过…...

# Vue 入门级教程三
在前两篇 Vue 入门教程中,我们已经熟悉了 Vue 的基础语法、数据绑定、指令以及组件化开发等核心概念。在本教程中,我们将进一步探索 Vue 的高级特性,包括过滤器、自定义指令、过渡效果以及 Vue 与后端数据交互等内容,让你能够构建…...

hint: Updates were rejected because the tip of your current branch is behind!
问题 本地仓库往远段仓库推代码时候提示: error: failed to push some refs to 192.168.2.1:java-base/java-cloud.git hint: Updates were rejected because the tip of your current branch is behind! refs/heads/master:refs/heads/master [rejected] (…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
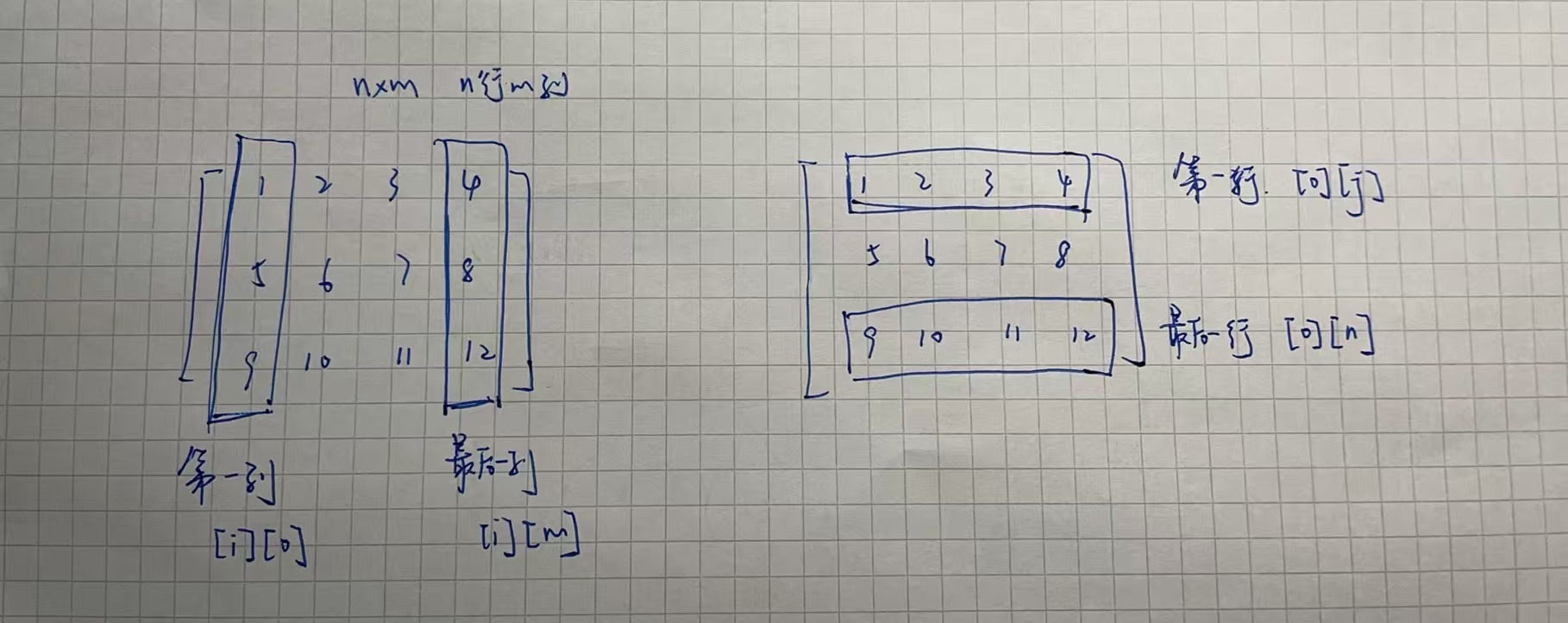
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...
