C/C++每日一练:合并K个有序链表
本篇博客将探讨如何 “合并K个有序链表” 这一经典问题。本文将从题目要求、解题思路、过程解析和相关知识点逐步展开,同时提供详细注释的代码示例。
链表(Linked List)
链表是一种线性数据结构,由一系列节点(Node)通过指针链接在一起。与数组不同,链表中的元素在内存中不需要连续存储,每个节点包含两部分:
- 数据部分:存储节点的值或数据。
- 指针部分:存储指向下一个节点的地址(单链表)或上一个和下一个节点的地址(双向链表)。
链表的类型主要有以下几种:
- 单链表:每个节点只指向下一个节点。
- 双向链表:每个节点既有指向下一个节点的指针,也有指向上一个节点的指针。
- 循环链表:链表的最后一个节点指向链表的头节点,形成循环。
链表的特点:
- 动态大小:可以根据需要动态地增加或减少元素,无需预分配存储空间。
- 插入/删除效率高:在链表的任意位置进行插入或删除操作只需修改指针,不涉及大量元素的移动,效率较高。
- 随机访问效率低:由于链表不支持直接访问任意位置的元素,需要通过遍历来查找特定位置的节点。
如下图所示:

题目要求
给定 k 个有序的链表,要求将它们合并成一个有序链表,并返回最终的结果链表。
输入
- 一个包含 k 个链表的数组,其中每个链表均已按升序排列。
输出
- 一个合并后的链表,且链表内元素按升序排列。
约束
k >= 1- 每个链表的长度可能不同,且长度总和不超过 10^5。
- 链表节点的值范围在 [-10^4, 10^4]。
解题思路
方法一:逐一合并
- 将所有链表两两合并。
- 时间复杂度为 O(k⋅n),其中 n 为平均每个链表的长度。
方法二:使用最小堆(优先队列)
- 利用最小堆维护每个链表当前节点的最小值,逐步提取并加入结果链表。
- 时间复杂度为 O(n⋅logk)。
方法三:分治合并
- 将 k 个链表两两分组合并。
- 类似归并排序,时间复杂度为 O(n⋅logk)。
以下主要以 方法二:使用最小堆 和 方法三:分治合并 为例进行解析。
过程解析
方法一:逐一合并
思路
将第一个链表作为初始结果链表,然后逐个将剩余的链表与当前结果链表进行合并,直到所有链表合并完毕。
实现步骤
- 初始化结果链表为第一个链表。
- 遍历链表数组,调用合并两个链表的函数,将当前链表与结果链表合并。
- 返回最终结果链表。
优点
- 实现简单,逻辑清晰,适合入门时使用。
缺点
- 效率较低,尤其在链表数量较多或链表长度较大时。
方法二:使用最小堆
思路
利用最小堆(优先队列)维护链表当前节点的最小值,每次从堆中提取最小值并将其加入结果链表,同时推进对应链表的指针。
实现步骤
- 创建一个最小堆,将所有链表的头节点加入堆中。
- 反复提取堆顶最小值,将其加入结果链表。
- 如果提取的节点有下一个节点,将下一个节点加入堆中。
- 堆为空时,所有节点已处理完,返回结果链表。
优点
- 在链表数量较多时表现优秀。
- 保证结果链表的构建是高效的。
缺点
- 实现稍复杂,需要熟悉堆的数据结构。
方法三:分治合并
思路
通过分治思想,将链表分成两组,递归地合并每组链表,直到最终只剩一个合并后的链表。
实现步骤
- 将链表数组两两分组,递归合并每组链表。
- 每次合并两个链表使用合并两个有序链表的逻辑。
- 最终返回唯一的合并链表。
优点
- 效率高,适合大规模链表数量。
- 思路清晰,类似归并排序的合并逻辑。
缺点
- 实现需要递归,可能在栈深度受限的系统中受到限制。
三种方法的比较
| 方法 | 时间复杂度 | 空间复杂度 | 适用场景 | 实现复杂度 |
|---|---|---|---|---|
| 逐一合并 | O(k⋅n)O(k \cdot n)O(k⋅n) | O(n)O(n)O(n) | 链表数量较少时 | 简单 |
| 使用最小堆 | O(n⋅logk)O(n \cdot \log k)O(n⋅logk) | O(k)O(k)O(k) | 链表数量较多时 | 中等 |
| 分治合并 | O(n⋅logk)O(n \cdot \log k)O(n⋅logk) | O(logk)O(\log k)O(logk) | 大规模链表合并 | 中等 |
- 如果链表数量很少,逐一合并的实现最简单,适合初学者练习。
- 如果链表数量较多且长度较短,最小堆法表现较优。
- 如果链表数量和长度都较多,分治合并法综合性能最好。
相关知识点
-
链表操作
- 基本操作:插入、删除、遍历。
- 注意指针的动态分配与释放。
-
优先队列
- C++ STL 中的std::priority_queue。
- 自定义排序方式。
-
分治策略
- 递归与归并思想。
示例代码
C代码实现:逐一合并
#include <stdio.h> // 包含标准输入输出头文件,提供 printf、scanf 等函数
#include <stdlib.h> // 包含动态内存分配和其他实用功能函数,如 malloc 和 free// 定义链表节点结构
typedef struct ListNode {int val; // 节点的值struct ListNode* next; // 指向下一个节点的指针
} ListNode;// 合并两个有序链表的函数
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {// 如果 l1 为空,直接返回 l2if (!l1) return l2;// 如果 l2 为空,直接返回 l1if (!l2) return l1;// 比较两个链表头节点的值,递归合并较小值的后续节点if (l1->val < l2->val) {l1->next = mergeTwoLists(l1->next, l2); // l1 较小,递归处理 l1->nextreturn l1; // 返回 l1 作为新的头节点} else {l2->next = mergeTwoLists(l1, l2->next); // l2 较小,递归处理 l2->nextreturn l2; // 返回 l2 作为新的头节点}
}// 合并 K 个有序链表的函数
ListNode* mergeKLists(ListNode** lists, int k) {// 如果链表数组为空,直接返回 NULLif (k == 0) return NULL;// 初始化结果链表为第一个链表ListNode* mergedList = lists[0];// 遍历链表数组,从第二个链表开始逐一合并for (int i = 1; i < k; ++i) {mergedList = mergeTwoLists(mergedList, lists[i]); // 合并当前结果链表和下一个链表}// 返回最终合并完成的结果链表return mergedList;
}// 辅助函数:打印链表
void printList(ListNode* head) {// 遍历链表,打印每个节点的值while (head) {printf("%d -> ", head->val); // 输出当前节点的值head = head->next; // 移动到下一个节点}printf("NULL\n"); // 链表结束后打印 NULL
}// 辅助函数:创建链表节点
ListNode* createNode(int val) {// 动态分配内存为新节点ListNode* node = (ListNode*)malloc(sizeof(ListNode));node->val = val; // 设置节点值node->next = NULL; // 初始化下一个节点指针为空return node; // 返回新节点的指针
}// 主函数测试
int main()
{// 构建测试链表 1:1 -> 4 -> 5ListNode* list1 = createNode(1);list1->next = createNode(4);list1->next->next = createNode(5);// 构建测试链表 2:1 -> 3 -> 4ListNode* list2 = createNode(1);list2->next = createNode(3);list2->next->next = createNode(4);// 构建测试链表 3:2 -> 6ListNode* list3 = createNode(2);list3->next = createNode(6);// 创建链表数组存储所有链表ListNode* lists[] = {list1, list2, list3};// 合并链表ListNode* mergedList = mergeKLists(lists, 3);// 输出结果链表printf("Merged List: ");printList(mergedList);return 0; // 程序正常结束
}
C代码实现:最小堆解法
示例代码
#include <stdio.h> // 包含标准输入输出头文件
#include <stdlib.h> // 包含动态内存分配函数// 定义链表节点结构
typedef struct ListNode {int val; // 节点值struct ListNode* next; // 指向下一个节点的指针
} ListNode;// 定义小顶堆结构
typedef struct MinHeap {ListNode** array; // 存储链表节点的指针数组int size; // 当前堆的大小int capacity; // 堆的容量
} MinHeap;// 创建小顶堆
MinHeap* createMinHeap(int capacity) {// 分配堆结构和数组的内存MinHeap* heap = (MinHeap*)malloc(sizeof(MinHeap));heap->array = (ListNode**)malloc(sizeof(ListNode*) * capacity);heap->size = 0; // 初始化堆的大小为 0heap->capacity = capacity; // 设置堆容量return heap; // 返回堆的指针
}// 交换两个链表节点的指针
void swap(ListNode** a, ListNode** b) {ListNode* temp = *a;*a = *b;*b = temp;
}// 堆化调整函数(维护堆的性质)
void heapify(MinHeap* heap, int i) {int smallest = i; // 假设当前节点为最小值int left = 2 * i + 1; // 左子节点索引int right = 2 * i + 2; // 右子节点索引// 如果左子节点更小,更新最小值索引if (left < heap->size && heap->array[left]->val < heap->array[smallest]->val)smallest = left;// 如果右子节点更小,更新最小值索引if (right < heap->size && heap->array[right]->val < heap->array[smallest]->val)smallest = right;// 如果最小值不是当前节点,交换并递归调整if (smallest != i) {swap(&heap->array[i], &heap->array[smallest]);heapify(heap, smallest);}
}// 将节点插入到堆中
void insertHeap(MinHeap* heap, ListNode* node) {// 将新节点放在堆末尾heap->array[heap->size++] = node;int i = heap->size - 1; // 当前节点的索引// 向上调整节点位置以维护堆的性质while (i && heap->array[(i - 1) / 2]->val > heap->array[i]->val) {swap(&heap->array[i], &heap->array[(i - 1) / 2]);i = (i - 1) / 2; // 移动到父节点}
}// 从堆中提取最小值节点
ListNode* extractMin(MinHeap* heap) {if (heap->size == 0) return NULL; // 堆为空时返回 NULL// 获取堆顶最小值ListNode* root = heap->array[0];// 将堆末尾的节点移到堆顶heap->array[0] = heap->array[--heap->size];// 调整堆以恢复堆的性质heapify(heap, 0);return root; // 返回提取的最小值节点
}// 合并 K 个有序链表的函数
ListNode* mergeKLists(ListNode** lists, int k) {// 创建最小堆MinHeap* heap = createMinHeap(k);// 将每个链表的头节点加入堆中for (int i = 0; i < k; ++i) {if (lists[i]) insertHeap(heap, lists[i]);}// 创建结果链表的哑节点(dummy 节点)ListNode dummy;ListNode* tail = &dummy; // 结果链表的尾部指针dummy.next = NULL;// 从堆中逐一提取最小值节点并加入结果链表while (heap->size > 0) {// 提取堆中的最小值节点ListNode* minNode = extractMin(heap);// 将最小值节点连接到结果链表tail->next = minNode;tail = tail->next; // 更新尾部指针// 如果提取的节点还有下一个节点,将其加入堆中if (minNode->next) insertHeap(heap, minNode->next);}// 释放堆的内存free(heap->array);free(heap);return dummy.next; // 返回结果链表的头节点
}// 辅助函数:打印链表
void printList(ListNode* head) {while (head) {printf("%d -> ", head->val); // 打印节点值head = head->next; // 移动到下一个节点}printf("NULL\n"); // 链表结束
}// 辅助函数:创建链表节点
ListNode* createNode(int val) {ListNode* node = (ListNode*)malloc(sizeof(ListNode)); // 分配内存node->val = val; // 设置节点值node->next = NULL; // 初始化下一个指针return node;
}// 主函数测试
int main()
{// 构建测试链表 1:1 -> 4 -> 5ListNode* list1 = createNode(1);list1->next = createNode(4);list1->next->next = createNode(5);// 构建测试链表 2:1 -> 3 -> 4ListNode* list2 = createNode(1);list2->next = createNode(3);list2->next->next = createNode(4);// 构建测试链表 3:2 -> 6ListNode* list3 = createNode(2);list3->next = createNode(6);// 创建链表数组ListNode* lists[] = {list1, list2, list3};// 合并链表ListNode* mergedList = mergeKLists(lists, 3);// 输出结果链表printf("Merged List: ");printList(mergedList);return 0; // 程序结束
}
补充
小顶堆性质
小顶堆(Min-Heap) 是一种完全二叉树,它具有以下性质:
堆的结构性质:
- 小顶堆是一棵完全二叉树,即树是从左到右逐层填满的,只有最后一层可能不满,但节点必须从左向右连续排列。
堆的值性质:
- 每个节点的值都小于或等于其子节点的值。
- 即:对于任意节点
i,有:
A[i] ≤ A[2i+1](左子节点值)
A[i] ≤ A[2i+2](右子节点值)由于这两个性质,堆的最小值始终存储在根节点(即数组的第一个位置)。
数组表示:堆可以使用数组表示,将完全二叉树的节点按层序遍历的顺序存储:
索引: 0 1 2 3 4 5
值: 10 15 20 30 40 25
在数组中,可以通过以下规则找到父子节点的关系:
- 父节点索引: parent(i) = (i−1) / 2
- 左子节点索引: left(i) = 2i+1
- 右子节点索引: right(i) = 2i+2
示例:一个满足小顶堆性质的完全二叉树:
10/ \15 20/ \ /30 40 25
heapify 函数的作用
void heapify(MinHeap* heap, int i);
- i: 要调整的节点在堆数组中的索引。
- heap: 表示一个小顶堆,包含节点数组和堆的大小。
heapify 函数是小顶堆的调整函数,用来维护堆的性质(即每个节点的值都不大于其子节点的值)。它的作用是:
- 从索引 i 开始,将子树调整为满足小顶堆性质。
- 如果某节点不满足小顶堆性质,则通过交换该节点和其较小子节点的值,并递归调整子树,直到整个堆满足小顶堆性质。
实现逻辑
- 假设当前节点的值是最小的(设索引为 smallest)。
- 比较当前节点和其左、右子节点的值:
- 如果左子节点更小,更新 smallest为左子节点索引。
- 如果右子节点更小,更新 smallest为右子节点索引。
- 如果 smallest 发生变化(当前节点不是最小值),交换当前节点和 smallest的值。
- 递归调用 heapify,确保调整后的子树也满足小顶堆性质。
示例说明
假设有以下堆数组,表示一个不完全满足小顶堆性质的堆:
索引: 0 1 2 3 4 5
值: 40 15 20 30 10 25
对应的堆结构:
40/ \15 20/ \ /30 10 25
调用 heapify(heap, 0)
- 当前节点:
40(索引 0)。 - 左子节点:
15(索引 1)。 - 右子节点:
20(索引 2)。 - 最小值为左子节点
15,交换40和15。
调整后堆数组:
索引: 0 1 2 3 4 5
值: 15 40 20 30 10 25
对应堆结构:
15/ \40 20/ \ /30 10 25
递归调用 heapify(heap, 1):
- 当前节点:
40(索引 1)。 - 左子节点:
30(索引 3)。 - 右子节点:
10(索引 4)。 - 最小值为右子节点
10,交换40和10。
调整后堆数组:
索引: 0 1 2 3 4 5
值: 15 10 20 30 40 25
对应堆结构:
15/ \10 20/ \ /30 40 25
heapify(heap, 4) 不再需要调整,因为 40 没有子节点。
最终堆数组:
索引: 0 1 2 3 4 5
值: 15 10 20 30 40 25
最终堆结构:
15/ \10 20/ \ /30 40 25
C++代码实现:分治解法
#include <stdio.h> // 包含标准输入输出头文件
#include <stdlib.h> // 包含动态内存分配函数// 定义链表节点结构
typedef struct ListNode {int val; // 节点值struct ListNode* next; // 指向下一个节点的指针
} ListNode;// 合并两个有序链表的函数
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {// 如果 l1 为空,直接返回 l2if (!l1) return l2;// 如果 l2 为空,直接返回 l1if (!l2) return l1;// 比较两个链表的头节点,选择较小值作为合并后链表的头节点if (l1->val < l2->val) {l1->next = mergeTwoLists(l1->next, l2); // 递归处理 l1->next 和 l2return l1; // 返回 l1 作为当前链表头} else {l2->next = mergeTwoLists(l1, l2->next); // 递归处理 l1 和 l2->nextreturn l2; // 返回 l2 作为当前链表头}
}// 分治法合并 K 个有序链表
ListNode* mergeKListsDivideAndConquer(ListNode** lists, int left, int right) {// 如果左边界等于右边界,表示只剩下一个链表if (left == right) return lists[left];// 如果左边界大于右边界,返回 NULLif (left > right) return NULL;// 计算中间位置int mid = left + (right - left) / 2;// 递归地合并左半部分链表ListNode* l1 = mergeKListsDivideAndConquer(lists, left, mid);// 递归地合并右半部分链表ListNode* l2 = mergeKListsDivideAndConquer(lists, mid + 1, right);// 合并左右两部分链表return mergeTwoLists(l1, l2);
}// 主函数入口,用于调用分治法合并链表
ListNode* mergeKLists(ListNode** lists, int k) {// 如果链表数组为空,直接返回 NULLif (k == 0) return NULL;// 调用分治法进行合并return mergeKListsDivideAndConquer(lists, 0, k - 1);
}// 辅助函数:打印链表
void printList(ListNode* head) {while (head) {printf("%d -> ", head->val); // 打印当前节点的值head = head->next; // 移动到下一个节点}printf("NULL\n"); // 链表结束
}// 辅助函数:创建链表节点
ListNode* createNode(int val) {ListNode* node = (ListNode*)malloc(sizeof(ListNode)); // 分配内存node->val = val; // 设置节点值node->next = NULL; // 初始化指针return node; // 返回新节点
}// 主函数测试
int main()
{// 构建测试链表 1:1 -> 4 -> 5ListNode* list1 = createNode(1);list1->next = createNode(4);list1->next->next = createNode(5);// 构建测试链表 2:1 -> 3 -> 4ListNode* list2 = createNode(1);list2->next = createNode(3);list2->next->next = createNode(4);// 构建测试链表 3:2 -> 6ListNode* list3 = createNode(2);list3->next = createNode(6);// 创建链表数组ListNode* lists[] = {list1, list2, list3};// 调用分治法合并链表ListNode* mergedList = mergeKLists(lists, 3);// 打印结果链表printf("Merged List: ");printList(mergedList);return 0; // 程序正常结束
}
相关文章:

C/C++每日一练:合并K个有序链表
本篇博客将探讨如何 “合并K个有序链表” 这一经典问题。本文将从题目要求、解题思路、过程解析和相关知识点逐步展开,同时提供详细注释的代码示例。 链表(Linked List) 链表是一种线性数据结构,由一系列节点(Node&…...

STM32实现HC595控制三位数码管(内含程序,PCB原理图及相关资料)
目录 任务要求 一、595的作用 二、电路设计 三、STM32选型 四、cubeMX配置 五、代码实现 六、实现效果(显示12.8) 任务要求 使用两个595实现对三位数码管控制,实现三位值显示。 一、595的作用 74HC595的作用是将串行数据进行并行显示…...

《沉积与特提斯地质》
《沉积与特提斯地质》为中国地质调查局主管,中国地质调查局成都地质调查中心(西南地质科技创新中心)主办的地学类学术期刊。 《沉积与特提斯地质》创刊于1981年,创刊名为《岩相古地理研究与编图通讯》,后更名为《岩相…...

Android studio 签名加固后的apk文件
Android studio打包时,可以选择签名类型v1和v2,但是在经过加固后,签名就不在了,或者只有v1签名,这样是不安全的。 操作流程: 1、Android studio 对项目进行打包,生成有签名的apk文件ÿ…...
:项目集成方式详解——npm、cdn、下载、源码构建)
Brain.js(二):项目集成方式详解——npm、cdn、下载、源码构建
Brain.js 是一个强大且易用的 JavaScript 神经网络库,适用于前端和 Node.js 环境,帮助开发者轻松实现机器学习功能。 在前文Brain.js(一):可以在浏览器运行的、默认GPU加速的神经网络库概要介绍-发展历程和使用场景中&…...

关于Vscode配置Unity环境时的一些报错问题(持续更新)
第一种报错: 下载net请求超时(一般都会超时很正常的) 实际时并不需要解决,它对你的项目毫无影响 第二种报错: .net版本不匹配 解决:(由于造成问题不一样,所以建议都尝试一次&…...

MacOS 配置github密钥
MacOS 配置github密钥 1. 生成GitHub的SSH密钥对 ssh-keygen -t ed25519 -C "xxxxxxx.com" -f ~/.ssh/id_ed25519_github 其中 xxxxxxxxxxx.com 是注册github、gitee和gitlab的绑定账号的邮箱 -t ed25519:生成密钥的算法为ed25519(ed25519比rsa速度快&…...

从0开始学PHP面向对象内容之常用设计模式(策略,观察者)
PHP设计模式——行为型模式 PHP 设计模式中的行为模式(Behavioral Patterns)主要关注对象之间的通信和交互。行为模式的目的是在不暴露对象之间的具体通信细节的情况下,定义对象的行为和职责。它们常用于解决对象如何协调工作的问题ÿ…...

前端 如何用 div 标签实现 步骤审批
在前端实现一个步骤审批流程,通常是通过 div 标签和 CSS 来构建一个可视化的流程图,结合 JavaScript 控制审批的状态变化。你可以使用 div 标签创建每一个步骤节点,通过不同的样式(如颜色、边框等)表示审批的不同状态&…...

【大数据技术基础 | 实验十四】Kafka实验:订阅推送示例
文章目录 一、实验目的二、实验要求三、实验原理(一)Kafka简介(二)Kafka使用场景 四、实验环境五、实验内容和步骤(一)配置各服务器之间的免密登录(二)安装ZooKeeper集群(…...

SpringAi整合大模型(进阶版)
进阶版是在基础的对话版之上进行新增功能。 如果还没弄出基础版的,请参考 https://blog.csdn.net/weixin_54925172/article/details/144143523?sharetypeblogdetail&sharerId144143523&sharereferPC&sharesourceweixin_54925172&spm1011.2480.30…...

为什么爱用低秩矩阵
目录 为什么爱用低秩矩阵 一、定义与性质 二、区别与例子 为什么爱用低秩矩阵 我们更多地提及低秩分解而非满秩分解,主要是因为低秩分解在数据压缩、噪声去除、模型简化和特征提取等方面具有显著的优势。而满秩分解虽然能够保持数据的完整性,但在实际应用中的场景较为有限…...

React 自定义钩子:useOnlineStatus
我们今天的重点是 “useOnlineStatus” 钩子,这是 React 自定义钩子集合中众多精心制作的钩子之一。 Github 的:https://github.com/sergeyleschev/react-custom-hooks import { useState } from "react" import useEventListener from &quo…...

uniapp 小程序 监听全局路由跳转 获取路由参数
uniapp 小程序 监听全局路由跳转 获取路由参数 app.vue中 api文档 onLaunch: function(options) {let that this;let event [navigateTo, redirectTo, switchTab, navigateBack];event.forEach(item > {uni.addInterceptor(item, { //监听跳转//监听跳转success(e) {tha…...

12.02 深度学习-卷积
# 卷积 是用于图像处理 能够保存图像的一些特征 卷积层 如果用全连接神经网络处理图像 计算价格太大了 图像也被转为线性的对象导致失去了图像的空间特征 只有在卷积神经网络cnn的最后一层使用全连接神经网络 # 图像处理的三大任务 # 目标检测 对图像中的目标进行框出来 # 图…...

MySQL 主从同步一致性详解
MySQL主从同步是一种数据复制技术,它允许数据从一个数据库服务器(主服务器)自动同步到一个或多个数据库服务器(从服务器)。这种技术主要用于实现读写分离、提升数据库性能、容灾恢复以及数据冗余备份等目的。下面将详细…...

Spring源码导入idea时gradle构建慢问题
当我们将spring源码导入到idea进行构建的时候,spring采用的是gradle进行构建,默认下注在依赖是从https://repo.maven.apache.org会特别慢,需要改为国内的镜像地址会加快速度。 将项目中build.gradle配置进行调整: repositories …...

Dockerfile 安装echarts插件给java提供服务
java调用echarts插件,生成图片保存到磁盘然后插入到pptx中报表。 Dockerfile文件内容: #基础镜像,如果本地仓库没有,会从远程仓库拉取 openjdk:8 FROM docker.io/centos:centos7 #暴露端口 EXPOSE 9311 # 避免centos 日志输出 …...

Springboot小知识(1):启动类与配置
一、启动类(引导类) 在通常情况下,你创建的Spring应用项目都会为你自动生成一个启动类,它是这个应用的起点。 在Spring Boot中,引导类(也称为启动类,通常是main方法所在的类)是整个…...

[CISCN 2019华东南]Web11
[CISCN 2019华东南]Web11 给了两个链接但是都无法访问 这里我们直接抓包试一下 我们插入X-Forwarded-For:127.0.0.1 发现可以修改了右上角的IP地址,从而可以进行注入 {$smarty.version} 查看版本号 if标签执行PHP命令 {if phpinfo()}{/if} 查看协议 {if system(…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...
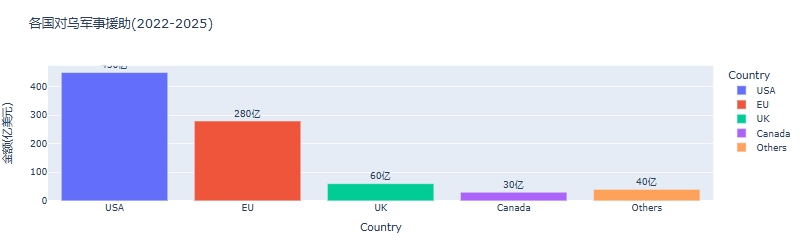
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
