算法分析与设计复习笔记
插入排序
1. void insert_sort(int A[ ],int n)
2. {
3. int a,i,j;
4. for (i=1;i<n;i++) {
5. a = A[ i ];
6. j = i – 1;
7. while (j>=0 && A[j]>a) {
8. A[ j+1 ] = A[ j ];
9. j- -;
10. }
11. A[ j+1 ] = a;
12. }
13. }
合并两个有序的子数组
1. void merge(int A[ ],int p,int q,int r)
2. {
3. int *bp = new int[r-p+1]; // 分配缓冲区,存放被排序的元素
4. int i,j,k;
5. i = p; j = q + 1; k = 0;
6. while (i<=q && j<=r) { // 逐一判断两子数组的元素
7. if (A[ i ] <=A[ j ]) // 按两种情况,把小的元素拷贝到
8. bp[ k++ ] = A[ i++ ]; // 缓冲区*/
9. else
10. bp[ k++ ] = A[ j++ ];
11. }
12. if (i==q+1) // 按两种情况,处理其余元素
13. for (;j<=r;j++)
14. bp[++] = A[j]; // 把A[ j ]~A[ r ]拷贝到缓冲区
15. else
16. for (;i<=q;i++)
17. bp[++] = A[i]; // 把A[i]~A[q]拷贝到缓冲区
18. k = 0;
19. for (i=p;i<=r;i++) // 最后,把数组bp的内容拷贝
20. A[i++] = bp[k++]; // 到 A[p]~A[r]
21. delete bp;
22. }
i:开始合并时第一个序列的起始位置
s:合并前序列的大小
t:合并后序列的大小
合并排序算法
1. template <class Type>
2. void merge_sort(Type A[ ],int n)
3. { int i, s, t = 1;
5. while (t<n) {
6. s = t; t = 2 * s; i = 0;
7. while (i+t<n) {
8. merge(A,i,i+s-1,i+t-1); //i,i+s-1,i+t-1定义被合并的两个序列的边界。
9. i = i + t;
10. }
11. if (i+s<n)
12. merge(A,i,i+s-1,n-1);
13. }
14. }
- 汉诺塔(Hanoi)问题:
void Hanoi (char a, char b, char c, int n)
{
if ( n ==1 ) printf (“%c->%c”, a, b);
else{
Hanoi( a, c, b, n-1);
printf( “%c->%c”, a, b);
Hanoi(c, b, a, n-1);
}
}
阶乘函数可归纳定义为:
 算法 计算阶乘函数 n!
算法 计算阶乘函数 n!
1. int factorial(int n)
2. {
3. if (n==0)
4. return 1;
5. else
6. return n * factorial(n-1);
7. }
整数划分问题
用一系列正整数之和的表达式来表示一个正整数,称为整数的划分。
例:7 可划分为:
7
6 + 1
5 + 2,5 + 1 + 1
4 + 3,4 + 2 + 1,4 + 1 + 1 + 1
3 + 3 + 1,3 + 2 + 2, 3 + 2 + 1 + 1,3 + 1 + 1 + 1 + 1
2 + 2 + 2 + 1,2 + 2 + 1 + 1 + 1,2 + 1 + 1 + 1+ 1 + 1
1 + 1 + 1+ 1 + 1 + 1 + 1
上述任何一个表达式都称为整数 7 的一个划分。
2)正整数 n 的不同的划分个数称为正整数 n 的划分数,记为 p(n );
3)求正整数 n 的划分数称为整数划分问题。
1)定义两个函数:
r(n,m):正整数 n 的划分中加数含 m 而不含大于 m 的所有划分数;
q(n,m):正整数 n 的划分中加数小于或等于 m 的所有划分数。
例:在 7 的划分中:
含 6 而不含大于 6 的划分有:
6 + 1,因此,r(7,6)=1;
含 5 而不含大于 5 的划分有:
5 + 2,5 + 1 + 1,因此,r(7,5)=2;
含 4 而不含大于 4 的划分有:
4 + 3,4 + 2 + 1,4 + 1 + 1 + 1,因此,r(7,4)=3;
含 3 而不含大于 3 的划分有:
3 + 3 + 1,3 + 2 + 2, 3 + 2 + 1 + 1,3 + 1 + 1 + 1 + 1
因此,r(7,3)=4
4)递归式:
⑴ 由式 (4.1.1) 和式 (4.1.2) 可得下面递归关系:
⑵ 对所有的正整数 n, 有:
⑶ n 的划分不可能包含大于 n 的加数
⑷ 整数 1 只有一个划分,而不管 m 有多大
⑸
分治策略
将要求解的较大规模问题分割成若干个更小规模的子问题;
对这些子问题分别求解,如果子问题的规模仍不够小,则再划分为更小的子问题,如此递归的进行下去,直到问题规模足够小、很容易求出其解为止。
将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解。
- 分治法所能解决的问题一般具有以下几个特征:
- 该问题的规模缩小到一定的程度就可以容易地解决;
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
- 利用该问题分解出的子问题的解可以合并为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
快速排序的序列的划分算法
2. int split(Type A[ ], int low, int high)
3. { int k, i = low;
5. Type x = A[low];
6. for (k=low+1; k<=high; k++) {
7. if (A[k]<=x) {
8. i = i + 1;
9. if (i!=k) swap(A[i], A[k]);
11. }
12. }
13. swap(A[low], A[i]);
14. return i;
15. }
快速排序:
1. template <class Type>
2. void quick_sort(Type A[ ], int low, int high)
3. {
4. int k;
5. if (low < high) {
6. k = split(A, low, high);
7. quick_sort(A, low, k-1); //对左半段排序
8. quick_sort(A, k+1, high); //对右半段排序
9. }
10. }
贪婪法:
解向量:问题中n个元素的具体取值所构成的向量;
解空间:问题中n个元素的各种不同取值组合所构成的向量全体;
约束方程:问题中的限制条件所列出的方程;
目标函数:问题求解所要达到的目标;
可行解:满足约束方程的向量;
最优解:使目标函数达极值的向量。
性质: 最优子结构性质(动态规划也有该性质) 自顶向下

斐波那契

分治法: 优化原则或最优子结构性质, 自底向上, 划分子问题
- 分治法所能解决的问题一般具有以下几个特征:
- 该问题的规模缩小到一定的程度就可以容易地解决;
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
- 利用该问题分解出的子问题的解可以合并为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
货郎担的动态规划函数

多段图动态规划函数:
 资源分配问题
资源分配问题

- 回溯法
- 回溯法是一个既带有系统性又带有跳跃性的搜索算法;
- 它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。——系统性
相关文章:

算法分析与设计复习笔记
插入排序 1. void insert_sort(int A[ ],int n) 2. { 3. int a,i,j; 4. for (i1;i<n;i) { 5. a A[ i ]; 6. j i – 1; 7. while (j>0 && A[j]>a) { 8. A[ j…...

vue-amap 高德地图
vue-amap是一套基于Vue 2/vue3和高德地图的地图组件 vue-amap 高德地图2.0版本的对应vue3...

Numpy基础练习
import numpy as np 1.创建一个长度为10的一维全为0的ndarray对象,然后让第5个元素等于1 n np.zeros(10,dtypenp.int32) n[4] 12.创建一个元素从10到49的ndarray对象 n np.arrange(10,50)3.将第2题的所有元素位置反转 n[::-1]使用np.random.random创建一个10*10的ndarray对象…...

一番赏小程序定制开发,打造全新抽赏体验平台
随着盲盒的热潮来袭,作为传统的潮玩方式一番赏也再次受到了大家的关注,市场热度不断上升! 一番赏能够让玩家百分百中奖,商品种类丰富、收藏价值高,拥有各种IP,从而吸引着各个圈子的粉丝玩家,用…...

【前端】将vue的方法挂载到window上供全局使用,也方便跟原生js做交互
【前端】将vue的方法挂载到window上供全局使用,也方便跟原生js做交互 <template><div><el-button click"start">调用方法</el-button></div> </template> <script> // import { JScallbackProc } from ./JScal…...

Oracle查询优化:高效实现仅查询前10条记录的方法与实践
在 Oracle 中,实现仅查询前10条记录的四种方法 1. 使用 ROWNUM 查询 ROWNUM 是 Oracle 中的伪列,用于限制返回的行数。 SELECT * FROM table_name WHERE condition AND ROWNUM < 10;condition:查询条件。ROWNUM < 10:限制…...

go语言编译问题
go编译 goproxy地址 阿里云 https://mirrors.aliyun.com/goproxy/七牛云 https://goproxy.cn/开源版 https://goproxy.io/nexus社区 https://gonexus.dev/启用 Go Modules 功能 go env -w GO111MODULEon配置 GOPROXY 环境变量,以下三选一 七牛 CDN go env -w …...

mobi文件转成pdf
将 MOBI 文件转换为 PDF 格式通常涉及两个步骤: 解析 MOBI 文件:需要提取 MOBI 文件的内容(文本、图片等)。将提取的内容转换为 PDF:将 MOBI 文件的内容渲染到 PDF 格式。 可用工具 kindleunpack 或 mobi࿱…...

MobaXterm解决中文显示乱码问题
1 问题 打开MobaXterm时,会显示中文乱码。 2 解决方法 右键点击会话,在弹出菜单中选择“编辑会话”,如下: 选择终端字体设置,如下: 字符集换成ISO-8859-1,如下: 网上有说用…...

西门子 SINAMICS G120 变频器借助 ProfiNet 转 EtherCAT 实现与汇川 H5U 通讯实例
一. 案例背景 随着智能制造理念的推进,设备之间的协同工作变得越来越重要。例如,在机器人自动化焊接生产线中,电机驱动的焊接机器人需要与其他设备协同工作,这就要求负责电机控制的变频器和控制整个生产线流程的PLC能…...
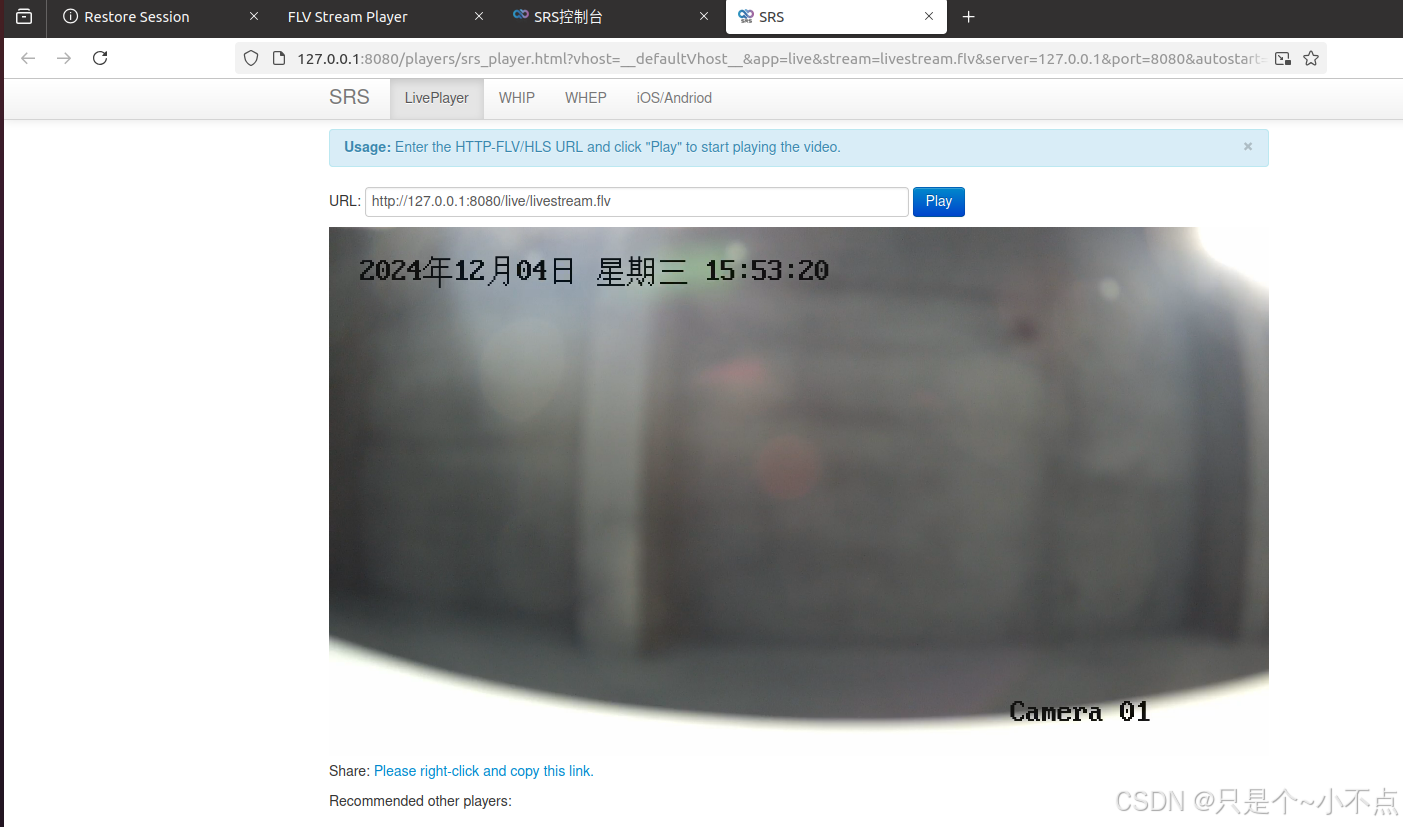
流媒体之linux下离线部署FFmpeg 和 SRS
前言 用户对网络做了限制,只能访问指定的网址,和没网没啥区别,导致无法连接外网,无法获取安装包,还有一些编译需要的开源工具 用户需要用平台查看库房的海康摄像头实时监控,只能在库房里一台纯净的ubantu…...

NOBLEROYCE罗慕路斯门窗 以精工匠造开启私属人生
公元前753年罗马建立,其创建者为罗慕路斯。以狼孩的传奇形象成为古罗马精神象征的罗慕路斯,不仅是罗马的第一任国王,还创建了罗马最初的政治制度,罗马的名字也是源于这位伟大的奠基人。NOBLEROYCE罗慕路斯,致敬这位人类…...

【算法day8】字符串:反转
主播今天脑子不好用,先写两题吧~ 题目引用 反转字符串中的单词右旋字符串 1.反转字符串 给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且…...

【C++进阶】第二节:多态
1、多态的概念 1.1 概念 多态的概念:通俗来说,就是多种形态。具体点就是去完成某个行为,当不同的对象去完成时会产生出不同的状态。 2、多态的定义及实现 2.1 多态的构成条件 多态是在不同继承关系的类对象,去调用同一函数&a…...

梯度下降法以及 Python 实现
文章目录 1. 引言2. 梯度法3. 例子4. 代码实现5. 讨论 — 学习率 η \eta η5.1 当 η \eta η 设置过大5.2 当 η \eta η 设置过小 参考 1. 引言 梯度下降法,可以根据微分求出的斜率计算函数的最小值。 在人工智能中,经常被应用于学习算法。 2. 梯…...

Postman cURL命令导入导出
你是否曾为在Postman和终端之间切换、整理请求而抓狂?其实,Postman支持与cURL命令的无缝互通,通过导入导出,极大提升效率。用好这个功能,分分钟让接口测试更高效! Postman如何快速导入cURL命令?…...

Java 在Json对象字符串中查找和提取特定的数据
1、在处理JSON数据时,需要提出个别字段的值,通过正则表达式提取特定的数据 public static void main(String[] args) {//定义多个JSON对象字符串类型,假设每个对象有a,b,c 字段String strJson "{\"a\":1.23,\"b\"…...

synchronized的特性
1.互斥 对于synchronized修饰的方法及代码块不同线程想同时进行访问就会互斥。 就比如synchronized修饰代码块时,一个线程进入该代码块就会进行“加锁”。 退出代码块时会进行“解锁”。 当其他线程想要访问被加锁的代码块时,就会阻塞等待。 阻塞等待…...

领域泛化与领域自适应
领域泛化(Domain Generalization)和领域适应(Domain Adaptation)是机器学习领域中处理不同数据分布场景下模型训练与应用的两种策略,领域泛化在泛化到目标领域时不需要进行调整,而领域自适应在适应到目标领…...

使用aspx,完成一个转发http的post请求功能的api接口,url中增加目标地址参数,传递自定义header参数
使用aspx,完成一个转发http的post请求功能的api接口,url中增加目标地址参数,传递自定义header参数 首先,简单实现一下,如何在ASPX页面中实现这个功能实现代码说明:注意事项: 然后进阶࿰…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
